Với lời giải SBT Toán 10 trang 100 Tập 1 chi tiết trong Bài 5: Tích của một số với một vectơ sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 5: Tích của một số với một vectơ
Bài 52 trang 100 SBT Toán 10 Tập 1: Cho tam giác ABC. Xác định các điểm M, N, P trong mỗi trường hợp sau:
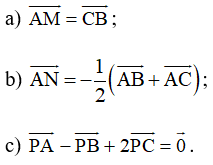
Lời giải:
a) Ta có:
⇒ AM // CB, AM = CB và M, B cùng phía so với bờ AC
⇒ ACBM là hình bình hành
Vậy điểm M thỏa mãn ACBM là hình bình hành.
b) Gọi N’ là trung điểm của BC
Khi đó ta có: hay
⇒
⇒ A là trung điểm của đoạn NN’
Vậy N là điểm đối xứng với N’ qua A.
c) Xét
⇔
⇔
⇒ Điểm P là điểm thỏa mãn PC // AB, P nằm cùng phía với A bờ BC sao cho 2PC = AB.
Vậy điểm P là điểm nằm trên đường thẳng song song với AB, nằm cùng phía với A so với BC sao cho 2PC = AB.
Bài 53 trang 100 SBT Toán 10 Tập 1: Cho tam giác ABC, kẻ tia phân giác AD. Đặt AB = b, AC = c. Chứng minh: .
Lời giải:
Xét tam giác ABC, có:
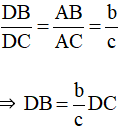
Ta có: D nằm giữa B và C nên và ngược hướng
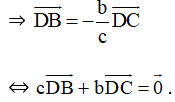
Bài 54* trang 100 SBT Toán 10 Tập 1: Cho hình bình hành ABCD. Lấy các điểm M, N, P thỏa mãn 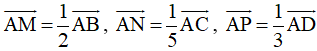 . Đặt và . Biểu thị các vec tơ
. Đặt và . Biểu thị các vec tơ ![]() theo các vectơ và . Chứng minh ba điểm M, N, P thẳng hàng.
theo các vectơ và . Chứng minh ba điểm M, N, P thẳng hàng.
Lời giải:
Ta có:
Ta có hay
Do đó M, N, P thẳng hàng.
Vậy ; ; và ba điểm M, N, P thẳng hàng.
Bài 55* trang 100 SBT Toán 10 Tập 1: Cho tam giác ABC. Lấy các điểm D, E, M, N thỏa mãn , , , với k là số thực. Đặt , . Biểu thị các vectơ , , theo các vectơ , và tìm k để ba điểm D, E, N thẳng hàng.
Lời giải:
Ta có:
= = .
Để ba điểm D, E, N thẳng hàng thì tồn tại t ∈ ℝ sao cho
⇔
⇔
⇔ ⇔
Do đó ba điểm D, E, N thẳng hàng khi k = .
Vậy , , và với k = thì ba điểm D, E, N thẳng hàng.
Bài 56* trang 100 SBT Toán 10 Tập 1: Cho tam giác ABC, lấy các điểm A’, B’, C’ không trùng với đỉnh của tam giác và lần lượt thuộc các cạnh AB, BC, CA thỏa mãn . Chứng minh hai tam giác ABC và A’B’C’ có cùng trọng tâm.
Lời giải:
Đặt (t > 0)
⇔
⇒ (vì các điểm A’, B’, C’ lần lượt thuộc các cạnh AB, BC, CA)
Gọi G là trọng tâm tam giác ABC nên
Ta có:
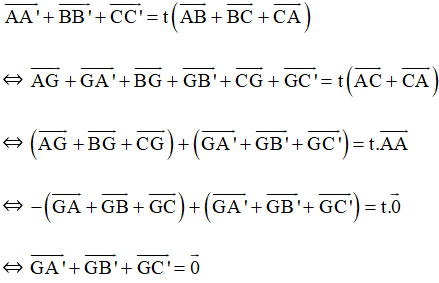
Suy ra G cũng là trọng tâm của tam giác A’B’C’.
Xem thêm các bài giải sách bài tập Toán 10 Cánh diều hay, chi tiết khác:
Giải SBT Toán 10 trang 99 Tập 1
Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:
Bài 4: Tổng và hiệu của hai vectơ
Bài 5: Tích của một số với một vectơ
Bài 6: Tích vô hướng của hai vectơ
Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây