Với giải sách bài tập Toán 10 Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây
Giải SBT Toán 10 trang 5 Tập 2
A. abc.
B. a + b + c.
C. 1.
D. ab + c.
Lời giải:
Đáp án đúng là B
Một công việc được hoàn thành bởi một trong ba hành động. Nếu hành động thứ nhất có a cách thực hiện, hành động thứ hai có b cách thực hiện, hành động thứ ba có c cách thực hiện (các cách thực hiện của ba hành động là khác nhau đôi một) thì công việc đó có a + b + c cách hoàn thành.
Vậy ta chọn phương án B.
A. abc.
B. a + b + c.
C. 1.
D. ab + c.
Lời giải:
Đáp án đúng là A
Một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có a cách thực hiện; ứng với mỗi cách thực hiện hành động thứ nhất, có b cách thực hiện hành động thứ hai; ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động thứ hai có c cách thực hiện hành động thứ ba thì công việc đó có a.b.c cách hoàn thành.
Vậy ta chọn phương án A.
Giải SBT Toán 10 trang 6 Tập 2
Lời giải:
Tổng số học sinh lớp 10A là: 10 + 25 = 35 (học sinh).
Nếu chọn một học sinh trong số 35 học sinh lớp 10A để làm lớp trưởng thì có 35 cách chọn.
Vậy có 35 cách chọn một bạn làm lớp trưởng lớp 10A.
Lời giải:
Tổng số quyển sách bạn Nam có là: 8 + 6 + 5 = 19 (quyển sách).
Nếu chọn một quyển sách trong số 19 quyển sách thì có 19 cách chọn.
Vậy bạn Nam có 19 cách chọn một quyển sách để đọc.
Lời giải:
Việc chọn hai điểm phân biệt trong số 20 điểm phân biệt để lập thành một vectơ là thực hiện hai hành động liên tiếp: chọn một điểm đầu tiên, sau đó chọn một điểm còn lại.
Có 20 cách chọn một điểm đầu tiên trong số 20 điểm phân biệt.
Vì ta đã chọn một điểm trên nên bây giờ ta chỉ còn 19 điểm phân biệt. Vì vậy lúc này có 19 cách chọn một điểm còn lại.
Vậy ta có thể lập được tất cả 20.19 = 380 vectơ khác từ 20 điểm đã cho.
Lời giải:
Ta thấy các chữ số của mỗi kí tự bạn Quân có thể lựa chọn là các số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Tức là có tổng cộng 10 số cho bạn Quân lựa chọn.
Việc chọn 3 kí tự cho dãy mật khẩu là thực hiện ba hành động liên tiếp: chọn số cho kí tự đầu tiên, sau đó chọn số cho kí tự thứ hai, cuối cùng là chọn số cho kí tự thứ ba.
Ở kí tự đầu tiên, bạn Quân có 10 cách chọn một số từ các số trên.
Tương tự như vậy, ở kí tự thứ hai, bạn Quân cũng có 10 cách chọn một số từ các số trên và ở kí tự thứ ba, bạn Quân cũng có 10 cách chọn một số từ các số trên.
Vậy bạn Quân có tất cả 10.10.10 = 103 = 1000 cách chọn dãy mật khẩu cho vali.
Bài 7 trang 6 SBT Toán 10 Tập 2: Lớp 10A có 30 học sinh. Giáo viên chủ nhiệm muốn chọn ban cán sự lớp gồm 3 thành viên: 1 lớp trưởng, 1 lớp phó học tập, 1 lớp phó văn thể. Hỏi giáo viên có bao nhiêu cách chọn một ban cán sự lớp?
Lời giải:
Việc chọn một ban cán sự lớp gồm 1 lớp trưởng, 1 lớp phó học tập và 1 lớp phó văn thể là thực hiện ba hành động liên tiếp: chọn 1 lớp trưởng, sau đó chọn 1 lớp phó học tập và cuối cùng chọn 1 lớp phó văn thể.
Vì lớp 10A có tất cả 30 học sinh nên có 30 cách chọn một lớp trưởng.
Vì giáo viên đã chọn một học sinh làm lớp trưởng nên lúc này ta có 29 cách chọn một lớp phó học tập.
Vì giáo viên đã chọn một học sinh làm lớp trưởng và một lớp phó học tập nên lúc này ta có 28 cách chọn một lớp phó văn thể.
Vậy giáo viên có tất cả 30.29.28 = 24360 cách chọn một ban cán sự lớp.
Lời giải:
Vì đội trưởng là người sút lượt thứ nhất và tiền đạo cắm là người sút lượt thứ ba nên chỉ còn 3 lượt sút thứ hai, thứ tư và thứ năm cần sắp xếp.
Sau khi xếp lượt sút của đội trưởng và tiền đạo cắm thì còn 9 cầu thủ để huấn luyện viên lựa chọn.
Việc chọn 3 cầu thủ trong số 9 cầu thủ và xếp thứ tự đá luân lưu của họ là thực hiện 3 hành động liên tiếp: chọn cầu thủ sút lượt thứ hai, sau đó chọn cầu thủ sút lượt thứ tư và cuối cùng là chọn cầu thủ sút lượt thứ năm.
Huấn luyện viên có 9 cách chọn một cầu thủ sút lượt thứ hai.
Vì huấn luyện viên đã chọn một cầu thủ sút lượt thứ hai, nên lúc này ông có 8 cách chọn một cầu thủ sút lượt thứ tư.
Vì huấn luyện viên đã chọn hai cầu thủ sút lượt thứ hai và thứ tư, nên lúc này ông có 7 cách chọn một cầu thủ sút lượt thứ năm.
Vậy huấn luyện viên có tất cả 9.8.7 = 504 cách lập một danh sách 5 cầu thủ đá luân lưu.
a) Hai người đó là một cặp vợ chồng;
b) Hai người đó không là vợ chồng.
Lời giải:
a) Vì có 10 cặp vợ chồng dự tiệc nên ta có 10 nam và 10 nữ.
Việc chọn một cặp vợ chồng để phát biểu ý kiến là thực hiện hai hành động liên tiếp: đầu tiên chọn 1 nam, sau đó chọn 1 nữ là vợ của người nam đã chọn.
Chọn 1 nam có 10 cách chọn.
Chọn 1 nữ là vợ của người nam đã chọn chỉ có 1 cách chọn.
Vậy có tất cả 10.1 = 10 cách chọn hai người trong bữa tiệc để phát biểu ý kiến sao cho hai người đó là một cặp vợ chồng.
b) Việc chọn một cặp vợ chồng để phát biểu ý kiến là thực hiện hai hành động liên tiếp: đầu tiên chọn 1 nam, sau đó chọn 1 nữ không phải là vợ của người nam đã chọn.
Chọn 1 nam có 10 cách chọn.
Chọn 1 nữ không phải là vợ của người nam đã chọn thì có 9 cách chọn.
Vậy có tất cả 10.9 = 90 cách chọn hai người trong bữa tiệc để phát biểu ý kiến sao cho hai người đó không phải là vợ chồng.
a) Vẽ sơ đồ hình cây biểu thị sự hình thành giao tử.
b) Từ đó, tính số loại giao tử của kiểu gen AaBBDdEe.
Lời giải:
a) Sơ đồ hình cây biểu thị sự hình thành giao tử:
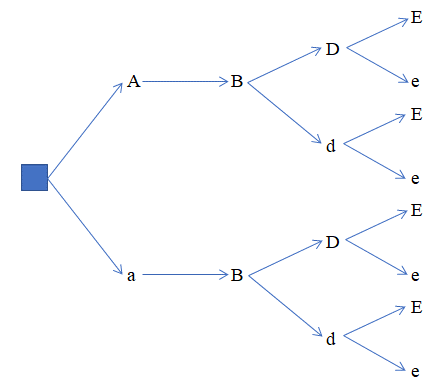
b) Từ sơ đồ cây, ta có 8 loại giao tử của kiểu gen AaBBDdEe là: ABDE, ABDe, ABdE, ABde, aBDE, aBDe, aBdE, aBde.
Xêm thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:
Lý thuyết Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây
I. Quy tắc cộng
Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một) thì công việc đó có m + n cách hoàn thành.
Ví dụ: Một nhóm học sinh ưu tú của lớp 10A có 13 học sinh nam và 7 học sinh nữ. Giáo viên muốn chọn ra 1 bạn để đi dự đại hội dành cho học sinh của khối. Hỏi giáo viên có bao nhiêu cách để chọn học sinh đó.
Hướng dẫn giải
Để chọn 1 học sinh ta thực hiện một trong hai hành động sau:
Chọn một học sinh trong 13 học sinh nam: Có 13 cách chọn.
Chọn một học sinh trong 7 học sinh nữ: Có 7 cách chọn.
Vậy có 13 + 7 = 20 cách chọn 1 học sinh.
Vậy giáo viên có 20 cách để lựa chọn một học sinh để đi dự đại hội.
Nhận xét: Một công việc được hoàn thành bởi một trong ba hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện, hành động thứ ba có p cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một) thì công việc đó có m + n + p cách hoàn thành.
Ví dụ: Nhà trường tổ chức cho học sinh tìm hiểu về các đề tài. Ban tổ chức đưa ra ba nội dung gồm: 5 đề tài về khoa học tự nhiên, 6 đề tài xã hội và 10 đề tài về môi trường và cuộc sống. Hỏi mỗi học sinh có bao nhiêu khả năng lựa chọn. Biết mỗi học sinh chỉ được chọn một đề tài.
Hướng dẫn giải
Mỗi học sinh chọn một đề tài, tức là mỗi học sinh thực hiện một trong ba hành động sau:
Chọn một đề tài trong 5 đề tài về khoa học tự nhiên: Có 5 cách chọn.
Chọn một đề tài trong 6 đề tài về xã hội: Có 6 cách chọn.
Chọn một đề tài trong 10 đề tài về môi trường và cuộc sống: Có 10 cách chọn.
Vậy có 5 + 6 + 10 = 21 cách chọn 1 đề tài.
Vậy mỗi học sinh có 21 khả năng lựa chọn một đề tài để tìm hiểu.
II. Quy tắc nhân
Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện và ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai thì công việc có m.n cách hoàn thành.
Ví dụ: Để đi từ nhà An đến nhà Minh có hai con đường để đi. Từ nhà Minh đến nhà Lâm có ba con đường để đi. Hỏi có bao nhiêu cách lựa chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh.
Hướng dẫn giải
Việc lựa chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh là thực hiện hai hành động liên tiếp.
– Chọn con đường đi từ nhà An đến nhà Minh có 2 cách chọn;
– Chọn con đường đi từ nhà Minh đến nhà Lâm có 3 cách chọn.
Theo quy tắc nhân, ta có 2.3 = 6 cách chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh.
Vậy có 6 cách chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh.
Nhận xét: Một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện và ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai; ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động thứ hai có p cách thực hiện hành động thứ ba thì công việc có m.n.p cách hoàn thành.
Ví dụ: Một người ăn trưa tại một của hàng. Trong thực đơn có 5 món thịt, 3 món rau và 4 món tráng miệng. Hỏi người này có bao nhiêu cách để lựa chọn một bữa ăn gồm 1 món thịt, 1 món rau và 1 món tráng miệng.
Hướng dẫn giải
Để lựa chọn một bữa ăn có 1 món thịt, 1 món rau và 1 món tráng miệng thì phải thực hiện qua ba hành động liên tiếp là:
– Lựa chọn một món thịt: có 5 cách chọn.
– Lựa chọn một món rau: có 3 cách chọn.
– Lựa chọn một món tráng miệng: có 4 cách chọn.
Theo quy tắc nhân, ta có 5.3.4 = 60 cách chọn 1 món thịt, 1 món rau và 1 món tráng miệng.
Vậy người này có 60 cách để lựa chọn một bữa ăn gồm 1 món thịt, 1 món rau và 1 món tráng miệng.
III. Sơ đồ hình cây
Nhận xét:
– Sơ đồ hình cây (Hình 6) là sơ đồ bắt đầu tại một nút duy nhất với cách nhánh tỏa ra các nút bổ sung.
– Ta có thể sử dụng sơ đồ hình cây để đếm số cách hoàn thành một công việc khi công việc đó đòi hỏi những hành động liên tiếp.
Ví dụ: Bạn Diệp muốn mua một chiếc đồng hồ đeo tay. Biết đồng hồ có 3 loại mặt để lựa chọn: mặt vuông, mặt tròn, mặt elip; có 2 loại dây đồng hồ là: dây da màu đen, dây da màu nâu. Hỏi Diệp có bao nhiêu cách để lựa chọn một chiếc đồng hồ.
Hướng dẫn giải
Để lựa chọn một chiếc đồng hồ phải trải qua hai hành động: Lựa chọn mặt đồng đồ, sau đó ứng với mỗi cách lựa chọn mặt đồng hồ ta lại lựa chọn dây đồng hồ.
Khi đó, ta có sơ đồ hình cây mô tả các cách chọn một chiếc đồng hồ như sau:
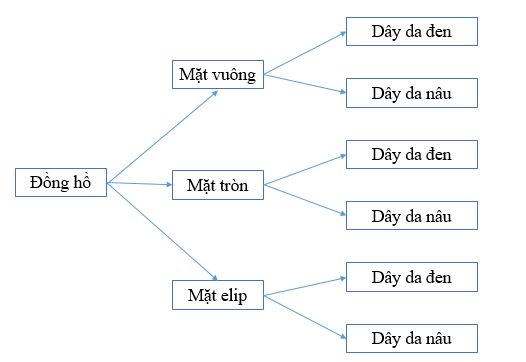
Quan sát sơ đồ hình cây ta thấy có 6 cách lựa chọn một chiếc đồng hồ.
Vậy có 6 cách để bạn Diệp lựa chọn 1 chiếc đồng hồ.
IV. Vận dụng trong bài toán đếm
Việc kiểm đến có ý nghĩa quan trọng trong toán học và thực tiễn, đặc biệt trong thống kê và xác suất. Kết quả đếm cho phép chúng ta xác định số khả năng mà một sự kiện có thể xảy ra để làm cơ sở cho việc đưa ra quyết định. Quy tắc cộng, quy tắc nhân và sơ đồ hình cây là những nguyên tắc cơ bản trong các bài toán đếm.
1. Vận dụng trong giải toán
Ví dụ: Cho 3 chữ số 3; 4; 5. Lập được bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau từ ba chữ số trên.
Hướng dẫn giải
Gọi số có ba chữ số đôi một khác nhau có dạng abc.
Để được một số có ba chữ số ta phải thực hiện 3 hành động liên tiếp.
– Chọn chữ số a: ta chọn một trong 3 chữ số {3; 4; 5}, có 3 cách chọn.
– Chọn chữ số b: chữ số b phải khác chữ số a, nên chữ số b có 2 cách chọn.
– Chọn chữ số c: chữ số c phải khác chữ số a và b nên chữ số c có 1 cách chọn.
Theo quy tắc nhân, ta có 3.2.1 = 6 cách chọn.
Vậy ta lập được 6 số tự nhiên có ba chữ số đôi một khác nhau từ ba chữ số {3; 4; 5}.
2. Vận dụng trong thực tiễn
Ví dụ: Bạn Mai muốn đặt mật khẩu cho điện thoại của mình bằng các chữ số. Biết mật khẩu là dãy số gồm 6 chữ số. Hỏi bạn Mai có bao nhiêu cách để đặt mật khẩu.
Hướng dẫn giải
Gọi mật khẩu cần đặt có dạng abcfeg.
Việc chọn mật khẩu là chọn liên tiếp 6 chữ số a, b, c, d, e, g mỗi chữ số là một trong các chữ số {0; 1; 2; …; 9}.
Chọn a: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.
Chọn b: là chọn 1 trong các chữ số {0;1; 2; …; 9}. Có 10 cách chọn.
Chọn c: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.
Chọn d: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.
Chọn e: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.
Chọn g: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.
Theo quy tắc nhân ta có 10 .10. 10. 10. 10. 10 = 1 000 000 cách đặt mật khẩu.
Vậy Mai có 1 000 000 cách để đặt mật khẩu.