Với giải sách bài tập Toán 10 Bài 6: Tích vô hướng của hai vectơ sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 6: Tích vô hướng của hai vectơ

Giải SBT Toán 10 trang 105 Tập 1

Bài 57 trang 105 SBT Toán 10 Tập 1: Cho tam giác ABC. Giá trị của $\overrightarrow{BA}.\overrightarrow{CA}$ bằng:

A. AB . AC . cos$\widehat{BAC}$.

B. – AB . AC . cos$\widehat{BAC}$.

C. AB . AC . cos$\widehat{ABC}$.

D. AB . AC . cos$\widehat{ACB}$.

Lời giải:

Đáp án đúng là A

Xét tam giác ABC, có:

$$\begin{gathered} \overrightarrow{BA}.\overrightarrow{CA}=\left(-\overrightarrow{AB}\right).\left(-\overrightarrow{AC}\right) \\ =BA.CA.c\text{os}\left(-\overrightarrow{AB},-\overrightarrow{AC}\right) \end{gathered}$$

= $BA.CA.c\text{os}\widehat{BAC}$

= $BA.CA.c\text{os}\left(\widehat{BAC}\right)$

Vậy chọn A.

Bài 58 trang 105 SBT Toán 10 Tập 1: Cho tam giác ABC. Giá trị của $\overrightarrow{AB}.\overrightarrow{BC}$ bằng:

A. AB . BC . cos$\widehat{ABC}$.

B. AB . AC . cos$\widehat{ABC}$.

C. – AB . BC . cos$\widehat{ABC}$.

D. AB . BC . cos$\widehat{BAC}$.

Lời giải:

Đáp án đúng là A

$$\begin{gathered} \overrightarrow{AB}.\overrightarrow{BC}=-\overrightarrow{BA}.\overrightarrow{BC} \\ =-AB.BC.\cos \left(-\overrightarrow{BA},\overrightarrow{BC}\right) \end{gathered}$$

= $-AB.BC.\cos \left(180°-\widehat{ABC}\right)$

= $AB.BC.\cos \widehat{ABC}$.

Vậy chọn A.

Bài 59 trang 105 SBT Toán 10 Tập 1: Cho đoạn thẳng AB. Tập hợp các điểm M nằm trong mặt phẳng thỏa mãn $\overrightarrow{MA}.\overrightarrow{MB}=0$ là:

A. Đường tròn tâm A bán kính AB.

B. Đường tròn tâm B bán kính AB.

C. Đường trung trực của đoạn thẳng AB.

D. Đường tròn đường kính AB.

Lời giải:

Đáp án đúng là D

Ta có: $\overrightarrow{MA}.\overrightarrow{MB}=0$

⇒ $\widehat{\left(\overrightarrow{MA};\overrightarrow{MB}\right)}=\widehat{AMB}=90°$

Do đó tập hợp các điểm M thỏa mãn $\widehat{AMB}=90°$ là đường tròn đường kính AB.

Bài 60 trang 105 SBT Toán 10 Tập 1: Nếu hai điểm M và N thỏa mãn $\overrightarrow{MN}.\overrightarrow{NM}=-9$ thì:

A. MN = 9.

B. MN = 3.

C. MN = 81.

D. MN = 6.

Lời giải:

Đáp án đúng là B

Ta có: 

$$\begin{gathered} \overrightarrow{MN}.\overrightarrow{NM}=MN.MN.cos\left(\overrightarrow{MN},\overrightarrow{NM}\right) \\ =MN.MN.cos180°=-M{N}^2 \end{gathered}$$

Mà $\overrightarrow{MN}.\overrightarrow{NM}=-9$ nên – MN² = – 9 ⇔ MN² = 9 ⇔ MN = 3 (thỏa mãn) hoặc MN = – 3 (không thỏa mãn).

Vậy MN = 3.

Bài 61 trang 105 SBT Toán 10 Tập 1: Cho tam giác ABC đều cạnh a. Các điểm M, N lần lượt thuộc các tia BC và CA thỏa mãn $BM=\frac{1}{3}BC$, $CN=\frac{5}{4}CA$. Tính:

a) $\overrightarrow{AB}.\overrightarrow{AC},\overrightarrow{AM}.\overrightarrow{BN}$.

b) MN.

Lời giải:

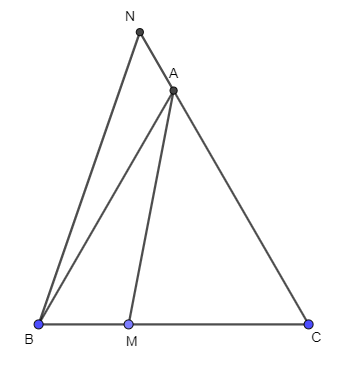
a) Ta có: $\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)$

= $AB.AC.\cos \widehat{BAC}$

= $a.a.\cos 60°$

= $\frac{1}{2}{a}^2$

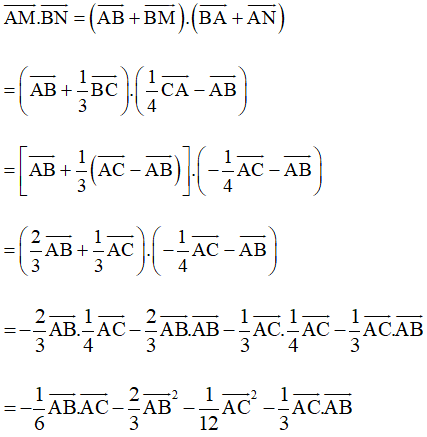
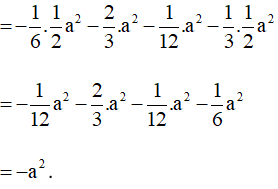
b)  Ta có: 

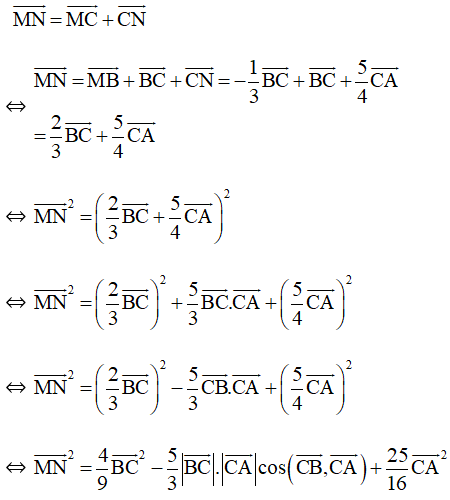
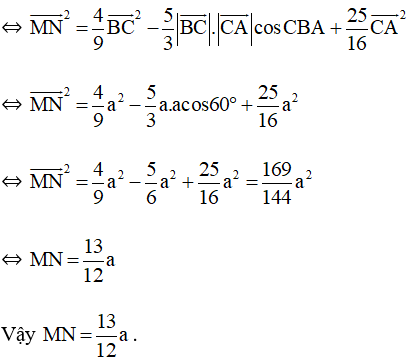
Giải SBT Toán 10 trang 106 Tập 1

Bài 62 trang 106 SBT Toán 10 Tập 1: Cho hình thoi ABCD cạnh a và $\widehat{A}=120°$. Tính $\overrightarrow{AC}.\overrightarrow{BC}$.

Lời giải:

$$\begin{gathered} \overrightarrow{AC}.\overrightarrow{BC}=\left(\overrightarrow{AD}+\overrightarrow{AB}\right).\overrightarrow{AD} \\ ={\overrightarrow{AD}}^2+\overrightarrow{AB}.\overrightarrow{AD} \\ ={\overrightarrow{AD}}^2+AB.AD.c\text{os}\left(\overrightarrow{AB},\overrightarrow{AD}\right) \end{gathered}$$

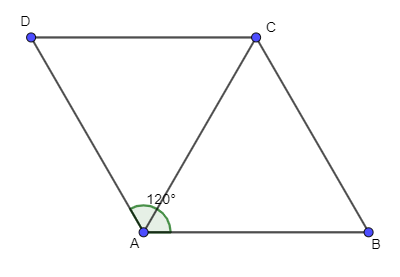
= a² + a.a.cos120°

= a² – $\frac{1}{2}$a² = $\frac{1}{2}$a².

Vậy $\overrightarrow{AC}.\overrightarrow{BC}=\frac{1}{2}{a}^2.$

Bài 63 trang 106 SBT Toán 10 Tập 1: Cho bốn điểm A, B, C, D. Chứng minh $\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0$.

Lời giải:

$\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0$

$=\overrightarrow{AB}.\left(\overrightarrow{AD}-\overrightarrow{AC}\right)+$$\overrightarrow{AC}.\left(\overrightarrow{AB}-\overrightarrow{AD}\right)+\overrightarrow{AD}.\left(\overrightarrow{AC}-\overrightarrow{AB}\right)$

$=\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AC}+\overrightarrow{AC}.\overrightarrow{AB}$$-\overrightarrow{AC}.\overrightarrow{AD}+\overrightarrow{AD}.\overrightarrow{AC}-\overrightarrow{AD}.\overrightarrow{AB}$

$=\left(\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AD}.\overrightarrow{AB}\right)+$$\left(-\overrightarrow{AB}.\overrightarrow{AC}+\overrightarrow{AC}.\overrightarrow{AB}\right)$$+\left(-\overrightarrow{AC}.\overrightarrow{AD}+\overrightarrow{AD}.\overrightarrow{AC}\right)$

= 0

Bài 64* trang 106 SBT Toán 10 Tập 1: Cho hình vuông ABCD, M là trung điểm của BC, N là điểm nằm giữa hai điểm A và C. Đặt x = $\frac{AN}{AC}$. Tìm x thỏa mãn AM ⊥ BN.

Lời giải:

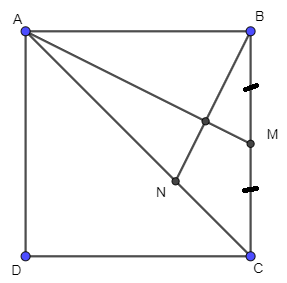
Gọi a là độ dài cạnh của hình vuông ABCD

Vì M là trung điểm của BC nên ta có:

$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}$

⇔ $\overrightarrow{AM}=\overrightarrow{BM}-\overrightarrow{BA}=\frac{1}{2}\overrightarrow{BC}-\overrightarrow{BA}$

Ta lại có:

$$\begin{gathered} \overrightarrow{BN}=\overrightarrow{BA}+\overrightarrow{AN}=-\overrightarrow{AB}+x\overrightarrow{AC} \\ =-\overrightarrow{AB}+x\left(\overrightarrow{AB}+\overrightarrow{BC}\right)=(1-x)\overrightarrow{BA}+x\overrightarrow{BC} \end{gathered}$$

⇒ $\overrightarrow{AM}.\overrightarrow{BN}=\left(\frac{1}{2}\overrightarrow{BC}-\overrightarrow{BA}\right)$$\left[(1-x)\overrightarrow{BA}+x\overrightarrow{BC}\right]$

⇔ $\overrightarrow{AM}.\overrightarrow{BN}=\frac{1}{2}(1-x)\overrightarrow{BC}.\overrightarrow{BA}+$$\frac{1}{2}x{\overrightarrow{BC}}^2-\left(1-x\right){\overrightarrow{BA}}^2-x\overrightarrow{BA}.\overrightarrow{BC}$

⇔ $\overrightarrow{AM}.\overrightarrow{BN}=\frac{1}{2}x.a^2-\left(1-x\right)a^2$

⇔ $\overrightarrow{AM}.\overrightarrow{BN}=\left(\frac{3}{2}x-1\right)a^2$

Để AM vuông góc với BN thì $\overrightarrow{AM}.\overrightarrow{BN}=0$

⇔ $\left(\frac{3}{2}x-1\right)a^2=0$

⇔ $\frac{3}{2}x-1=0$

⇔ $x=\frac{2}{3}$

Vậy với $x=\frac{2}{3}$ thì AM ⊥ BN.

Bài 65 trang 106 SBT Toán 10 Tập 1: Cho tam giác ABC và G là trọng tâm tam giác. Với mỗi điểm M, chứng minh MA² + MB² + MC² = 3MG² + GA² + GB² + GC².

Lời giải:

Ta có: MA² + MB² + MC² = ${\overrightarrow{MA}}^2+{\overrightarrow{MB}}^2+{\overrightarrow{MC}}^2$

= ${\left(\overrightarrow{MG}+\overrightarrow{GA}\right)}^2+{\left(\overrightarrow{MG}+\overrightarrow{GB}\right)}^2+{\left(\overrightarrow{MG}+\overrightarrow{GC}\right)}^2$

= ${\overrightarrow{MG}}^2+2.\overrightarrow{MG}.\overrightarrow{GA}+{\overrightarrow{GA}}^2+{\overrightarrow{MG}}^2$$+2\overrightarrow{MG}.\overrightarrow{GB}+{\overrightarrow{GB}}^2+{\overrightarrow{MG}}^2$$+2\overrightarrow{MG}.\overrightarrow{GC}+{\overrightarrow{GC}}^2$

= $3{\overrightarrow{MG}}^2+\left({\overrightarrow{GA}}^2+{\overrightarrow{GB}}^2+{\overrightarrow{GC}}^2\right)+$$\left(2.\overrightarrow{MG}.\overrightarrow{GA}+2\overrightarrow{MG}.\overrightarrow{GB}+2\overrightarrow{MG}.\overrightarrow{GC}\right)$

= $3M{G}^2+\left(G{A}^2+G{B}^2+G{C}^2\right)$$+2.\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)$

= $3M{G}^2+\left(G{A}^2+G{B}^2+G{C}^2\right)$.

Bài 66 trang 106 SBT Toán 10 Tập 1: Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 650km/h thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ 35km/h. Máy bay bị thay đổi vận tốc đầu khi gặp gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần mười theo đơn vị km/h).

Lời giải:

Gọi $\overrightarrow{v_0}$ là vận tốc của máy bay, $\overrightarrow{v_1}$là vận tốc của gió.

Khi đó ta có: $\left|\overrightarrow{v_0}\right|=650$, $\left|\overrightarrow{v_1}\right|=35$, $\left(\overrightarrow{v_0};\overrightarrow{v_1}\right)=45°$

Tốc độ mới của máy bay là $\overrightarrow{v}=\overrightarrow{v_0}+\overrightarrow{v_1}$ 

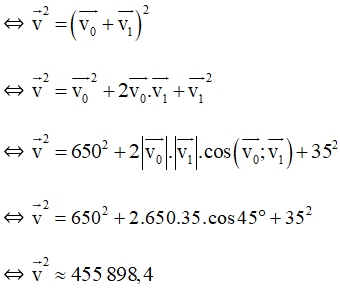
⇔ v = 675,2 km/h.

Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:

Bài 5: Tích của một số với một vectơ

Bài ôn tập chương 4

Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây

Bài 2: Hoán vị. Chỉnh hợp

Lý thuyết Tích vô hướng của hai vectơ

1. Định nghĩa

1.1. Tích vô hướng của hai vectơ có cùng điểm đầu

– Góc giữa hai vectơ $\overrightarrow{\mathrm{OA}}$, $\overrightarrow{\mathrm{OB}}$ là góc giữa hai tia OA, OB và được kí hiệu là $\left(\overrightarrow{\mathrm{OA}},\overrightarrow{\mathrm{OB}}\right)$

– Tích vô hướng của hai vectơ $\overrightarrow{\mathrm{OA}}$ và $\overrightarrow{\mathrm{OB}}$ là một số thực, kí hiệu là $\overrightarrow{\mathrm{OA}}$.$\overrightarrow{\mathrm{OB}}$, được xác định bởi công thức: $\overrightarrow{\mathrm{OA}}.\overrightarrow{\mathrm{OB}}=\left|\overrightarrow{\mathrm{OA}}\right|.\left|\overrightarrow{\mathrm{OB}}\right|.\cos \left(\overrightarrow{\mathrm{OA}},\overrightarrow{\mathrm{OB}}\right)$.

Ví dụ: Cho tam giác ABC đều cạnh 2a có đường cao AH. Tính tích vô hướng của $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AC}}$.

Hướng dẫn giải:

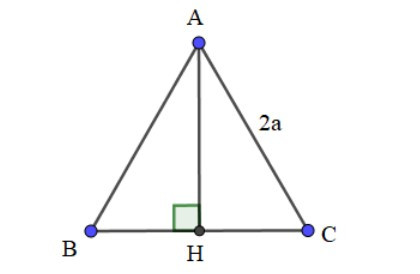
Vì tam giác ABC đều nên $\widehat{\mathrm{BAC}}$ = 60°

⇒ $\left(\overrightarrow{\mathrm{AB}},\overrightarrow{\mathrm{AC}}\right)$ = $\widehat{\mathrm{BAC}}$ = 60°

Ta có:

$\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AC}}$ = $\left|\overrightarrow{\mathrm{AB}}\right|.\left|\overrightarrow{\mathrm{AC}}\right|.\cos \left(\overrightarrow{\mathrm{AB}},\overrightarrow{\mathrm{AC}}\right)$

⇒ $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AC}}$ = AB.AC.cos$\widehat{\mathrm{BAC}}$ = AB.AC.cos60° = 2a.2a.$\frac{1}{2}$ = 2a².

1.2. Tích vô hướng của hai vectơ tùy ý

Định nghĩa:

Cho hai vectơ $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ khác $\overrightarrow{0}.$ Lấy một điểm O và vẽ vectơ $\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{b}}$ (Hình vẽ).

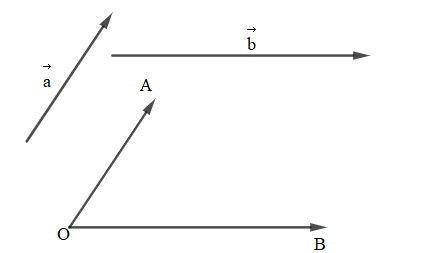
+ Góc giữa hai vectơ $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$, kí hiệu $\left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$, là góc giữa hai vectơ $\overrightarrow{\mathrm{OA}}$, $\overrightarrow{\mathrm{OB}}$.

+ Tích vô hướng của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$, kí hiệu $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{b}}$ là tích vô hướng của hai vectơ $\overrightarrow{\mathrm{OA}}$ và $\overrightarrow{\mathrm{OB}}$. Như vậy, tích vô hướng của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ là một số thực được xác định bởi công thức: $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{b}}$ = $\left|\overrightarrow{\mathrm{a}}\right|.\left|\overrightarrow{\mathrm{b}}\right|.\cos \left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$.

Quy ước: Tích vô hướng của một vectơ bất kì với vectơ $\overrightarrow{0}$ là số 0.

Chú ý:

+) $\left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$ = $\left(\overrightarrow{\mathrm{b}},\overrightarrow{\mathrm{a}}\right)$

+) Nếu $\left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$ = 90° thì ta nói hai vectơ $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ vuông góc với nhau, kí hiệu $\overrightarrow{\mathrm{a}}$ ⊥ $\overrightarrow{\mathrm{b}}$ hoặc $\overrightarrow{\mathrm{b}}$ ⊥ $\overrightarrow{\mathrm{a}}$. Khi đó $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{b}}$ = $\left|\overrightarrow{\mathrm{a}}\right|.\left|\overrightarrow{\mathrm{b}}\right|.\cos 90°$= 0.

+) Tích vô hướng của hai vectơ cùng hướng bằng tích hai độ dài của chúng.

+) Tích vô hướng của hai vectơ ngược hướng bằng số đối của tích hai độ dài của chúng.

Ví dụ: Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AC}}$,$\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{CB}}$.

Hướng dẫn giải:

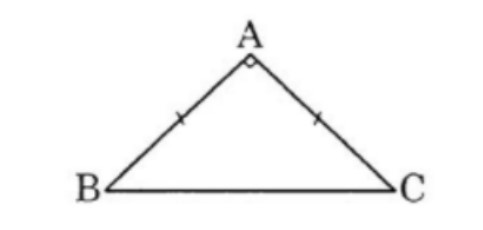
+ Vì tam giác ABC vuông cân, mà AB = AC

⇒ Tam giác ABC vuông cân tại A.

⇒ AB ⊥ AC

⇒ $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AC}}$ = $\left|\overrightarrow{\mathrm{AB}}\right|.\left|\overrightarrow{\mathrm{AC}}\right|.\cos 90°$ = $\left|\overrightarrow{\mathrm{AB}}\right|.\left|\overrightarrow{\mathrm{AC}}\right|.0$ = 0

+ Ta có: BC = $\sqrt{{\mathrm{AB}}^2+{\mathrm{AC}}^2}$ = $\sqrt{{\mathrm{a}}^2+{\mathrm{a}}^2}$ = a$\sqrt{2}$.

⇒ $\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{CB}}$ = $\left|\overrightarrow{\mathrm{AC}}\right|.\left|\overrightarrow{\mathrm{CB}}\right|.\cos \left(\overrightarrow{\mathrm{AC}},\overrightarrow{\mathrm{CB}}\right)$ = a. a$\sqrt{2}$.cos135° = a. a$\sqrt{2}$.$\left(\frac{-\sqrt{2}}{2}\right)$ = –a².

2. Tính chất

Với hai vectơ bất kì $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ và số thực k tùy ý, ta có:

+) $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{b}}$ = $\overrightarrow{\mathrm{b}}$.$\overrightarrow{\mathrm{a}}$ (tính chất giao hoán);

+) $\overrightarrow{\mathrm{a}}.\left(\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}}\right)=\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{c}}$ (tính chất phân phối);

+) $\left(\mathrm{k}\overrightarrow{\mathrm{a}}\right)\overrightarrow{\mathrm{b}}=\mathrm{k}\left(\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}\right)=\overrightarrow{\mathrm{a}}.\left(\mathrm{k}\overrightarrow{\mathrm{b}}\right)$;

+) ${\overrightarrow{\mathrm{a}}}^2$ ≥ 0, ${\overrightarrow{\mathrm{a}}}^2$ = 0 ⟺ $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$.

Trong đó, kí hiệu $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{a}}$ = ${\overrightarrow{\mathrm{a}}}^2$ và biểu thức này được gọi là bình phương vô hướng của vectơ $\overrightarrow{\mathrm{a}}$.

Ví dụ: Cho 4 điểm A, B, C, D bất kì. Chứng minh: $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{BC}}.\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{BD}}=0$.

Hướng dẫn giải:

Ta có:

$\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{CD}}$ = $\overrightarrow{\mathrm{AB}}.\left(\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{AD}}\right)$ = $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AD}}$ (tính chất phân phối)

$\overrightarrow{\mathrm{BC}}.\overrightarrow{\mathrm{AD}}$ = $\left(\overrightarrow{\mathrm{BA}}+\overrightarrow{\mathrm{AC}}\right).\overrightarrow{\mathrm{AD}}$ = $\overrightarrow{\mathrm{BA}}.\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{AD}}$ = $-\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{AD}}$ (tính chất phân phối)

$\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{BD}}$  = $\overrightarrow{\mathrm{CA}}.\left(\overrightarrow{\mathrm{BA}}+\overrightarrow{\mathrm{AD}}\right)$ = $\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{BA}}+\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{AD}}$ = $-\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{AD}}$ (tính chất phân phối)

$\Rightarrow \overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{BC}}.\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{BD}}$

$=\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AD}}-\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{AD}}-\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{AD}}$

= $\left(\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{CA}}-\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{AB}}\right)+\left(\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AD}}-\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AD}}\right)+\left(\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{AD}}-\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{AD}}\right)$ (tính chất giao hoán và kết hợp)

= 0

⟺ $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{BC}}.\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{BD}}=0$ (đpcm).

3. Một số ứng dụng

3.1. Tính độ dài của đoạn thẳng

Nhận xét:

Với hai điểm A, B phân biệt, ta có: ${\overrightarrow{\mathrm{AB}}}^2={\left|\overrightarrow{\mathrm{AB}}\right|}^2$.

Do đó độ dài đoạn thẳng AB được tính như sau: AB = $\sqrt{{\overrightarrow{\mathrm{AB}}}^2}$

3.2. Chứng minh hai đường thẳng vuông góc

Nhận xét:

+ Cho hai vectơ bất kì $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ khác vectơ $\overrightarrow{0}$. Ta có: $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{b}}$ = 0  ⟺ $\overrightarrow{\mathrm{a}}$ ⊥ $\overrightarrow{\mathrm{b}}$.

Hai đường thẳng AB và CD vuông góc với nhau khi và chỉ khi $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{CD}}=0.$+ Hai đường thẳng a và b vuông góc khi và chỉ khi $\overrightarrow{\mathrm{u}}.\overrightarrow{\mathrm{v}}=0$, trong đó $\overrightarrow{\mathrm{u}}$ ≠ 0, $\overrightarrow{\mathrm{v}}$ ≠ 0, giá của vectơ $\overrightarrow{\mathrm{u}}$ song song hoặc trùng với đường thẳng a và giá của vectơ $\overrightarrow{\mathrm{v}}$ song song hoặc trùng với đường thẳng b.

Ví dụ: Cho hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ vuông góc với nhau và $\left|\overrightarrow{\mathrm{a}}\right|=1$, $\left|\overrightarrow{\mathrm{b}}\right|=\sqrt{2}$. Chứng minh hai vectơ 2$\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$ và $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ vuông góc với nhau.

Hướng dẫn giải:

Vì $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ vuông góc với nhau ⟺ $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{b}}$ = 0

Ta có:

$\left(2 \overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}}\right)\left(\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}\right)$ = $2{\overrightarrow{\mathrm{a}}}^2+2\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}-\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}-{\overrightarrow{\mathrm{b}}}^2$ = $2{\overrightarrow{\mathrm{a}}}^2+\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}-{\overrightarrow{\mathrm{b}}}^2$ = $2{\left|\overrightarrow{\mathrm{a}}\right|}^2+\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}-{\left|\overrightarrow{\mathrm{b}}\right|}^2$

= 2.1² + 0 – ${\left(\sqrt{2}\right)}^2$ = 0

Vì tích của hai vectơ 2$\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$ và $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ bằng 0 nên chúng vuông góc với nhau.