Với lời giải SBT Toán 10 trang 102 Tập 1 chi tiết trong Bài tập cuối chương 5 sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài tập cuối chương 5

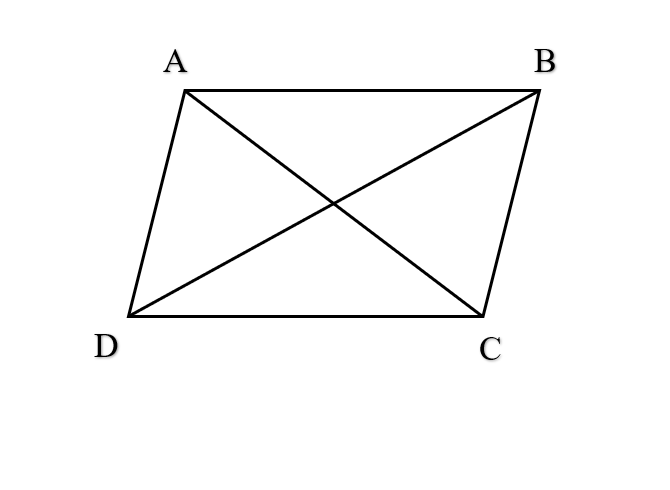
Bài 6 trang 102 SBT Toán 10 Tập 1: Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng?

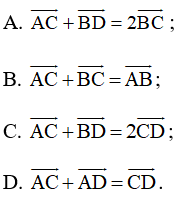
Lời giải:

Đáp án đúng là A

Ta có:

( vì ). Vậy khẳng định A đúng. Khẳng định C sai.

Ta có: . Do đó khẳng định B sai.

Ta lại có: . Do đó khẳng định D sai.

Vậy chọn đáp án A.

Bài 7 trang 102 SBT Toán 10 Tập 1: Cho tam giác ABC. Đặt $\overrightarrow{\text{a}}=\overrightarrow{\text{BC}}$, $\overrightarrow{\text{b}}=\overrightarrow{\text{AC}}\text{}$. Các cặp vectơ nào sau đây cùng phương?

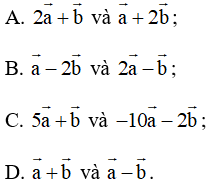
Lời giải:

Đáp án đúng là C

Ta có thể thấy:

Như vậy  và  là cặp vectơ cùng phương.

Bài 8 trang 102 SBT Toán 10 Tập 1: Cho tam giác ABC vuông ở A và có $\widehat{\text{B}}$ = 50°. Khẳng định nào sau đây là sai?

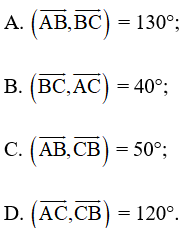
Lời giải:

Đáp án đúng là D

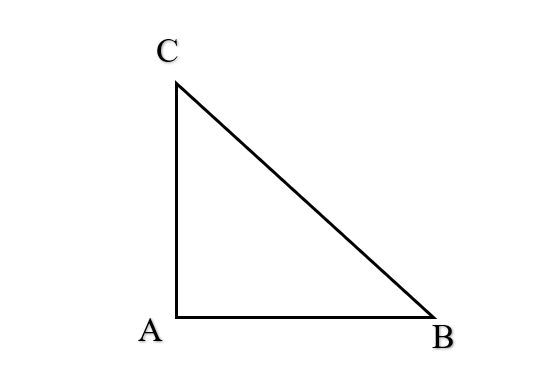
Ta có: $\left(\overrightarrow{\text{AB}},\overrightarrow{\text{BC}}\right)=\left(-\overrightarrow{\text{BA}},\overrightarrow{\text{BC}}\right)=-\left(\overrightarrow{\text{BA}},\overrightarrow{\text{BC}}\right)$ là góc kề bù với $\widehat{\text{ABC}}$ 

⇒ $\left(\overrightarrow{\text{AB}},\overrightarrow{\text{BC}}\right)$ = 180° – 50° = 130°. Khẳng định A đúng.

$\left(\overrightarrow{\text{BC}},\overrightarrow{\text{AC}}\right)$ = $\left(\overrightarrow{\text{CB}},\overrightarrow{\text{CA}}\right)$ = $\widehat{\text{ACB}}$ = 90° – 50° = 40°. Khẳng định B đúng.

$\left(\overrightarrow{\text{AB}},\overrightarrow{\text{CB}}\right)$ = $\left(\overrightarrow{\text{BA}},\overrightarrow{\text{BC}}\right)$ = $\widehat{\text{ABC}}$ = 50°. Khẳng định C đúng.

$\left(\overrightarrow{\text{AC}},\overrightarrow{\text{CB}}\right)=\left(-\overrightarrow{\text{CA}},\overrightarrow{\text{CB}}\right)=-\left(\overrightarrow{\text{CA}},\overrightarrow{\text{CB}}\right)$ là góc kề bù với $\widehat{\text{ACB}}$ 

⇒ $\left(\overrightarrow{\text{AC}},\overrightarrow{\text{CB}}\right)$ = 180° – 40° = 140°. Khẳng định D sai.

Vậy chọn đáp án D.

Bài 9 trang 102 SBT Toán 10 Tập 1: Cho $\overrightarrow{\text{a}}$ và $\overrightarrow{\text{b}}$ là hai vectơ cùng hướng và đều khác vectơ $\overrightarrow{0}$. Khẳng định nào sau đây là đúng?

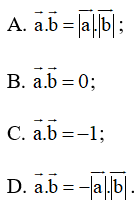
Lời giải:

Đáp án đúng là A

Ta có:

Do $\overrightarrow{\text{a}}$ và $\overrightarrow{\text{b}}$ là hai vectơ cùng hướng và đều khác vectơ $\overrightarrow{\text{0}}$ nên  = cos0° = 1.

Vậy . Đáp án A đúng.

Bài 10 trang 102 SBT Toán 10 Tập 1: Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là sai?

Lời giải:

Đáp án đúng là D

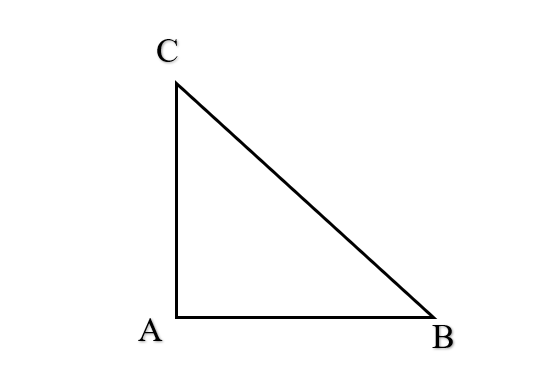
Do AB ⊥ AC nên 

Ta lại có  (vì $\widehat{B}$ là góc nhọn nên cos$\widehat{B}$ > 0). Do đó $\overrightarrow{\text{AB}}.\overrightarrow{\text{AC}}<\overrightarrow{\text{BA}}.\overrightarrow{\text{BC}}\text{}$.

Khẳng định A đúng.

$\left(\overrightarrow{\text{AC}},\overrightarrow{\text{CB}}\right)=\left(-\overrightarrow{\text{CA}},\overrightarrow{\text{CB}}\right)=-\left(\overrightarrow{\text{CA}},\overrightarrow{\text{CB}}\right)$ là góc tù nên $\overrightarrow{\text{AC}}.\overrightarrow{\text{CB}}=\overrightarrow{\left|\text{AC}\right|}.\left|\overrightarrow{\text{CB}}\right|.\cos \left(\overrightarrow{\text{AC}}.\overrightarrow{\text{CB}}\right)$ < 0;

$\left(\overrightarrow{\text{AC}}.\overrightarrow{\text{BC}}\right)$ là góc nhọn nên $\overrightarrow{\text{AC}}.\overrightarrow{\text{BC}}=\left|\overrightarrow{\text{AC}}\right|.\overrightarrow{\left|\text{BC}\right|}.\cos \left(\overrightarrow{\text{AC}}.\overrightarrow{\text{BC}}\right)$> 0. Suy ra $\overrightarrow{\text{AC}}.\overrightarrow{\text{CB}}<\overrightarrow{\text{AC}}.\overrightarrow{\text{BC}}\text{}$. Khẳng định B đúng.

$\left(\overrightarrow{\text{AB}},\overrightarrow{\text{BC}}\right)=\left(-\overrightarrow{BA},\overrightarrow{\text{BC}}\right)=-\left(\overrightarrow{BA},\overrightarrow{\text{BC}}\right)$ là góc tù nên $\overrightarrow{\text{AB}}.\overrightarrow{\text{BC}}$ < 0; $\left(\overrightarrow{\text{CA}}.\overrightarrow{\text{CB}}\right)$ là góc nhọn nên $\overrightarrow{\text{CA}}.\overrightarrow{\text{CB}}$ > 0. Suy ra $\overrightarrow{\text{AB}}.\overrightarrow{\text{BC}}<\overrightarrow{\text{CA}}.\overrightarrow{\text{CB}}$. Khẳng định C đúng.

$\left(\overrightarrow{\text{AC}}.\overrightarrow{\text{BC}}\right)$ là góc nhọn nên $\overrightarrow{\text{AC}}.\overrightarrow{\text{BC}}$ > 0; $\left(\overrightarrow{\text{BC}}.\overrightarrow{\text{AB}}\right)$ là góc tù nên $\overrightarrow{\text{BC}}.\overrightarrow{\text{AB}}$ < 0. Suy ra $\overrightarrow{\text{AC}}.\overrightarrow{\text{BC}}>\overrightarrow{\text{BC}}.\overrightarrow{\text{AB}}$.

Khẳng định D sai.

Vậy chọn đáp án D.

B. Tự luận

Bài 1 trang 102 SBT Toán 10 Tập 1: Cho ba điểm A, B, C phân biệt thẳng hàng. Trong trường hợp nào thì hai vectơ $\overrightarrow{\text{AB}}$ và $\overrightarrow{\text{AC}}$:

a) cùng hướng?

b) ngược hướng?

Lời giải:

a) Hai vectơ $\overrightarrow{\text{AB}}$ và $\overrightarrow{\text{AC}}$ cùng hướng khi B nằm giữa A và C.

b) Hai vectơ $\overrightarrow{\text{AB}}$ và $\overrightarrow{\text{AC}}$ ngược hướng khi A nằm giữa B và C.

Bài 2 trang 102 SBT Toán 10 Tập 1: Cho ba vectơ  cùng phương. Chứng tỏ rằng có ít nhất hai vectơ cùng hướng trong ba vectơ đó.

Lời giải:

Trong ba vectơ  chọn hai vectơ tùy ý:

- Nếu chúng cùng hướng thì đó là hai vectơ cần tìm.

- Nếu chúng ngược hướng thì vectơ còn lại sẽ cùng hướng với một trong hai vectơ đã chọn.

Bài 3 trang 102 SBT Toán 10 Tập 1: Cho tam giác ABC nội tiếp trong đường tròn (O). Gọi H là trực tâm tam giác ABC và B’ là điểm đối xứng với B qua tâm O. Hãy so sánh các vectơ $\overrightarrow{\text{AH}}$ và $\overrightarrow{\text{B'C}}$, $\overrightarrow{\text{AB'}}$ và $\overrightarrow{\text{HC}}$.

Lời giải:

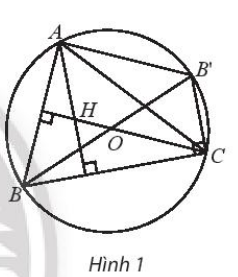
Do BB’ là đường kính nên $\widehat{\text{BCB'}}$ = 90° ( góc nội tiếp chắn nửa đường tròn )

⇒ BC ⊥ B’C.

H là trực tâm tam giác ABC nên BC ⊥ AH.

Suy ra AH // B’C ( do đều vuông góc với BC ).

Do BB’ là đường kính nên $\widehat{\text{BAB'}}$= 90° ( góc nội tiếp chắn nửa đường tròn )

⇒ BA ⊥ B’A.

H là trực tâm tam giác ABC nên CH ⊥ BA.

Suy ra CH // B’A ( do đều vuông góc với BA ).

Như vậy AB’CH là hình bình hành ( DHNB hình bình hành )

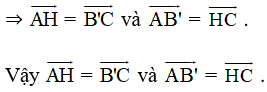
Xem thêm các bài giải sách bài tập Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 101 Tập 1

Giải SBT Toán 10 trang 103 Tập 1

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Tích vô hướng của hai vectơ

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu