Với giải sách bài tập Toán 10 Bài 4: Tích vô hướng của hai vectơ sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 4: Tích vô hướng của hai vectơ

Giải SBT Toán 10 trang 100 Tập 1

Bài 1 trang 100 SBT Toán 10 Tập 1: Cho tam giác vuông cân ABC có AB = AC = a.

Tính các tích vô hướng $\overrightarrow{\mathrm{AB}}.\overrightarrow{\text{AC}}$, $\overrightarrow{\mathrm{AC}}.\overrightarrow{\text{CB}}$.

Lời giải:

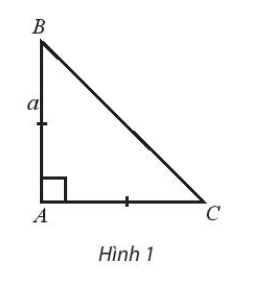
Do tam giác ABC vuông tại A nên AB ⊥ AC ⇒ $\overrightarrow{\mathrm{AB}}.\overrightarrow{\text{AC}}$ = 0;

Ta có: 

Tam giác ABC vuông cân tại A nên $\widehat{\text{ACB}}$ = 45°

Như vậy: 

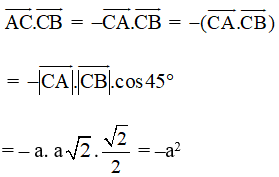
Vậy $\overrightarrow{\mathrm{AB}}.\overrightarrow{\text{AC}}$ = 0 và $\overrightarrow{\text{AC}}.\overrightarrow{\text{CB}}$= –a².

Bài 2 trang 100 SBT Toán 10 Tập 1: Cho hình chữ nhật ABCD có tâm O và AD = 2a, AB = a. Tính:

a) $\overrightarrow{\text{AB}}.\overrightarrow{\text{AO}}$;

b) $\overrightarrow{\text{AB}}.\overrightarrow{\text{AD}}$.

Lời giải:

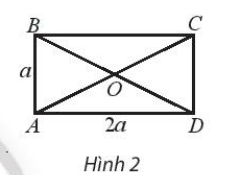
a) Vì ABCD là hình chữ nhật nên AB = CD = a, AD = BC = 2a.

Ta có: AC = $\sqrt{{\text{AB}}^2+{\text{BC}}^2}$ = $\sqrt{{\text{a}}^2+{\left(2\text{a}\right)}^2}$ = a$\sqrt{5}$.

Xét tam giác BAC vuông tại B, có: cos$\widehat{\mathrm{BAO}}$ = cos$\widehat{\mathrm{BAC}}$= $\frac{\text{AB}}{\text{AC}}=\frac{a}{\sqrt{5}a}=\frac{1}{\sqrt{5}}$.

ABCD là hình chữ nhật nên O là trung điểm của AC và BD

⇒ AO = $\frac{1}{2}$AC = $\frac{\text{a}\sqrt{5}}{2}$.

$\overrightarrow{\text{AB}}.\overrightarrow{\text{AO}}$ = $\left|\overrightarrow{\text{AB}}\right|.\left|\overrightarrow{\text{AO}}\right|$. cos$\widehat{\mathrm{BAO}}$ =

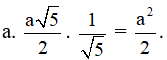
Vậy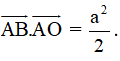 

b) Do ABCD là hình chữ nhật nên 

Giải SBT Toán 10 trang 101 Tập 1

Bài 3 trang 101 SBT Toán 10 Tập 1: Cho nửa đường tròn tâm O có đường kính AB = 2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho AM và BN cắt nhau tại I như Hình 5.

a) Chứng minh 

b) Tính  theo R.

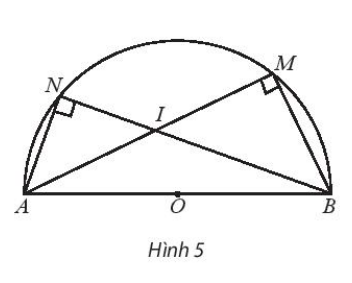
Lời giải:

a) AB là đường kính nên $\widehat{\text{AMB}}$ = $\widehat{\text{ANB}}$ = 90° ( góc nội tiếp chắn nửa đường tròn ).

AM ⊥ MB và AN ⊥ NB.

Ta có:

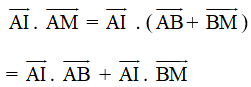
Mà AI ⊥ BM do AM ⊥ MB nên 

Như vậy 

Tương tự ta có: 

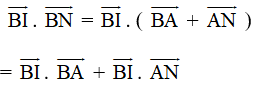
Mà BI ⊥ AN do AN ⊥ NB nên 

Như vậy 

b) Ta có:

Bài 4 trang 101 SBT Toán 10 Tập 1: Tính công sinh bởi một lực $\overrightarrow{\text{F}}$ có độ lớn 60N kéo một vật dịch chuyển một vectơ $\overrightarrow{\text{d}}$ có độ dài 200 m. Biết $\left(\overrightarrow{\text{F}}\text{, }\overrightarrow{\text{d}}\right)$ = 60°.

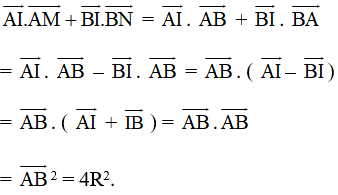
Lời giải:

Áp dụng công thức tính công ta có:

= 60.200.cos60° = 6000 (J).

Vậy công sinh bởi lực $\overrightarrow{F}$ bằng 6000 J.

Bài 5 trang 101 SBT Toán 10 Tập 1: Cho hai vectơ có độ dài lần lượt là 6 và 8 có tích vô hướng là 24. Tính góc giữa hai vectơ đó.

Lời giải:

Gọi hai vectơ lần lượt là $\overrightarrow{{\text{v}}_{\text{1}}}$, $\overrightarrow{{\text{v}}_{\text{2}}}$ và góc giữa hai vectơ là α.

Ta có  = 6.8.cos α = 24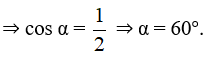 

Vậy góc giữa hai vectơ đề cho là 60°.

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Tích của một số với một vectơ

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

Lý thuyết Tích vô hướng của hai vectơ

1. Góc giữa hai vectơ

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác $\overrightarrow{0}$. Từ một điểm O bất kì ta vẽ $\overrightarrow{OA}=\overrightarrow{a}$, $\overrightarrow{OB}=\overrightarrow{b}$.

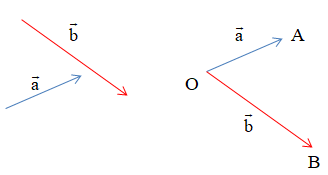
Góc $\widehat{AOB}$ với số đo từ 0° đến 180° được gọi là góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$.

Ta kí hiệu góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ là $\left(\overrightarrow{a},\overrightarrow{b}\right)$.

Nếu $\left(\overrightarrow{a},\overrightarrow{b}\right)=90°$ thì ta nói rằng $\overrightarrow{a}$ và $\overrightarrow{b}$ vuông góc với nhau, kí hiệu $\overrightarrow{a}\perp \overrightarrow{b}$.

Chú ý:

+ Từ định nghĩa, ta có $\left(\overrightarrow{a},\overrightarrow{b}\right)=\left(\overrightarrow{b},\overrightarrow{a}\right)$.

+ Góc giữa hai vectơ cùng hướng và khác $\overrightarrow{0}$ luôn bằng 0°.

+ Góc giữa hai vectơ ngược hướng và khác $\overrightarrow{0}$ luôn bằng 180°.

+ Trong trường hợp có ít nhất một trong hai vectơ $\overrightarrow{a}$ hoặc $\overrightarrow{b}$ là $\overrightarrow{0}$ thì ta quy ước số đo góc giữa hai vectơ đó là tùy ý (từ 0° đến 180°).

Ví dụ: Cho hình thoi ABCD có O là giao điểm của hai đường chéo và $\widehat{BAD}=60°$. Tính số đo các góc:

a) $\left(\overrightarrow{OD},\overrightarrow{CD}\right)$.

b) $\left(\overrightarrow{OB},\overrightarrow{AO}\right)$.

c) $\left(\overrightarrow{OC},\overrightarrow{AC}\right)$.

d) $\left(\overrightarrow{OA},\overrightarrow{AC}\right)$.

Hướng dẫn giải

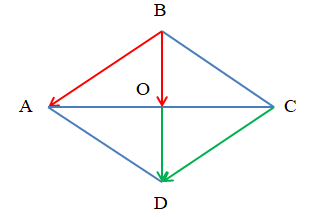
a) Vì O là giao điểm của hai đường chéo nên O là trung điểm BD (tính chất hình thoi).

Suy ra OD = BO.

Mà $\overrightarrow{OD},\overrightarrow{BO}$ cùng hướng.

Do đó $\overrightarrow{OD}=\overrightarrow{BO}$  (1).

Vì ABCD là hình thoi nên ta có CD // BA và CD = BA.

Mà $\overrightarrow{CD},\overrightarrow{BA}$ cùng hướng.

Do đó $\overrightarrow{CD}=\overrightarrow{BA}$  (2).

Từ (1) (2), ta suy ra $\left(\overrightarrow{OD},\overrightarrow{CD}\right)=\left(\overrightarrow{BO},\overrightarrow{BA}\right)=\widehat{OBA}$.

Vì ABCD là hình thoi nên AB = AD.

Do đó tam giác ABD cân tại A.

Mà $\widehat{BAD}=60°$.

Suy ra tam giác ABD đều.

Do đó $\widehat{DBA}=60°$ hay $\widehat{OBA}=60°$.

Vậy $\left(\overrightarrow{OD},\overrightarrow{CD}\right)=\widehat{OBA}=60°$.

b) Vì O là giao điểm của hai đường chéo nên O là trung điểm AC (tính chất hình thoi).

Do đó AO = OC.

Mà $\overrightarrow{AO},\overrightarrow{OC}$ cùng hướng.

Do đó $\overrightarrow{AO}=\overrightarrow{OC}$.

Ta suy ra $\left(\overrightarrow{OB},\overrightarrow{AO}\right)=\left(\overrightarrow{OB},\overrightarrow{OC}\right)=\widehat{BOC}$.

Vì ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau.

Do đó $\widehat{BOC}=90°$.

Vậy $\left(\overrightarrow{OB},\overrightarrow{AO}\right)=\widehat{BOC}=90°$.

c) Vì $\overrightarrow{OC},\overrightarrow{AC}$ cùng hướng nên $\left(\overrightarrow{OC},\overrightarrow{AC}\right)=0°$.

d) Vì $\overrightarrow{OA},\overrightarrow{AC}$ ngược hướng nên $\left(\overrightarrow{OA},\overrightarrow{AC}\right)=180°$.

2. Tích vô hướng của hai vectơ

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác $\overrightarrow{0}$.

Tích vô hướng của $\overrightarrow{a}$ và $\overrightarrow{b}$ là một số, kí hiệu là $\overrightarrow{a}.\overrightarrow{b}$, được xác định bởi công thức:$\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos \left(\overrightarrow{a},\overrightarrow{b}\right)$.

Chú ý:

a) Trường hợp có ít nhất một trong hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bằng $\overrightarrow{0}$, ta quy ước $\overrightarrow{a}.\overrightarrow{b}=0$.

b) Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, ta có $\overrightarrow{a}\perp \overrightarrow{b}\iff \overrightarrow{a}.\overrightarrow{b}=0$.

c) Khi $\overrightarrow{a}=\overrightarrow{b}$ thì tích vô hướng $\overrightarrow{a}.\overrightarrow{b}$ được kí hiệu là ${\overrightarrow{a}}^2$ và được gọi là bình phương vô hướng của vectơ $\overrightarrow{a}$.

Ta có ${\overrightarrow{a}}^2=\left|\overrightarrow{a}\right|.\left|\overrightarrow{a}\right|.\cos 0°={\left|\overrightarrow{a}\right|}^2$. Vậy bình phương vô hướng của một vectơ luôn bằng bình phương độ dài của vectơ đó.

Ví dụ: Cho tam giác ABC vuông cân tại A, có AB = AC = a. Tính các tích vô hướng: $\overrightarrow{AB}.\overrightarrow{AC},\overrightarrow{AC}.\overrightarrow{BC},\overrightarrow{BA}.\overrightarrow{BC}$.

Hướng dẫn giải

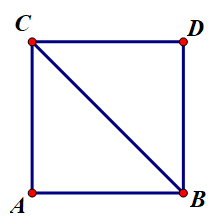
- Tam giác ABC vuông cân tại A nên AB ⊥ AC.

Do đó $\overrightarrow{AB}\perp \overrightarrow{AC}$.

Vậy $\overrightarrow{AB}.\overrightarrow{AC}=0$.

- Vẽ $\overrightarrow{BD}=\overrightarrow{AC}$. Khi đó ta có $\left(\overrightarrow{AC},\overrightarrow{BC}\right)=\left(\overrightarrow{BD},\overrightarrow{BC}\right)=\widehat{CBD}$.

Vì $\overrightarrow{BD}=\overrightarrow{AC}$ nên ta có ABDC là hình bình hành.

Mà $\widehat{BAC}=90°$ và AB = AC (tam giác ABC vuông cân tại A).

Do đó ABDC là hình vuông.

Ta suy ra đường chéo BC là phân giác của $\widehat{ABD}$.

Do đó $\widehat{CBD}=\frac{\widehat{ABD}}{2}=\frac{90°}{2}=45°$.

Khi đó ta có $\left(\overrightarrow{AC},\overrightarrow{BC}\right)=\widehat{CBD}=45°$.

Tam giác ABC vuông cân tại A: BC² = AB² + AC² (Định lý Py ‒ ta ‒ go)

⇔ BC² = a² + a² = 2a²

⇒ BC = $a\sqrt{2}$.

Ta có: $\overrightarrow{AC}.\overrightarrow{BC}=\left|\overrightarrow{AC}.\right|.\left|\overrightarrow{BC}\right|.\cos \left(\overrightarrow{AC},\overrightarrow{BC}\right)=AC.BC.\cos 45°=a.a\sqrt{2}.\frac{\sqrt{2}}{2}=a^2$.

- Tam giác ABC cân tại A. Ta suy ra $\widehat{ACB}=\widehat{ABC}$.

Tam giác ABC vuông tại A: $\widehat{ACB}+\widehat{ABC}=90°$ .

$\iff 2\widehat{ABC}=90°$.

Do đó $\widehat{ABC}=45°$.

Suy ra $\left(\overrightarrow{BA},\overrightarrow{BC}\right)=\widehat{ABC}=45°$.

Ta có $\overrightarrow{BA}.\overrightarrow{BC}=\left|\overrightarrow{BA}\right|.\left|\overrightarrow{BC}\right|.\cos \left(\overrightarrow{BA},\overrightarrow{BC}\right)=BA.BC.\cos 45°=a.a\sqrt{2}.\frac{\sqrt{2}}{2}=a^2$.

Chú ý: Trong Vật lí, tích vô hướng của $\overrightarrow{F}$ và $\overrightarrow{d}$ biểu diễn công A sinh bởi lực $\overrightarrow{F}$ khi thực hiện độ dịch chuyển $\overrightarrow{d}$. Ta có công thức: $A=\overrightarrow{F}.\overrightarrow{d}$.

Ví dụ: Một người dùng một lực $\overrightarrow{F}$ có độ lớn là 150 N kéo một thùng gỗ trượt trên sàn nhà bằng một sợi dây có phương hợp góc 45° so với phương ngang. Tính công sinh bởi lực $\overrightarrow{F}$ khi thùng gỗ trượt được 40 m.

Hướng dẫn giải

Gọi A, $\overrightarrow{d}$ lần lượt là công sinh bởi lực $\overrightarrow{F}$ và độ dịch chuyển của thùng gỗ.

Theo đề, ta có lực $\overrightarrow{F}$ hợp với phương ngang (hướng dịch chuyển) một góc 45°.

Suy ra $\left(\overrightarrow{F},\overrightarrow{d}\right)=45°$.

Ta có A = $\overrightarrow{F}.\overrightarrow{d}=\left|\overrightarrow{F}\right|.\left|\overrightarrow{d}\right|.\cos \left(\overrightarrow{F},\overrightarrow{d}\right)=\mathrm{150.40.}\cos 45°=3000\sqrt{2}$ (J).

Vậy công sinh bởi lực $\overrightarrow{F}$ là $3000\sqrt{2}$ (J).

3. Tính chất của tích vô hướng

Với ba vectơ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ bất kì và mọi số k, ta có:

$\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}$;                       $\overrightarrow{a}.\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}$;                         $\left(k\overrightarrow{a}\right).\overrightarrow{b}=k\left(\overrightarrow{a}.\overrightarrow{b}\right)=\overrightarrow{a}.\left(k\overrightarrow{b}\right)$.

Ví dụ: Áp dụng các tính chất của tích vô hướng, chứng minh rằng:

${\left(\overrightarrow{a}-\overrightarrow{b}\right)}^2={\overrightarrow{a}}^2-2\overrightarrow{a}.\overrightarrow{b}+{\overrightarrow{b}}^2$.

Hướng dẫn giải

Ta có: ${\left(\overrightarrow{a}-\overrightarrow{b}\right)}^2=\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)=\overrightarrow{a}.\overrightarrow{a}-\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}.\overrightarrow{b}={\overrightarrow{a}}^2-2\overrightarrow{a}.\overrightarrow{b}+{\overrightarrow{b}}^2$.

Vậy ta có điều phải chứng minh.

Nhận xét: Chứng minh tương tự, ta cũng có:

${\left(\overrightarrow{a}+\overrightarrow{b}\right)}^2={\overrightarrow{a}}^2+2\overrightarrow{a}.\overrightarrow{b}+{\overrightarrow{b}}^2$;

$\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)={\overrightarrow{a}}^2-{\overrightarrow{b}}^2$.

Ví dụ: Cho tam giác ABC có a = BC, b = AC, c = AB. Tính cạnh BC theo hai cạnh còn lại và góc A bằng cách sử dụng tính chất của vectơ và tích vô hướng của hai vectơ.

Hướng dẫn giải

Ta có BC² = ${\overrightarrow{BC}}^2={\left(\overrightarrow{AC}-\overrightarrow{AB}\right)}^2={\overrightarrow{AC}}^2+{\overrightarrow{AB}}^2-2.\overrightarrow{AC}.\overrightarrow{AB}$

                 $=A{C}^2+A{B}^2-2.\left|\overrightarrow{AC}\right|.\left|\overrightarrow{AB}\right|.\cos \left(\overrightarrow{AC},\overrightarrow{AB}\right)$

                 = AC² + AB² – 2AC.AB.cosA

Vậy BC² = AC² + AB² – 2AC.AB.cosA hay a² = b² + c² – 2bc.cosA.