Giải SGK Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 5

Nguyễn Linh Anh Ngày: 24-08-2024 Lớp 10

5 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài tập cuối chương 5 chi tiết sách Toán 10 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài tập cuối chương 5

Giải toán lớp 10 trang 102 Tập 1 Chân trời sáng tạo

Bài 1 trang 102 Toán lớp 10: Cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ đều khác vectơ $\vec{0}$ . Các khẳng định sau đúng hay sai?

a) Nếu hai vectơ $\vec{a}, \vec{b}$ cùng phương với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng phương.

b) Nếu hai vectơ $\vec{a}, \vec{b}$ cùng ngược hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng hướng.

Phương pháp giải:

Nhận xét về giá và hướng của hai vectơ $\vec{a}, \vec{b}$ với vectơ $\vec{c}$ để rút ra kết luận.

Lời giải:

+) Vectơ $\vec{a}$ cùng phương với vectơ $\vec{c}$ nên giá của vectơ $\vec{a}$ song song với giá của vectơ $\vec{c}$

+) Vectơ $\vec{b}$ cùng phương với vectơ $\vec{c}$ nên giá của vectơ $\vec{b}$ song song với giá của vectơ $\vec{c}$

Suy ra giá của vectơ $\vec{a}$ và vectơ $\vec{b}$ song song với nhau nên $\vec{a}$ và $\vec{b}$ cùng phương

Vậy khẳng định trên đúng

b) Giả sử vectơ $\vec{c}$ có hướng từ A sang B

+) Vectơ $\vec{a}$ ngược hướng với vectơ $\vec{c}$ nên giá của vectơ $\vec{a}$ song song với giá của vectơ $\vec{c}$ và có hướng từ B sang A

+) Vectơ $\vec{b}$ ngược hướng với vectơ $\vec{c}$ nên giá của vectơ $\vec{b}$ song song với giá của vectơ $\vec{c}$ và có hướng từ B sang A

Suy ra, hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng

Vậy khẳng định trên đúng

Bài 2 trang 102 Toán lớp 10: Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a.

a) Tính độ dài của các vectơ $\vec{A C}, \vec{B D}$ .

b) Tìm trong hình các cặp vectơ đối nhau và có độ dài bằng $\frac{a \sqrt{10}}{2}$ .

Phương pháp giải:

a) Bước 1: Tính độ dài AC, BD

Bước 2: Tính độ dài vectơ $| \vec{A B} | = A B$

b) Bước 1: Tìm các đoạn thẳng có độ dài là $\frac{a \sqrt{10}}{2}$

Bước 2: Từ các đoạn thẳng trên xác định các vecto cùng phương (giá song song hoặc trùng nhau) nhưng ngược hướng.

Lời giải:

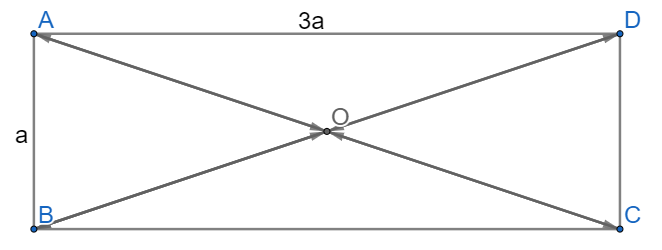
a) Ta có:

$A C = B D = \sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + {(3 a)}^{2}} = a \sqrt{10}$

+) $| \vec{A C} | = A C = a \sqrt{10}$

+) $| \vec{B D} | = B D = a \sqrt{10}$

b) O là giao điểm của hai đường chéo nên ta có:

$A O = O C = B O = O D = \frac{a \sqrt{10}}{2}$

Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng

Suy ra các cặp vectơ đối nhau và có độ dài bằng $\frac{a \sqrt{10}}{2}$ là:

$\vec{O A}$ và $\vec{O C}$ ; $\vec{A O}$ và $\vec{C O}$ ; $\vec{O B}$ và $\vec{O D}$ ; $\vec{B O}$ và $\vec{D O}$

Bài 3 trang 102 Toán lớp 10: Cho hình thoi ABCD đi có cạnh bằng a và có góc A bằng $60^{\circ}$ . Tìm độ dài của các vectơ sau: $\vec{p} = \vec{A B} + \vec{A D}; \vec{u} = \vec{A B} - \vec{A D}; \vec{v} = 2 \vec{A B} - \vec{A C}$ .

Phương pháp giải:

Quy tắc ba điểm $\vec{A B} = \vec{A O} + \vec{O B}$

Quy tắc hình bình hành $\vec{A B} + \vec{A D} = \vec{A C}$ (với ABCD là hình bình hành);

Quy tắc hiệu: $\vec{A B} - \vec{A C} = \vec{C B}$

Áp dụng các quy tắc trên để xác định vecto $\vec{p}, \vec{u}, \vec{v}$ rồi tính độ dài.

Lời giải:

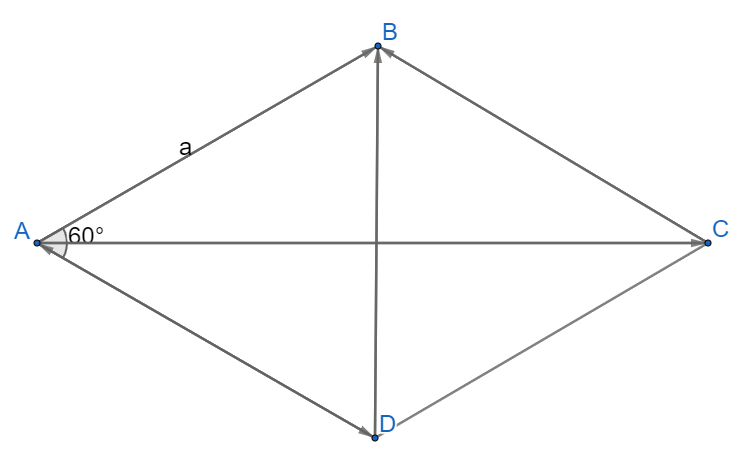
+) ABCD là hình thoi nên cũng là hình bình hành

Áp dụng quy tắc hình bình hành ta có:

$\vec{p} = \vec{A B} + \vec{A D} = \vec{A C}$

+) $\vec{u} = \vec{A B} - \vec{A D} = \vec{D B}$

+) $\vec{v} = 2 \vec{A B} - \vec{A C} = \vec{A B} + (\vec{A B} - \vec{A C}) = \vec{A B} + \vec{C B}$ $= \vec{A B} + \vec{D A} = \vec{D B}$

Bài 4 trang 102 Toán lớp 10: Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho $\vec{C E} = \vec{A N}$ (Hình 1).

Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC

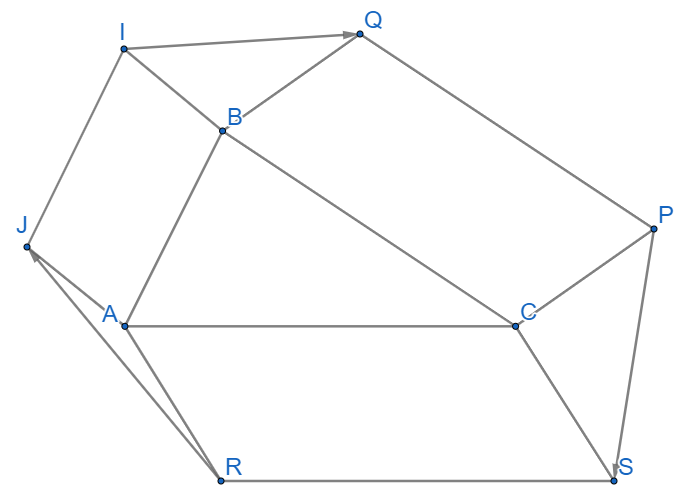
a) Tìm tổng của các vectơ $\vec{N C}$ và $\vec{M C}$ ; $\vec{A M}$ và $\vec{C D}$ ; $\vec{A D}$ và $\vec{N C}$ .

b) Tìm các vectơ hiệu: $\vec{N C} - \vec{M C}; \vec{A C} - \vec{B C}; \vec{A B} - \vec{M E}$ .

c) Chứng minh $\vec{A M} + \vec{A N} = \vec{A B} + \vec{A D}$ .

Phương pháp giải:

a) Chỉ ra các hình bình hành, từ đó suy ra các vectơ bằng nhau và vận dụng quy tắc hình bình hành.

b) Quy tắc hiệu: $\vec{A B} - \vec{A C} = \vec{C B}$ , quy tắc ba điểm $\vec{A B} = \vec{A O} + \vec{O B}$ và thay thế các vectơ bằng nhau $\vec{M E} = \vec{A D}$

c) Thay thế các vectơ bằng nhau $\vec{A N} = \vec{M C}$ ; sử dụng quy tắc hình bình hành $\vec{A B} + \vec{A D} = \vec{A C}$ (với ABCD là hình bình hành)

Lời giải:

a) Ta có: $\vec{C E} = \vec{A N} \Rightarrow C E / / A N$ và $C E = A N = N D = B M = M C$

Suy ra $\vec{M C} = \vec{C E}$

+) $\vec{N C} + \vec{M C} = \vec{N C} + \vec{C E} = \vec{N E}$

+) ABCD là hình bình hành nên $\vec{C D} = \vec{B A}$

$\vec{A M} + \vec{C D} = \vec{A M} + \vec{B A} = \vec{B M}$

+) Ta có $\vec{M C} = \vec{A N} \Rightarrow A M C N$ là hình bình hành nên $\vec{N C} = \vec{A M}$

$\vec{A D} + \vec{N C} = \vec{A D} + \vec{A M} = \vec{A E}$ (vì AMED là hình bình hành)

b) Ta có:

+) $\vec{N C} - \vec{M C} = \vec{N C} + \vec{C M} = \vec{N M}$

+) $\vec{A C} - \vec{B C} = \vec{A C} + \vec{C B} = \vec{A B}$

+) $\vec{A B} - \vec{M E} = \vec{A B} - \vec{A D} = \vec{A B} + \vec{D A} = \vec{D B}$

c) Ta có:

$\vec{A M} + \vec{A N} = \vec{A M} + \vec{M C} = \vec{A C}$

Áp dụng quy tắc hình bình hành vào hình bình hành ABCD ta có

$\vec{A B} + \vec{A D} = \vec{A C}$

Từ đó suy ra $\vec{A M} + \vec{A N} = \vec{A B} + \vec{A D}$ (đpcm)

Giải toán lớp 10 trang 103 Tập 1 Chân trời sáng tạo

Bài 5 trang 103 Toán lớp 10: Cho $\vec{a}, \vec{b}$ là hai vectơ khác vectơ $\vec{0}$ . Trong trường hợp nào thì đẳng thức sau đúng?

a) $|\vec{a} + \vec{b}| = |\vec{a}| + |\vec{b}|$ ;

b) $|\vec{a} + \vec{b}| = |\vec{a} - \vec{b}|$ .

Phương pháp giải:

Sử dụng tính chất ${\vec{a}}^{2} = | \vec{a} |^{2}$

Lời giải:

a) $| \vec{a} + \vec{b} | = | \vec{a} | + | \vec{b} | \Leftrightarrow {| \vec{a} + \vec{b} |}^{2} = {(| \vec{a} | + | \vec{b} |)}^{2}$

$\Leftrightarrow {(\vec{a} + \vec{b})}^{2} = {(| \vec{a} | + | \vec{b} |)}^{2} \Leftrightarrow {(\vec{a})}^{2} + 2 \vec{a} . \vec{b} + {(\vec{b})}^{2} = {| \vec{a} |}^{2} + 2. | \vec{a} | . | \vec{b} | + {| \vec{b} |}^{2}$

$\Leftrightarrow {| \vec{a} |}^{2} + 2 \vec{a} . \vec{b} + {| \vec{b} |}^{2} = {| \vec{a} |}^{2} + 2. | \vec{a} | . | \vec{b} | + {| \vec{b} |}^{2}$

$\Leftrightarrow 2 \vec{a} . \vec{b} = 2 | \vec{a} | . | \vec{b} |$

$\Leftrightarrow 2 | \vec{a} | . | \vec{b} | \cos (\vec{a}, \vec{b}) = 2 | \vec{a} | . | \vec{b} |$

$\Leftrightarrow \cos (\vec{a}, \vec{b}) = 1 \Leftrightarrow (\vec{a}, \vec{b}) = 0^{\circ}$

Vậy $| \vec{a} + \vec{b} | = | \vec{a} | + | \vec{b} | \Leftrightarrow \vec{a}, \vec{b}$ cùng hướng.

b) $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} | \Leftrightarrow {| \vec{a} + \vec{b} |}^{2} = {| \vec{a} - \vec{b} |}^{2}$

$\Leftrightarrow {(\vec{a} + \vec{b})}^{2} = {(\vec{a} - \vec{b})}^{2}$

$\Leftrightarrow {(\vec{a})}^{2} + 2 \vec{a} . \vec{b} + {(\vec{b})}^{2} = {(\vec{a})}^{2} - 2 \vec{a} . \vec{b} + {(\vec{b})}^{2}$

$\Leftrightarrow 2 \vec{a} . \vec{b} = - 2 \vec{a} . \vec{b} \Leftrightarrow 4 \vec{a} . \vec{b} = 0$

$\Leftrightarrow \vec{a} . \vec{b} = 0 \Leftrightarrow (\vec{a}, \vec{b}) = 90^{\circ}$

Vậy $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} | \Leftrightarrow \vec{a}, \vec{b}$ vuông góc với nhau.

Bài 6 trang 103 Toán lớp 10: Cho $| \vec{a} + \vec{b} | = 0$ . So sánh độ dài, phương và hướng của hai vectơ $\vec{a}$ và $\vec{b}$ .

Lời giải:

$| \vec{a} + \vec{b} | = 0 \Leftrightarrow \vec{a} + \vec{b} = \vec{0} \Leftrightarrow \vec{a} = - \vec{b}$

$\vec{a} = - \vec{b}$ suy ra hai vectơ $\vec{a}$ và $\vec{b}$ là hai vecto đối nhau nên chúng cùng phương, ngược hướng và có độ dài bằng nhau.

Bài 7 trang 103 Toán lớp 10: Cho bốn điểm A, B, C, D. Chứng minh rằng $\vec{A B} = \vec{C D}$ khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.

Phương pháp giải:

Chứng minh thông qua ABCD là hình bình hành.

Lời giải:

Với 4 điểm A, B, C, D ta có: $\vec{A B} = \vec{C D}$ khi và chỉ khi tứ giác ABDC là hình bình hành

Theo tính chất của hình bình hành thì giao điểm của hai đường chéo là trung điểm của mỗi đường và ngược lại.

Nói cách khác: trung điểm của hai đoạn thẳng AD và BC trùng nhau.

Vậy ta có điều phải chứng minh.

Bài 8 trang 103 Toán lớp 10: Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng $\vec{R J} + \vec{I Q} + \vec{P S} = \vec{0}$

Phương pháp giải:

Bước 1: Sử dụng quy tắc ba điểm $\vec{A B} = \vec{A O} + \vec{O B}$

Bước 2: Xác định các cặp vectơ đối nhau từ các hình bình hành $\vec{A B}$ và $\vec{C D}$ là hai vectơ đối nhau với ABCD là hình bình hành

Bước 3: Sử dụng tính chất của vectơ đối $\vec{A B}$ và $\vec{C D}$ là hai vectơ đối nhau thì $\vec{A B} + \vec{C D} = \vec{0}$

Lời giải:

$\vec{R J} + \vec{I Q} + \vec{P S} = (\vec{R A} + \vec{A J}) + (\vec{I B} + \vec{B Q}) + (\vec{P C} + \vec{C S})$

$= (\vec{R A} + \vec{C S}) + (\vec{A J} + \vec{I B}) + (\vec{B Q} + \vec{P C}) = \vec{0} + \vec{0} + \vec{0} = \vec{0}$ (đpcm)

Bài 9 trang 103 Toán lớp 10: Một chiếc máy bay được biết là đang bay về phía bắc với tốc độ 45 m/s, mặc dù vận tốc của nó so với mặt đất là 38 m/s theo hướng nghiêng một góc 20° về phía tây bắc (Hình 2). Tính tốc độ của gió.

Phương pháp giải:

Bước 1: Dựa vào hình 2 xác định các vectơ tương ứng với vận tốc của máy bay, vận tốc so với mặt đất

Bước 2: Dựa vào mối liên hệ giữa các vectơ đã cho $\vec{v} = \vec{v_{1}} + \vec{v_{2}}$ xác định vectơ tương ứng với vận tốc gió

Bước 3: Áp dụng định lý cosin tìm tốc độ của gió

Lời giải:

Từ giả thiết ta có:

+) Vectơ tương ứng với vận tốc máy bay là vectơ $\vec{v_{1}}$

+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ $\vec{v}$

+) Vectơ tương ứng với vận tốc gió là vectơ $\vec{v_{2}}$

Ta có : $| \vec{v_{1}} | = 45; | \vec{v} | = 38; (\vec{v_{1}}, \vec{v}) = 20^{\circ}$

Áp dụng định lý cosin ta có:

$| \vec{v_{2}} | = \sqrt{{| \vec{v} |}^{2} + {| \vec{v_{1}} |}^{2} - 2 | \vec{v} | . | \vec{v_{1}} | . \cos (\vec{v}, \vec{v_{1}})}$

$= \sqrt{38^{2} + 45^{2} - 2.38.45. \cos 20^{\circ}} ≃ 16$ (m/s)

Vậy tốc độ của gió gần bằng 16 m/s

Bài 10 trang 103 Toán lớp 10: Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng $\vec{M D} + \vec{M E} + \vec{M F} = \frac{3}{2} \vec{M O}$

Phương pháp giải:

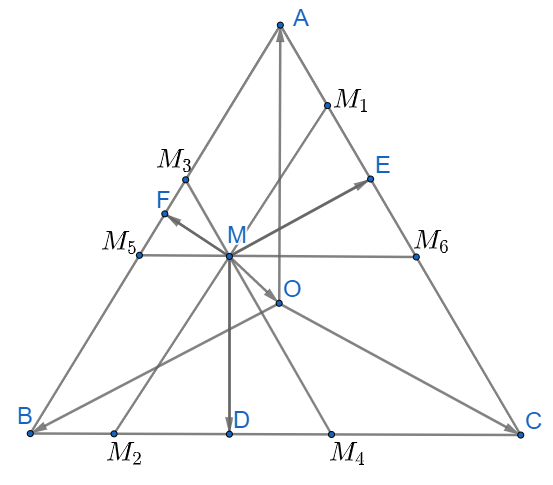
Bước 1: Qua M kẻ các đường thẳng song song với AB, AC, BC

Bước 2: Xác định các tam giác đều, hình bình hành sau đó áp dụng vào biểu thức vectơ, trong tam giác đều thì đường cao vừa là trung tuyến, quy tắc hình bình hành $\vec{A B} + \vec{A D} = \vec{A C}$ (với ABCD là hình bình hành)

Bước 3: Sử dụng quy tắc ba điểm $\vec{A B} = \vec{A O} + \vec{O B}$ , tính chất trọng tâm của tam giác $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ (với G là trọng tâm của tam giác ABC)

Lời giải:

$\vec{M D} + \vec{M E} + \vec{M F} = (\vec{M O} + \vec{O D}) + (\vec{M O} + \vec{O E}) + (\vec{M O} + \vec{O F})$

Qua M kẻ các đường thẳng $M_{1} M_{2} / / A B; M_{3} M_{4} / / A C; M_{5} M_{6} / / B C$

Từ đó ta có: $\hat{M M_{1} M_{6}} = \hat{M M_{6} M_{1}} = \hat{M M_{4} M_{2}} = \hat{M M_{2} M_{4}} = \hat{M M_{3} M_{5}} = \hat{M M_{5} M_{3}} = 60^{\circ}$

Suy ra các tam giác $Δ M M_{3} M_{5}, Δ M M_{1} M_{6}, Δ M M_{2} M_{4}$ đều

Áp dụng tính chất trung tuyến $\vec{A M} = \frac{1}{2} (\vec{A B} + \vec{A C})$ (với M là trung điểm của BC) ta có:

$\vec{M E} = \frac{1}{2} (\vec{M M_{1}} + \vec{M M_{6}}); \vec{M D} = \frac{1}{2} (\vec{M M_{2}} + \vec{M M_{4}}); \vec{M F} = \frac{1}{2} (\vec{M M_{3}} + \vec{M M_{5}})$

$\Rightarrow \vec{M D} + \vec{M E} + \vec{M F} = \frac{1}{2} (\vec{M M_{2}} + \vec{M M_{4}}) + \frac{1}{2} (\vec{M M_{1}} + \vec{M M_{6}}) + \frac{1}{2} (\vec{M M_{3}} + \vec{M M_{5}})$

Ta có: các tứ giác $A M_{3} M M_{1}; C M_{4} M M_{6}; B M_{2} M M_{5}$ là hình bình hành

Áp dụng quy tắc hình bình hành ta có

$\vec{M D} + \vec{M E} + \vec{M F} = \frac{1}{2} (\vec{M M_{2}} + \vec{M M_{4}}) + \frac{1}{2} (\vec{M M_{1}} + \vec{M M_{6}}) + \frac{1}{2} (\vec{M M_{3}} + \vec{M M_{5}})$

$= \frac{1}{2} (\vec{M M_{1}} + \vec{M M_{3}}) + \frac{1}{2} (\vec{M M_{2}} + \vec{M M_{5}}) + \frac{1}{2} (\vec{M M_{4}} + \vec{M M_{6}})$

$= \frac{1}{2} \vec{M A} + \frac{1}{2} \vec{M B} + \frac{1}{2} \vec{M C} = \frac{1}{2} (\vec{M A} + \vec{M B} + \vec{M C})$

$= \frac{1}{2} ((\vec{M O} + \vec{O A}) + (\vec{M O} + \vec{O B}) + (\vec{M O} + \vec{O C}))$

$= \frac{1}{2} (3 \vec{M O} + (\vec{M A} + \vec{M B} + \vec{M C})) = \frac{3}{2} \vec{M O}$ (đpcm)

Vậy $\vec{M D} + \vec{M E} + \vec{M F} = \frac{3}{2} \vec{M O}$

Bài 11 trang 103 Toán lớp 10: Một xe goòng được kéo bởi một lực $\vec{F}$ có độ lớn là 50 N, di chuyển theo quãng đường từ A đến B có chiều dài 200 m. Cho biết góc giữa $\vec{F}$ và $\vec{A B}$ là 30° và $\vec{F}$ được phân tích thành 2 lực $\vec{F_{1}}, \vec{F_{2}}$ (Hình 3). Tính công sinh bởi các lực $\vec{F_{1}}, \vec{F_{2}}$ và $\vec{F_{2}}$ .

Một xe goòng được kéo bởi một lực F có độ lớn là 50 N

Phương pháp giải:

Bước 1: Sử dụng các tính chất trong tam giác vuông xác định độ lớn của các lực

Bước 2: Xác định góc giữa các lực và hướng dịch chuyển

Bước 3: Sử dụng công thức $A = \vec{F} . \vec{d}$ (với $\vec{d}$ là vectơ thể hiện độ dịch chuyển và quãng đường mà vật đi được)

Lời giải:

Ta xác định được các độ lớn:

$| \vec{F} | = 50, | \vec{F_{2}} | = | \vec{F} | \cos 30^{\circ} = 50. \frac{\sqrt{3}}{2} = 25 \sqrt{3}, | \vec{F_{1}} | = | \vec{F} | . \sin 30^{\circ} = 50. \frac{1}{2} = 25$ (N)

Dựa vào hình vẽ ta có: $(\vec{F}, \vec{d}) = 30^{\circ}, (\vec{F_{1}}, \vec{d}) = 90^{\circ}, (\vec{F_{2}}, \vec{d}) = 0^{\circ}$

Áp dụng công thức tính công sinh ra bởi lực $A = \vec{F} . \vec{d}$ ta có:

$A = \vec{F} . \vec{d} = | \vec{F} | | \vec{d} | \cos (\vec{F}, \vec{d}) = 50.200. \cos 30^{\circ} = 5000 (J)$

$A_{1} = \vec{F_{1}} . \vec{d} = | \vec{F_{1}} | | \vec{d} | \cos (\vec{F_{1}}, \vec{d}) = 25.200. \cos 90^{\circ} = 0 (J)$

$A_{2} = \vec{F_{2}} . \vec{d} = | \vec{F_{2}} | | \vec{d} | \cos (\vec{F_{2}}, \vec{d}) = 25 \sqrt{3} .200 . \cos 0^{\circ} = 5000 \sqrt{3} (J)$

Bài 12 trang 103 Toán lớp 10: Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên, dòng chảy của nước trên con sông đó chảy với tốc độ 1,20 m/s về hướng bên phải. Gọi $\vec{v_{1}}, \vec{v_{2}}, \vec{v}$ lần lượt là vận tốc của thuyền so với dòng nước, vận tốc của dòng nước so với bờ và vận tốc của thuyền so với bờ.

a) Tính độ dài của các vectơ $\vec{v_{1}}, \vec{v_{2}}, \vec{v}$ .

b) Tốc độ dịch chuyển của thuyền so với bờ là bao nhiêu?

c) Hướng di chuyển của thuyền lệch một góc bao nhiêu so với bờ?

Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s

Phương pháp giải:

a) Sử dụng tính chất trong tam giác vuông $c^{2} = a^{2} + b^{2}$ (với c là cạnh huyền của tam giác vuông và a, b là cạnh góc vuông)

b) Chỉ ra kết quả độ dài vectơ $\vec{v}$ đã tính được ở câu a)

c) Sử dụng tính chất trong tam giác vuông $\sin B = \frac{a}{c}$ (với c là cạnh huyền của tam giác vuông và a, b là cạnh góc vuông)

Lời giải:

a) Ta có:

$| \vec{v_{1}} | = 0, 75; | \vec{v_{2}} | = 1, 20$

Dựa vào hình vẽ ta thấy $\vec{v} = \vec{v_{1}} + \vec{v_{2}}$ và $\vec{v_{1}} ⊥ \vec{v_{2}}$

Áp dụng tính chất trong tam giác vuông ta có: ${| \vec{v} |}^{2} = {| \vec{v_{1}} |}^{2} + {| \vec{v_{2}} |}^{2} \Rightarrow | \vec{v} | = \sqrt{{| \vec{v_{1}} |}^{2} + {| \vec{v_{2}} |}^{2}} = \sqrt{0, 75^{2} + 1, 2^{2}} = \frac{3 \sqrt{89}}{20}$

b) Tốc độ dịch chuyển của thuyền so với bờ là $\frac{3 \sqrt{89}}{20}$ m/s

c) Nước có hướng dichuyển song song với bờ nên hướng di chuyển của thuyền

so với bờ tương đương với hướng di chuyển của thuyền so với nước

Suy ra góc lệch giữa hướng di chuyển của thuyền và bờ là $(\vec{v}, \vec{v_{2}})$

Ta có: $\sin (\vec{v}, \vec{v_{2}}) = \frac{| \vec{v_{1}} |}{| \vec{v} |} = \frac{0, 75}{\frac{3 \sqrt{89}}{20}} = \frac{5 \sqrt{89}}{89} \Rightarrow (\vec{v}, \vec{v_{2}}) ≃ 32^{\circ}$

Vậy hướng di chuyển của thuyền lệch một góc $32^{\circ}$ so với bờ

Lý thuyết Chương 5: Vectơ

1. Định nghĩa vectơ

Vectơ là một đoạn thẳng có hướng, nghĩa là đã chỉ ra điểm đầu và điểm cuối.

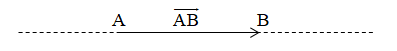
+ Vectơ có điểm đầu là A, điểm cuối là B được kí hiệu là $\vec{A B}$
, đọc là vectơ $\vec{A B}$ .

+ Đường thẳng đi qua hai điểm A và B gọi là giá của vectơ $\vec{A B}$ .

+ Độ dài của đoạn thẳng AB gọi là độ dài của $\vec{A B}$ và được kí hiệu là $|\vec{A B}|$ . Như vậy ta có $|\vec{A B}| = A B$ .

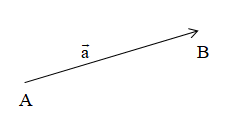
Chú ý: Một vectơ khi không cần chỉ rõ điểm đầu và điểm cuối có thể viết là $\vec{a}, \vec{b}, \vec{x}, \vec{y}, ...$

2. Hai vectơ cùng phương, cùng hướng

Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Ví dụ: Tìm các vectơ cùng phương trong hình bên dưới.

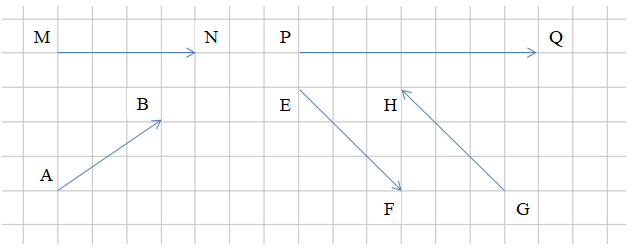
Hướng dẫn giải

Trong hình trên, ta có:

+) $\vec{M N}$ có giá là đường thẳng MN, $\vec{P Q}$ có giá là đường thẳng PQ, mà hai đường thẳng MN và PQ trùng nhau.

Do đó $\vec{M N}$ và $\vec{P Q}$ là hai vectơ cùng phương vì chúng có giá trùng nhau.

+) Ta có: $\vec{E F}$ có giá là đường thẳng EF, $\vec{G H}$ có giá là đường thẳng GH, mà hai đường thẳng EF và GH song song với nhau.

Do đó $\vec{E F}$ và $\vec{G H}$ là hai vectơ cùng phương vì chúng có giá song song.

Chú ý:

+ Trong hình trên, hai vectơ $\vec{M N}$ và $\vec{P Q}$ cùng phương và có cùng hướng đi từ trái sang phải. Ta nói $\vec{M N}$ và $\vec{P Q}$ là hai vectơ cùng hướng.

+ Hai vectơ $\vec{E F}$ và $\vec{G H}$ cùng phương nhưng ngược hướng với nhau ( $\vec{E F}$ có hướng từ trên xuống dưới và $\vec{G H}$ có hướng từ dưới lên trên). Ta nói hai vectơ $\vec{E F}$ và $\vec{G H}$ là hai vectơ ngược hướng.

Nhận xét:

+ Hai vectơ cùng phương chỉ có thể cùng hướng hoặc ngược hướng.

+ Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ $\vec{A B}$ và $\vec{A C}$ cùng phương.

Giải thích: Ta thấy nếu ba điểm A, B, C thẳng hàng thì hai vectơ $\vec{A B}$ và $\vec{A C}$ có giá trùng nhau nên chúng cùng phương. Ngược lại, nếu hai vectơ $\vec{A B}$ và $\vec{A C}$ cùng phương thì ta suy ta hai đường thẳng AB và AC phải song song hoặc trùng nhau. Mà hai đường thẳng này có điểm A là điểm chung, do đó đường thẳng AB và AC trùng nhau. Khi đó ta có ba điểm A, B, C thẳng hàng. Vì vậy, ba điểm A, B, C thẳng hàng khi và chỉ khi hai vectơ $\vec{A B}$ và $\vec{A C}$ cùng phương.

3. Vectơ bằng nhau – Vectơ đối nhau

Hai vectơ $\vec{a}$ và $\vec{b}$ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu $\vec{a} = \vec{b}$ .

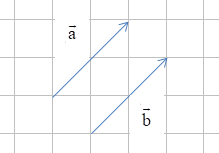
Hai vectơ $\vec{a}$ và $\vec{b}$ được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài, kí hiệu $\vec{a} = - \vec{b}$ . Khi đó vectơ $\vec{b}$ được gọi là vectơ đối của vectơ $\vec{a}$ .

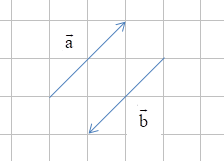
Chú ý:

+ Cho vectơ $\vec{a}$ và điểm O, ta luôn tìm được một điểm A duy nhất sao cho $\vec{O A} = \vec{a}$ . Khi đó độ dài của $\vec{a}$ là độ dài đoạn thẳng OA, kí hiệu là $|\vec{a}|$ .

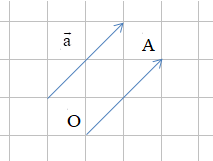
+ Cho đoạn thẳng MN, ta luôn có $\vec{N M} = - \vec{M N}$ .

4. Vectơ-không

Vectơ có điểm đầu và điểm cuối trùng nhau gọi là vectơ-không, kí hiệu là $\vec{0}$ .

Chú ý:

+ Quy ước: vectơ-không có độ dài bằng 0.

+ Vectơ-không luôn cùng phương, cùng hướng với mọi vectơ.

+ Mọi vectơ-không đều bằng nhau: $\vec{0} = \vec{A A} = \vec{B B} = \vec{C C} = ...$ , với mọi điểm A, B, C,...

+ Vectơ đối của vectơ-không là chính nó.

5. Tổng của hai vectơ

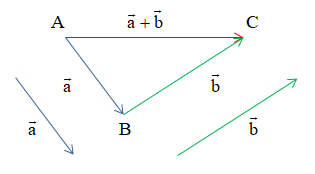
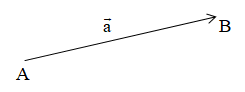
Cho hai vectơ $\vec{a}$ và $\vec{b}$ . Từ một điểm A tùy ý, lấy hai điểm B, C sao cho $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ . Khi đó $\vec{A C}$ được gọi là tổng của hai vectơ $\vec{a}$ và $\vec{b}$ và được kí hiệu là $\vec{a} + \vec{b}$ .

Vậy $\vec{a} + \vec{b} = \vec{A B} + \vec{B C} = \vec{A C}$ .

Phép toán tìm tổng của hai vectơ được gọi là phép cộng vectơ.

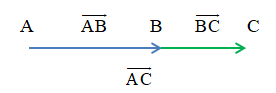
Quy tắc ba điểm

Với ba điểm M, N, P, ta có $\vec{M N} + \vec{N P} = \vec{M P}$ .

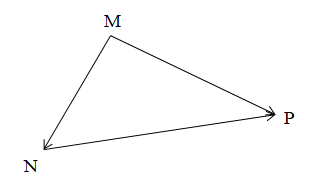Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.

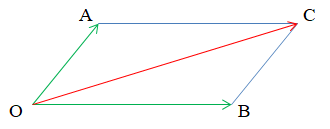
Quy tắc hình bình hành

Nếu OACB là hình bình hành thì ta có $\vec{O A} + \vec{O B} = \vec{O C}$ .

6. Tính chất của phép cộng các vectơ

Phép cộng vectơ có các tính chất sau:

+ Tính chất giao hoán: $\vec{a} + \vec{b} = \vec{b} + \vec{a}$ .

+ Tính chất kết hợp: $(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$ .

+ Với mọi $\vec{a}$ , ta luôn có: $\vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a}$ .

Chú ý: Từ tính chất kết hợp, ta có thể xác định được tổng của ba vectơ $\vec{a}, \vec{b}, \vec{c}$ ,kí hiệu là $\vec{a} + \vec{b} + \vec{c}$ với $\vec{a} + \vec{b} + \vec{c} = (\vec{a} + \vec{b}) + \vec{c}$ .

Chú ý: Cho vectơ tùy ý $\vec{a} = \vec{A B}$ .

Ta có $\vec{a} + (- \vec{a}) = \vec{A B} + (- \vec{A B}) = \vec{A B} + \vec{B A} = \vec{A A} = \vec{0}$ .

Tổng hai vectơ đối nhau luôn bằng vectơ-không: $\vec{a} + (- \vec{a}) = \vec{0}$ .

7. Hiệu của hai vectơ

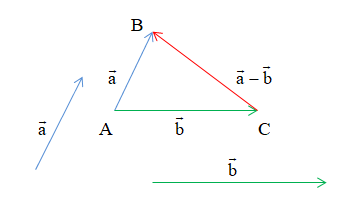
Cho hai vectơ $\vec{a}$ và $\vec{b}$ . Hiệu của hai vectơ $\vec{a}$ và $\vec{b}$ là vectơ $\vec{a} + (- \vec{b})$ và kí hiệu là $\vec{a} - \vec{b}$ .

Phép toán tìm hiệu của hai vectơ được gọi là phép trừ vectơ.

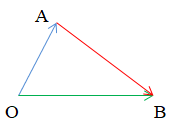
Chú ý: Cho ba điểm O, A, B, ta có: $\vec{O B} - \vec{O A} = \vec{A B}$ .

8. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác

Điểm M là trung điểm của đoạn thẳng AB khi và chỉ khi $\vec{M A} + \vec{M B} = \vec{0}$ .

Điểm G là trọng tâm của tam giác ABC khi và chỉ khi $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ .

9. Tích của một số với một vectơ và các tính chất

Cho số k ≠ 0 và $\vec{a} \neq \vec{0}$ . Tích của số k với $\vec{a} \neq \vec{0}$ là một vectơ, kí hiệu là $k \vec{a}$ .

Vectơ $k \vec{a}$ cùng hướng với $\vec{a}$ nếu k > 0, ngược hướng với $\vec{a}$ nếu k < 0 và có độ dài bằng $|k| . |\vec{a}|$ .

Ta quy ước $0 \vec{a} = \vec{0}$ và $k \vec{0} = \vec{0}$ .

Người ta còn gọi tích của một số với một vectơ là tích của một vectơ với một số.

Tính chất:

Với hai vectơ $\vec{a}$ và $\vec{b}$ bất kì, với mọi số thực h và k, ta có:

+) $k (\vec{a} + \vec{b}) = k \vec{a} + k \vec{b}$ ;

+) $(h + k) \vec{a} = h \vec{a} + k \vec{a}$ ;

+) $h (k \vec{a}) = (h k) \vec{a}$ ;

+) $1. \vec{a} = \vec{a}$ ;

+) $(- 1) . \vec{a} = - \vec{a}$ .

10. Điều kiện để hai vectơ cùng phương

Hai vectơ $\vec{a}$ và $\vec{b}$ ( $\vec{b} \neq \vec{0}$ ) cùng phương khi và chỉ khi có số k sao cho $\vec{a} = k \vec{b}$ .

Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k ≠ 0 để $\vec{A B} = k \vec{A C}$ .

Chú ý: Cho hai vectơ $\vec{a}$ và $\vec{b}$ không cùng phương. Với mỗi $\vec{c}$ luôn tồn tại duy nhất cặp số thực (m; n) sao cho $\vec{c} = m \vec{a} + n \vec{b}$ .

11. Góc giữa hai vectơ

Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác $\vec{0}$ . Từ một điểm O bất kì ta vẽ $\vec{O A} = \vec{a}$ , $\vec{O B} = \vec{b}$ .

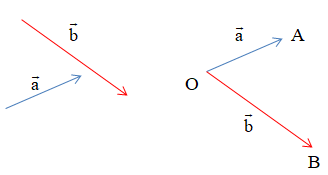
Góc $\hat{A O B}$ với số đo từ 0° đến 180° được gọi là góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ .

Ta kí hiệu góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ là $(\vec{a}, \vec{b})$ .

Nếu $(\vec{a}, \vec{b}) = 90 °$ thì ta nói rằng $\vec{a}$ và $\vec{b}$ vuông góc với nhau, kí hiệu $\vec{a} ⊥ \vec{b}$ .

Chú ý:

+ Từ định nghĩa, ta có $(\vec{a}, \vec{b}) = (\vec{b}, \vec{a})$ .

+ Góc giữa hai vectơ cùng hướng và khác $\vec{0}$ luôn bằng 0°.

+ Góc giữa hai vectơ ngược hướng và khác $\vec{0}$ luôn bằng 180°.

+ Trong trường hợp có ít nhất một trong hai vectơ $\vec{a}$ hoặc $\vec{b}$ là $\vec{0}$ thì ta quy ước số đo góc giữa hai vectơ đó là tùy ý (từ 0° đến 180°).

12. Tích vô hướng của hai vectơ

Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác $\vec{0}$ .

Tích vô hướng của $\vec{a}$ và $\vec{b}$ là một số, kí hiệu là $\vec{a} . \vec{b}$ , được xác định bởi công thức: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$ .

Chú ý:

a) Trường hợp có ít nhất một trong hai vectơ $\vec{a}$ và $\vec{b}$ bằng $\vec{0}$ , ta quy ước $\vec{a} . \vec{b} = 0$ .

b) Với hai vectơ $\vec{a}$ và $\vec{b}$ , ta có $\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} . \vec{b} = 0$ .

c) Khi $\vec{a} = \vec{b}$ thì tích vô hướng $\vec{a} . \vec{b}$ được kí hiệu là ${\vec{a}}^{2}$ và được gọi là bình phương vô hướng của vectơ $\vec{a}$ .

Ta có ${\vec{a}}^{2} = |\vec{a}| . |\vec{a}| . \cos 0 ° = {|\vec{a}|}^{2}$ . Vậy bình phương vô hướng của một vectơ luôn bằng bình phương độ dài của vectơ đó.

Chú ý: Trong Vật lí, tích vô hướng của và biểu diễn công A sinh bởi lực khi thực hiện độ dịch chuyển . Ta có công thức $A = \vec{F} . \vec{d}$

13. Tính chất của tích vô hướng

Với ba vectơ $\vec{a}, \vec{b}, \vec{c}$ bất kì và mọi số k, ta có:

$\vec{a} . \vec{b} = \vec{b} . \vec{a}$ ; $\vec{a} . (\vec{b} + \vec{c}) = \vec{a} . \vec{b} + \vec{a} . \vec{c}$ ; $(k \vec{a}) . \vec{b} = k (\vec{a} . \vec{b}) = \vec{a} . (k \vec{b})$ .