Với lời giải SBT Toán 10 trang 46 Tập 1 chi tiết trong Bài 1: Hàm số và đồ thị sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 1: Hàm số và đồ thị

Bài 3 trang 46 SBT Toán 10 Tập 1: Trong kinh tế thị trường, lượng cầu và lượng cung là hai khái niệm quan trọng. Lượng cầu chỉ khả năng về số lượng sản phẩm cần mua của bên mua (người dùng), tùy theo đơn giá bán sản phẩm; còn lượng cung chỉ khả năng cung cấp số lượng sản phẩm này cho thị trường của bên bán (nhà sản xuất) cũng phụ thuộc vào đơn giá sản phẩm.

Người ta khảo sát nhu cầu của thị trường đối với sản phẩm A theo đơn giá của sản phẩm này và thu được bảng sau:

a) Hãy cho biết tại sao bảng giá trị trên xác định một hàm số? Hãy tìm tập xác định và tập giá trị của hàm số đó (gọi là hàm cầu).

b) Giả sử lượng cung của sản phẩm A tuân theo công thức $y=f\left(x\right)=\frac{x^2}{50}$, trong đó x là đơn giá sản phẩm A và y là lượng cung ứng với đơn giá này. Hãy điền các giá trị của hàm số f(x) (gọi là hàm cung) vào bảng sau:

 c) Ta nói thị trường của một sản phẩm là cân bằng khi lượng cung và lượng cầu bằng nhau. Hãy tìm đơn giá x của sản phẩm A khi thị trường cân bằng.

Lời giải:

a) Từ bảng đã cho ta có thể thấy với mỗi mức đơn giá, đều có duy nhất một giá trị về lượng cầu. Do vậy bảng giá trị cho ở đề bài xác định một hàm số.

Hàm số này có tập xác định D = {10; 20; 40; 70; 90} và có tập giá trị T = {338; 288; 200; 98; 50}.

b) Ta có hàm cung: $y=f\left(x\right)=\frac{x^2}{50}$.

Với x = 10 thì $y=f\left(10\right)=\frac{{10}^2}{50}=2$;

Với x = 20 thì $y=f\left(20\right)=\frac{{20}^2}{50}=8$;

Với x = 40 thì $y=f\left(40\right)=\frac{{40}^2}{50}=32$;

Với x = 70 thì $y=f\left(70\right)=\frac{{70}^2}{50}=98$;

Với x = 90 thì $y=f\left(90\right)=\frac{{90}^2}{50}=162$;

Vậy ta điền được bảng sau:

 c) Từ hai bảng giá trị của lượng cung và lượng cầu, ta tìm được giá trị x = 70 thì lượng cung và lượng cầu đều bằng 98.

Vậy thị trường của sản phẩm A cân bằng khi đơn giá của sản phẩm A là 70 000 (đồng).

Bài 4 trang 46 SBT Toán 10 Tập 1: Tìm khoảng đồng biến, nghịch biến của các hàm số sau:

a) $f\left(x\right)=\frac{1}{-x-5}$;

b) f(x) = |3x – 1|.

Lời giải:

a) Tập xác định của hàm số là: D = ℝ \ {– 5}.

+ Xét khoảng (– ∞; – 5):

Lấy hai số x₁, x₂ tùy ý thuộc (– ∞; – 5) sao cho x₁ < x₂.

Ta có: $f\left(x_1\right)-f\left(x_2\right)=\frac{1}{-x_1-5}-\frac{1}{-x_2-5}$$=\frac{-x_2-5-\left(-x_1-5\right)}{\left(-x_1-5\right)\left(-x_2-5\right)}$$=\frac{x_1-x_2}{\left(x_1+5\right)\left(x_2+5\right)}$.

Vì x₁, x₂ ∈ (– ∞; – 5) nên x₁ + 5 < 0 và x₂ + 5 < 0.

Lại có: x₁ < x₂ nên x₁ – x₂ < 0.

Do đó, f(x₁) – f(x₂) $=\frac{x_1-x_2}{\left(x_1+5\right)\left(x_2+5\right)}$ < 0 hay f(x₁) < f(x₂).

Vậy hàm số đồng biến trên khoảng (– ∞; – 5). (1)

+ Xét khoảng (– 5; + ∞):

Lấy hai số x₃, x₄ tùy ý thuộc (– 5; + ∞) sao cho x₃ < x₄.

Ta có: $f\left(x_3\right)-f\left(x_4\right)=\frac{1}{-x_3-5}-\frac{1}{-x_4-5}$$=\frac{-x_4-5-\left(-x_3-5\right)}{\left(-x_3-5\right)\left(-x_4-5\right)}$$=\frac{x_3-x_4}{\left(x_3+5\right)\left(x_4+5\right)}$.

Vì x₃, x₄ ∈ (– 5; + ∞) nên x₃ + 5 > 0 và x₄ + 5 > 0.

Lại có: x₃ < x₄ nên x₃ – x₄ < 0.

Do đó, f(x₃) – f(x₄) $=\frac{x_3-x_4}{\left(x_3+5\right)\left(x_4+5\right)}$ < 0 hay f(x₁) < f(x₂).

Vậy hàm số đồng biến trên khoảng (– 5; + ∞). (2)

Từ (1) và (2) suy ra hàm số đã cho đồng biến trên các khoảng (– ∞; – 5) và (– 5; + ∞).

b) Với 3x – 1 ≥ 0 hay x ≥ $\frac{1}{3}$, ta có: |3x – 1| = 3x – 1.

Với 3x – 1 < 0 hay x < $\frac{1}{3}$, ta có: |3x – 1| = – (3x – 1) = – 3x + 1.

Khi đó ta có: $f\left(x\right)=\left\{\begin{array}{l}3x-1khix\ge \frac{1}{3}\\ -3x+1khix<\frac{1}{3}\end{array}\right.$.

Ta xét sự đồng biến, nghịch biến của hàm số g(x) = 3x – 1 trên khoảng $\left(\frac{1}{3};+\infty \right)$ và của hàm số h(x) = – 3x + 1 trên khoảng $\left(-\infty ;\frac{1}{3}\right)$.

+ Lấy hai số x₁, x₂ tùy ý thuộc khoảng $\left(\frac{1}{3};+\infty \right)$ sao cho x₁ < x­₂:

Ta có: f(x₁) – f(x₂) = (3x₁ – 1) – (3x₂ – 1) = 3(x₁ – x₂) < 0 (do x₁ < x₂ nên x₁ – x₂ < 0).

Suy ra f(x₁) < f(x₂).

Vậy hàm số g(x) đồng biến trên $\left(\frac{1}{3};+\infty \right)$ hay f(x) đồng biến trên $\left(\frac{1}{3};+\infty \right)$. (1)

+ Lấy hai số x₃, x₄ tùy ý thuộc khoảng $\left(-\infty ;\frac{1}{3}\right)$ sao cho x₃ < x₄:

Ta có: f(x₃) – f(x₄) = (– 3x₃ + 1) – (– 3x₄ + 1) = 3(x₄ – x₃) > 0 (do x₃ < x₄ nên x₄ – x₃ > 0).

Suy ra f(x₃) > f(x₄).

Vậy hàm số h(x) nghịch biến trên $\left(-\infty ;\frac{1}{3}\right)$ hay f(x) nghịch biến khoảng $\left(-\infty ;\frac{1}{3}\right)$. (2)

Từ (1) và (2) suy ra hàm số f(x) nghịch biến trên khoảng $\left(-\infty ;\frac{1}{3}\right)$ và đồng biến trên khoảng $\left(\frac{1}{3};+\infty \right)$.

Bài 5 trang 46 SBT Toán 10 Tập 1: Tìm khoảng đồng biến, nghịch biến của hàm số có đồ thị như sau:

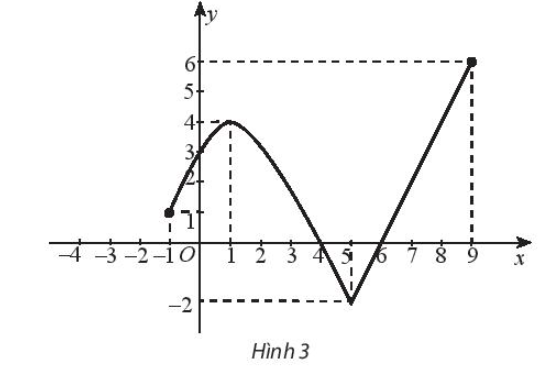
Lời giải:

Quan sát Hình 3 ta thấy:

- Đồ thị hàm số có dạng đi lên từ điểm có tọa độ (– 1; 1) đến điểm có tọa độ (1; 4) nên hàm số đồng biến trên khoảng (– 1; 1);

- Đồ thị hàm số có dạng đi xuống từ điểm có tọa độ (1; 4) đến điểm có tọa độ (5; – 2) nên hàm số nghịch biến trên khoảng (1; 5);

- Đồ thị hàm số có dạng đi lên từ điểm có tọa độ (5; – 2) đến điểm có tọa độ (9; 6) nên hàm số đồng biến trên khoảng (5; 9).

Vậy hàm số có đồ thị như Hình 3 đồng biến trên các khoảng (– 1; 1) và (5; 9), nghịch biến trên khoảng (1; 5).

Xem thêm các bài giải sách bài tập Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 45 Tập 1

Giải SBT Toán 10 trang 47 Tập 1

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của một góc từ 0 đến 180