Với lời giải SBT Toán 7 trang 116 Tập 1 chi tiết trong Bài tập cuối chương 4 sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài tập cuối chương 4

Bài 40* trang 116 SBT Toán 7 Tập 1: Quan sát Hình 50, trong đó vết bẩn đã xóa mất đỉnh O của góc xOy. Sử dụng định lí phát biểu trong Bài tập 26b, nêu cách vẽ đường thẳng đi qua điểm M và vuông góc với tia phân giác của góc xOy.

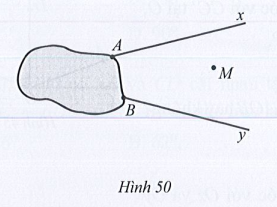
Lời giải

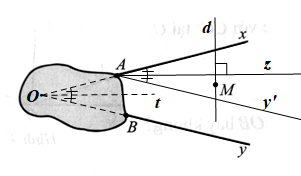
Kẻ Ay’ // By, khi đó ta có $\widehat{xA{y}^{\text{'}}}=\widehat{xOy}$ (hai góc đồng vị).

Vẽ tia Az là tia phân giác của góc xAy’.

Khi đó $\widehat{xAz}=\frac{1}{2}\widehat{xA{y}^{\text{'}}}=\frac{1}{2}\widehat{xOy}$

Vẽ tia Ot là tia phân giác của góc xOy.

Khi đó $\widehat{xOt}=\frac{1}{2}\widehat{xOy}$

Do đó $\widehat{xAz}=\widehat{xOt}$ (cùng bằng $\frac{1}{2}\widehat{xOy}$).

Mà $\widehat{xAz}$ và $\widehat{xOt}$ ở vị trí đồng vị nên Az // Ot.

Như vậy, qua điểm M kẻ đường thẳng d vuông góc với Az thì đường thẳng d là đường thẳng đi qua điểm M và vuông góc với tia phân giác của góc xOy (theo định lí phát biểu trong Bài tập 26b).

Bài 41 trang 116 SBT Toán 7 Tập 1: Quan sát Hình 51, biết Ox // HK, tia Ox là tia phân giác của góc yOK. Chứng minh hai góc OHK và OKH bằng nhau.

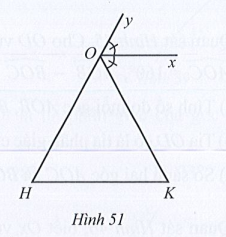
Lời giải

Vì Ox là tia phân giác của góc yOK nên $\widehat{xOy}=\widehat{xOK}$

Do Ox // HK nên ta có:

• $\widehat{xOy}=\widehat{OHK}$ (hai góc đồng vị);

• $\widehat{xOK}=\widehat{OKH}$ (hai góc so le trong).

Do đó $\widehat{OHK}=\widehat{OKH}$ (cùng bằng $\widehat{xOy}$ và $\widehat{xOK}$).

Vậy $\widehat{OHK}=\widehat{OKH}.$

Bài 42* trang 116 SBT Toán 7 Tập 1: Tìm số đo góc QRS trong Hình 52, biết aa’ // cc’.

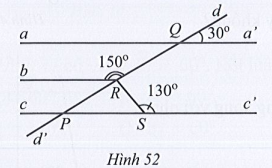
Lời giải

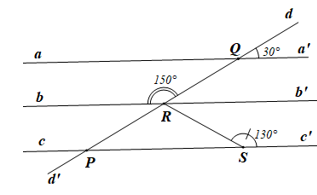
Kẻ Rb’ là tia đối của tia Rb (hình vẽ trên).

• Ta có $\widehat{QRb}+\widehat{QR{b}^{\text{'}}}=180°$ (hai góc kề bù)

Suy ra 

$$\begin{gathered} \widehat{QR{b}^{\text{'}}}=180°-\widehat{QRb} \\ =180°-150°=30°. \end{gathered}$$

• Do aa’ // cc’ nên $\widehat{dP{c}^{\text{'}}}=\widehat{dQ{a}^{\text{'}}}=30°$ (hai góc đồng vị)

Khi đó $\widehat{dP{c}^{\text{'}}}=\widehat{QR{b}^{\text{'}}}$ (cùng bằng 30°).

Mà $\widehat{dP{c}^{\text{'}}}$ và $\widehat{QR{b}^{\text{'}}}$ ở vị trí đồng vị nên bb’ // cc’.

Suy ra $\widehat{SR{b}^{\text{'}}}+\widehat{RS{c}^{\text{'}}}=180°$ (hai góc trong cùng phía).

Do đó 

$$\begin{gathered} \widehat{SR{b}^{\text{'}}}=180°-\widehat{RS{c}^{\text{'}}} \\ =180°-130°=50°. \end{gathered}$$

• Vì hai góc QRb’ và SRb’ là hai góc kề nhau nên:

$$\begin{gathered} \widehat{QRS}=\widehat{QR{b}^{\text{'}}}+\widehat{SR{b}^{\text{'}}} \\ =30°+50°=80°. \end{gathered}$$

Vậy $\widehat{QRS}°=80°.$

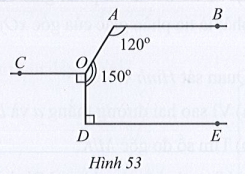
Bài 43* trang 116 SBT Toán 7 Tập 1: Cho Hình 53 có OC và DE cùng vuông góc với OD, $\widehat{BAO}=120°,\widehat{AOD}=150°.$Chứng tỏ rằng AB // OC // DE.

Lời giải

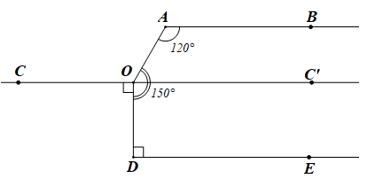
Kẻ OC’ là tia đổi của tia OC (hình vẽ trên).

• Do $\widehat{COD}=\widehat{ODE}$ (cùng bằng 90°).

Mà $\widehat{COD}$ và $\widehat{ODE}$ ở vị trí so le trong nên OC // DE.

Suy ra $\widehat{DO{C}^{\text{'}}}+\widehat{ODE}=180°$ (hai góc trong cùng phía)

Do đó 

$$\begin{gathered} \widehat{DO{C}^{\text{'}}}=180°-\widehat{ODE} \\ =180°-90°=90°. \end{gathered}$$

• Do hai góc AOC’ và DOC’ là hai góc kề nhau nên:

$\widehat{AOC’}+\widehat{DOC’}=\widehat{AOD}$

Suy ra 

$$\begin{gathered} \widehat{AOC’}=\widehat{AOD}-\widehat{DOC’} \\ =150°-90°=60°. \end{gathered}$$

• Ta có $\widehat{AOC}+\widehat{AO{C}^{\text{'}}}=180°$ (hai góc kề bù)

Suy ra 

$$\begin{gathered} \widehat{AOC}=180°-\widehat{AO{C}^{\text{'}}} \\ =180°-60°=120°. \end{gathered}$$

Do đó $\widehat{BAO}=\widehat{AOC}$ (cùng bằng 120°).

Mà $\widehat{BAO}$ và $\widehat{AOC}$ ở vị trí so le trong nên AB // OC.

Do OC // DE và AB // OC nên AB // OC // DE (hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau).

Vậy AB // OC // DE

Xem thêm các bài giải sách bài tập Toán 7 Cánh diều hay, chi tiết khác:

Giải SBT Toán 7 trang 114 Tập 1

Giải SBT Toán 7 trang 115 Tập 1