Với giải sách bài tập Toán 7 Bài 3: Hai đường thẳng song song sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài 3: Hai đường thẳng song song
Bài 16 trang 110 Toán 7 Tập 1: Quan sát Hình 28, biết a // b,
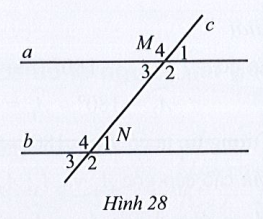
a) Nêu những cặp góc so le trong, những cặp góc đồng vị.
b) Tìm số đo mỗi góc còn lại của đỉnh M và N.
Lời giải:
a) Những cặp góc so le trong là: và và
Những cặp góc đồng vị là: và và và và
b)
– Tại đỉnh M:
• Vì và là hai góc đối đỉnh nên:
• Vì và là hai góc kề bù nên:
Suy ra
Vì và là hai góc đối đỉnh nên:
– Tại đỉnh N:
Vì a // b nên
• (hai góc so le trong).
• (hai góc đồng vị).
• (hai góc đồng vị).
• (hai góc so le trong).
Vậy
Bài 17 trang 110 Toán 7 Tập 1: Quan sát Hình 29, biết a // b, Tìm số đo mỗi góc của đỉnh A và B.
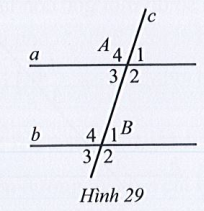
Lời giải:
– Tại đỉnh A:
• Ta có (hai góc kề bù).
Mà hay
Nên
Do đó
Suy ra
Khi đó
• (hai góc đối đỉnh).
• (hai góc đối đỉnh).
– Tại đỉnh B: Vì a // b nên ta có:
• (hai góc so le trong).
• (hai góc đồng vị).
• (hai góc đồng vị).
• (hai góc so le trong).
Vậy
Bài 18 trang 110 Toán 7 Tập 1: Tìm số đo mỗi góc B1, B2, B3, B4 trong Hình 30, biết m // n.
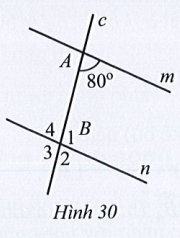
Lời giải:
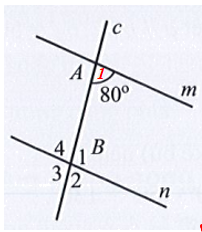
Giả sử như hình vẽ.
Vì m // n nên ta có:
• (hai góc so le trong);
• (hai góc đồng vị).
• (hai góc trong cùng phía)
Suy ra
Do đó (hai góc đối đỉnh).
Vậy
Bài 19 trang 110 Toán 7 Tập 1: Quan sát Hình 31, biết Tìm số đo mỗi góc còn lại của đỉnh M và N.
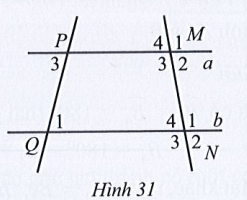
Lời giải:
+) Ta có: (hai góc đối đỉnh).
Vì và là hai góc kề bù nên ta có:
Suy ra
Do đó (hai góc đối đỉnh).
+) Ta có mà hai góc này ở vị trí so le trong
Nên PM // QN.
Do đó:
• (hai góc so le trong).
• (hai góc đồng vị).
• (hai góc đồng vị).
• (hai góc so le trong).
Vậy và
Bài 20 trang 110 Toán 7 Tập 1: Tìm số đo x, y trong Hình 32.
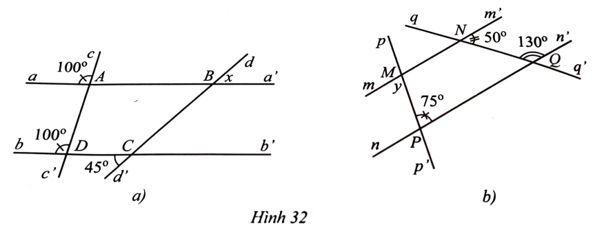
Lời giải:
a) Ta có (cùng bằng 100°).
Mà hai góc này ở vị trí đồng vị.
Do đó aa' // bb'.
Suy ra (hai góc do le ngoài).
Vậy x = 45°.
b) Vì và là hai góc kề bù nên ta có:
Suy ra
Do đó (cùng bằng 50°).
Mà hai góc này ở vị trí so le trong nên mm' // nn'.
Suy ra
Vậy y = 75°.
Bài 21 trang 111 Toán 7 Tập 1: Tìm số đo góc BCD trong Hình 33.
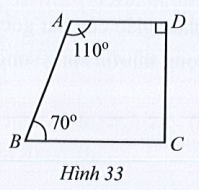
Lời giải:
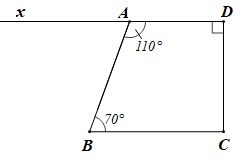
Vẽ tia Ax là tia đối của tia AD.
Khi đó và là hai góc kề bù nên ta có:
Suy ra
Do đó (cùng bằng 70°).
Mà hai góc này ở vị trí so le trong nên Dx // Cy.
Suy ra (hai góc trong cùng phía)
Do đó
Vậy
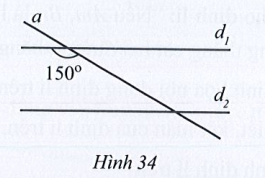
Lời giải:
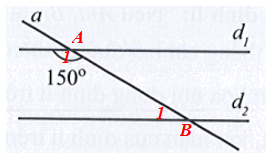
Giả sử là góc tù được tạo bởi đường thẳng a và đường thẳng d1;
là góc nhọn được tạo bởi đường thẳng a và đường thẳng d2.
Vì d1 // d2 nên (hai góc trong cùng phía).
Do đó
Vậy góc nhọn được tạo bởi đường thẳng a và đường thẳng d2 bằng 30°.
Bài 23 trang 111 Toán 7 Tập 1: Quan sát Hình 35, biết xx' // yy' // zz'. Chứng tỏ rằng
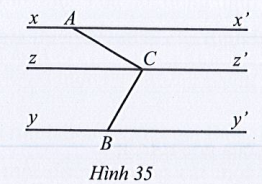
Lời giải:
Vì xx' // zz' nên (hai góc so le trong).
Vì yy' // zz' nên (hai góc so le trong).
Mặt khác: và là hai góc kề nhau
Nên
Do đó
Vậy
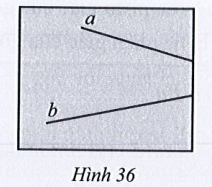
Lời giải:
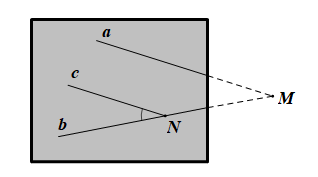
Giả sử đường thẳng a và đường thẳng b cắt nhau tại M nằm ngoài tờ giấy.
Khi đó góc nhọn tạo bởi hai đường thẳng a và b là
Trên đường thẳng b ta lấy điểm N, kẻ Nc // a sao cho là góc nhọn (hình vẽ).
Vì Nc // a nên (hai góc đồng vị).
Do đó ta đo góc bNc sẽ suy ra số đo của góc được tạo bởi hai đường thẳng a và b.
Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 2 : Tia phân giác của một góc
Bài 3 : Hai đường thẳng song song
Bài 1 : Thu thập, phân loại và biểu diễn dữ liệu
Lý thuyết Hai đường thẳng song song
1. Hai góc đồng vị. Hai góc so le trong

Đường thẳng c cắt hai đường thẳng a, b lần lượt tại điểm A, B.
Khi đó, ta thấy:
+ Góc A1 và góc B1 ở “cùng một phía” của đường thẳng c.
+ Góc A1 ở “phía trên” đường thẳng a. Góc B1 cũng ở “phía trên” đường thẳng b.
Hai góc A1 và B1 ở vị trí như thế được gọi là hai góc đồng vị.
 + Góc A3 và góc B1 ở “hai phía” của đường thẳng c.
+ Góc A3 và góc B1 ở “hai phía” của đường thẳng c.
+ Góc A3 ở “phía dưới” của đường thẳng a. Góc B1 lại ở “phía trên” của đường thẳng b.
Hai góc A3 và B1 ở vị trí như thế gọi là hai góc so le trong.
Ví dụ: Kể tên các cặp góc so le trong và đồng vị trong hình sau:
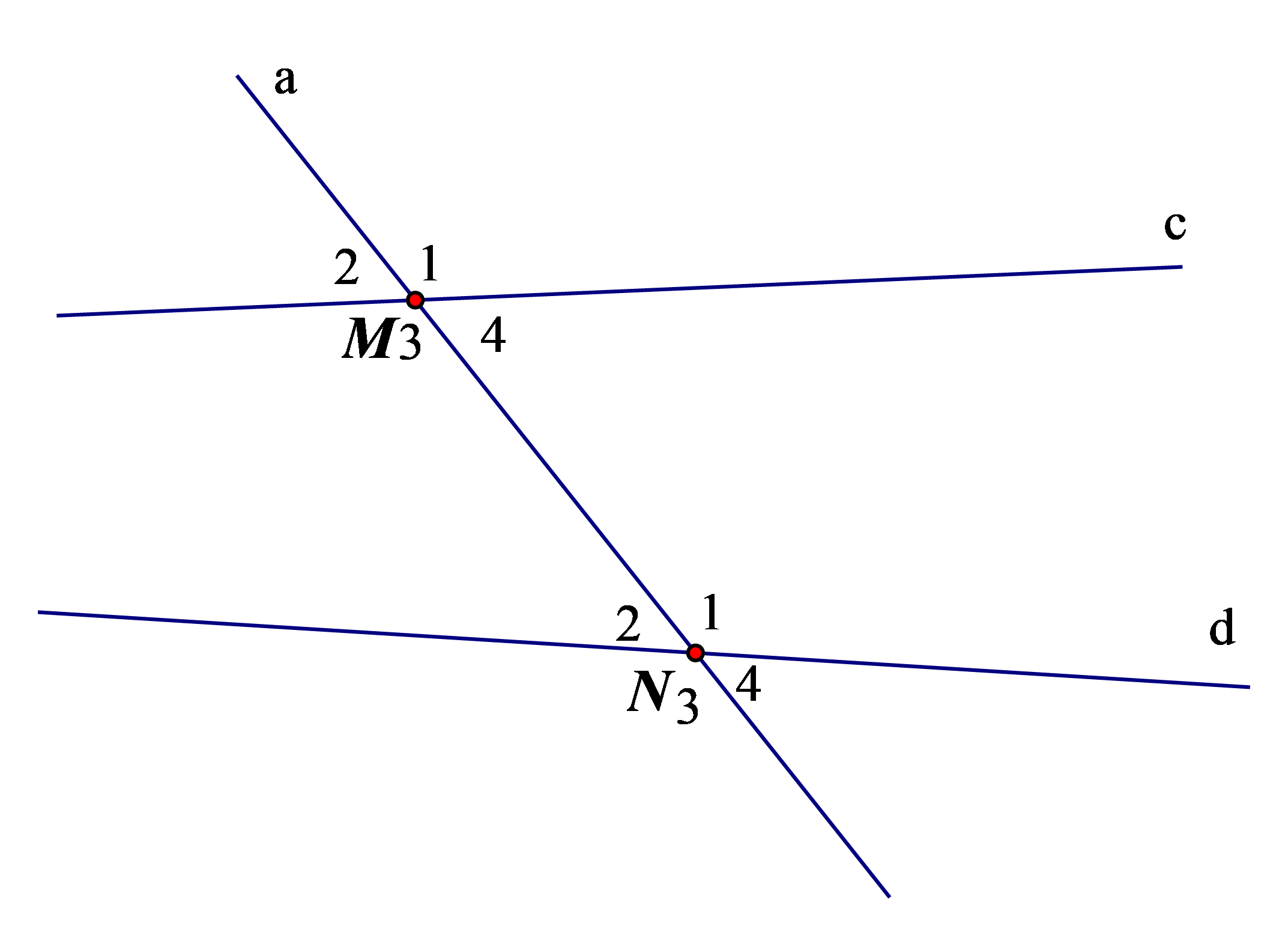 Hướng dẫn giải
Hướng dẫn giải
Các cặp góc so le trong là: M3 và N1; M4 và N2.
Các cặp góc đồng vị là: M1 và N1; M2 và N2; M3 và N3; M4 và N4.
2. Dấu hiệu nhận biết hai đường thẳng song song
- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì a và b song song với nhau.
- Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a và b song song với nhau.
Ví dụ:
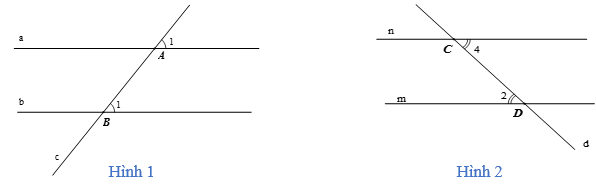
- Ở hình 1: Đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau nên a // b.
- Ở hình 2: Đường thẳng d cắt hai đường thẳng m, n và trong các góc tạo thành có một cặp góc so le trong bằng nhau nên m // n.
Ví dụ: Vẽ một đường thẳng b đi qua điểm M và song song với đường thẳng a (M ∉ a) bằng êke.
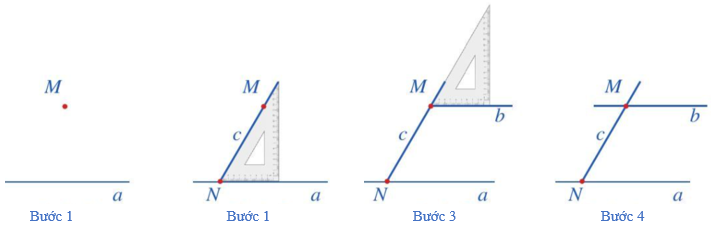 Bước 1: Vẽ đường thẳng a và điểm M không thuộc a.
Bước 1: Vẽ đường thẳng a và điểm M không thuộc a.
Bước 2: Đặt ê ke sao cho cạnh ngắn của góc vuông nằm trên đường thẳng a và cạnh huyền đi qua điểm M, vẽ theo cạnh huyền một phần đường thẳng c đi qua M (đường thẳng c cắt đường thẳng a tại điểm N).
Bước 3: Dịch chuyển ê ke sao cho cạnh huyền của ê ke vẫn nằm trên đường thẳng c còn cạnh ngắn của góc vuông đi qua điểm M, vẽ theo cạnh ngắn của góc vuông một phần đường thẳng b đi qua điểm M.
Bước 4: Vẽ hoàn thiện đường thẳng b.
Nhận xét: Qua một điểm ở ngoài một đường thẳng luôn có một đường thẳng song song với đường thẳng đó.
3. Tiên đề Euclid về đường thẳng song song
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Nhận xét: Nếu hai đường thẳng cùng đi qua điểm M và cùng song song song với đường thẳng a (M ∉ a) thì hai đường thẳng đó trùng nhau.
Ví dụ:
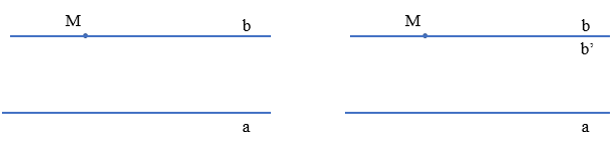 Qua điểm M nằm ngoài đường thẳng a ta vẽ được một đường thẳng b song song với a.
Qua điểm M nằm ngoài đường thẳng a ta vẽ được một đường thẳng b song song với a.
Và vẽ được đường thẳng b’ cũng đi qua M và b’ song song với a.
Khi đó theo Tiên đề Euclid thì b và b’ trùng nhau.
4. Tính chất của hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì:
- Hai góc đồng vị bằng nhau.
- Hai góc so le trong bằng nhau.
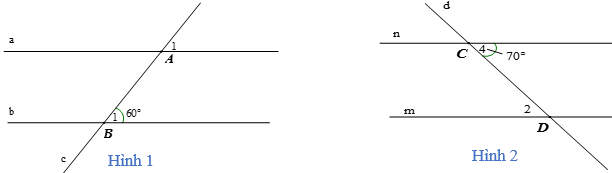
Ví dụ: Tính số đo các góc A1 và góc D2 trong hai hình vẽ sau, biết a // b và m // n.
Hướng dẫn giải
- Hình 1: Do a // b nên ta có: (hai góc đồng vị), mà nên .
Vậy .
- Hình 2: Do m // n nên: (hai góc so le trong), mà nên .
Vậy .
Chú ý: Nếu đường thẳng c cắt hai đường thẳng song song a và b thì:
+ Hai góc so le ngoài bằng nhau.
+ Hai góc trong cùng phía có tổng số đo bằng 180°.
Ví dụ:
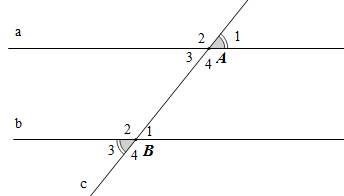
- Các cặp góc so le ngoài A1 và B3; A2 và B4; Khi đó: và .
- Hai góc trong cùng phía: góc A3 và góc B2; góc A4 và góc B1.
Khi đó: ; .