Với giải sách bài tập Toán 7 Bài 1: Biểu thức số, biểu thức đại số sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 1: Biểu thức số, biểu thức đại số

Giải Toán 7 trang 25 Tập 2

Bài 1 trang 25 Toán 7 Tập 2:Hãy viết biểu thức số biểu thị diện tích hình bình hành có độ dài cạnh đáy bằng 6 cm và chiều cao bằng 5 cm.

Lời giải:

Ta đã biết diện tích của hình bình hành bằng tích của độ dài cạnh đáy với chiều cao.

Biểu thức số biểu thị diện tích hình bình hành có độ dài cạnh đáy bằng 6 cm và chiều cao bằng 5 cm là 6 . 5 (cm²).

Vậy biểu thức số biểu thị diện tích hình bình hành đã cho là: 6 . 5 cm².

Bài 2 trang 25 Toán 7 Tập 2:Hãy viết biểu thức số biểu thị số quả cam được xếp trong 4 lớp trên cùng của khối trong Hình 1.

Lời giải:

Dựa vào Hình 1 ta thấy:

+ Số quả cam xếp trong lớp đầu tiên trên cùng là: 1 (quả);

+ Số quả cam xếp trong lớp thứ hai trên cùng là: 2² (quả);

+ Số quả cam xếp trong lớp thứ ba trên cùng là: 3² (quả);

+ Số quả cam xếp trong lớp thứ tư trên cùng là: 4² (quả).

Vậy biểu thức số biểu thị số quả cam được xếp trong 4 lớp trên cùng của khối trong Hình 1 là: 1 + 2² + 3² + 4².

Bài 3 trang 25 Toán 7 Tập 2:Hãy viết biểu thức đại số biểu thị diện tích của một hình thoi có đường chéo thứ nhất dài hơn đường chéo thứ hai 4 cm.

Lời giải:

Gọi a (cm) là độ dài của đường chéo thứ nhất.

Do hình thoi có đường chéo thứ nhất dài hơn đường chéo thứ hai 4 cm nên độ dài đường chéo thứ hai bằng: a – 4 (cm) (a > 4).

Diện tích hình thoi bằng nửa tích độ dài hai đường chéo.

Vậy biểu thức đại số biểu thị diện tích của hình thoi trên là: $\frac{1}{2}$ a.(a – 4) (cm²).

Bài 4 trang 25 Toán 7 Tập 2:Hãy viết biểu thức đại số biểu thị thể tích của một hình hộp chữ nhật có chiều dài hơn chiều rộng 6 cm và hơn chiều cao 3 cm.

Lời giải:

Gọi x (cm) là chiều dài của hình hộp chữ nhật.

Do hình hộp chữ nhật có chiều dài hơn chiều rộng 6 cm nên chiều rộng của hình hộp chữ nhật bằng: x – 6 (cm) (x > 6).

Do hình hộp chữ nhật có chiều dài hơn chiều cao 3 cm nên chiều cao của hình hộp chữ nhật bằng: x – 3 (cm).

Vậy biểu thức đại số biểu thị thể tích của hình hộp chữ nhật đó là:

x(x – 6)(x – 3) (cm³).

Bài 5 trang 25 Toán 7 Tập 2:Hãy viết biểu thức đại số biểu thị:

a) Tổng của 3x² + 1 và 5(y – 2);

b) Tổng các bình phương của a + 2 và b – 1.

Lời giải:

a) Biểu thức đại số biểu thị tổng của 3x² + 1 và 5(y – 2) là:

3x² + 1 + 5(y – 2).

b) Biểu thức đại số biểu thị bình phương của a + 2 là: (a + 2)².

Biểu thức đại số biểu thị bình phương của b – 1 là: (b – 1)².

Biểu thức đại số biểu thị tổng các bình phương của a + 2 và b – 1 là:

(a + 2)² + (b – 1)².

Bài 6 trang 25 Toán 7 Tập 2:Nhiệt độ vào buổi sáng ở một thị trấn là x °C, tới trưa thì tăng thêm y °C, và đến tối thì giảm t °C so với buổi trưa. Hãy viết biểu thức biểu thị nhiệt độ vào buổi tối. Tính nhiệt độ vào buổi tối khi biết x = 25; y = 5; t = 7.

Lời giải:

Nhiệt độ vào buổi sáng ở thị trấn là x °C, tới trưa thì tăng thêm y °C nên nhiệt độ lúc trưa là: x + y (°C).

Đến tối thì nhiệt độ giảm t °C so với buổi trưa nên nhiệt độ buổi tối là:

x + y – t (°C).

Tại x = 25, y = 5, t = 7 thì nhiệt độ buổi tối là: 25 + 5 – 7 = 23 (°C).

Vậy biểu thức biểu thị nhiệt độ vào buổi tối là: x + y – t (°C) và khi x = 25; y = 5; t = 7 thì nhiệt độ vào buổi tối là 23 °C.

Bài 7 trang 25 Toán 7 Tập 2:Rút gọn các biểu thức sau:

a) 4(2y – 3x) – 3(x – 2y);

b) x² + 5y – 2y – 7x².

Lời giải:

a) 4(2y – 3x) – 3(x – 2y)

= 4 . 2y – 4 . 3x – 3 . x – 3 . (–2y)

= 8y – 12x – 3x + 6y

= (8y + 6y) + (– 12x – 3x)

= 14y – 15x.

b) x² + 5y – 2y – 7x²

= (x² – 7x²) + (5y – 2y)

= –6x² + 3y.

Giải Toán 7 trang 26 Tập 2

Bài 8 trang 26 Toán 7 Tập 2:Một mảnh vườn hình chữ nhật có chiều rộng bằng a (m), chiều dài hơn chiều rộng 6 m. Người ta làm lối đi rộng x (m) (xem Hình 2). Hãy viết biểu thức biểu thị diện tích phần còn lại của mảnh vườn. Tính diện tích ấy khi a = 30 m, x = 1 m.

Lời giải:

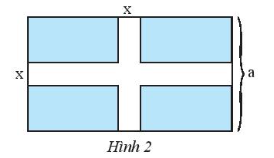
Do mảnh vườn hình chữ nhật có chiều rộng bằng a (m), chiều dài hơn chiều rộng 6 m nên chiều dài mảnh vườn bằng: a + 6 (m).

Diện tích mảnh vườn hình chữ nhật đó là: a . (a + 6) (m²).

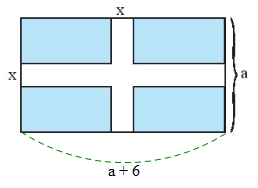
Diện tích của lối đi ngang là: x . (a + 6) (m²).

Diện tích của lối đi dọc là: x . a (m²).

Diện tích phần lối đi ngang và lối đi dọc cùng đi qua là: x . x = x² (m²).

Nhưng do phần lối đi ở giữa mảnh vườn được tính hai lần nên diện tích toàn bộ lối đi là: x(a + 6) + xa – x² (m²).

Diện tích phần còn lại của mảnh vườn là:

a(a + 6) – [x(a + 6) + xa – x²]

= a . a + a . 6 – (x . a + x . 6 + xa – x²)

= a² + 6a – (2xa + 6x – x²)

= a² + 6a – 2xa – 6x + x² (m²).

Khi a = 30 và x = 1 thì diện tích trên bằng:

30² + 6 . 30 – 2 . 1 . 30 – 6 . 1 + 1²

= 900 + 180 – 60 – 6 + 1 = 1 015 (m²).

Vậy biểu thức biểu thị diện tích phần còn lại của mảnh vườn là: a² + 6a – 2xa – 6x + x² (m²).

Diện tích phần còn lại của mảnh vườn khi a = 30 và x = 1 bằng 1 015 m².

Bài 9 trang 26 Toán 7 Tập 2:Mỗi buổi sáng bạn Thu tập đi bộ kết hợp với chạy. Biết vận tốc đi bộ là 4 km/giờ và chạy là 8 km/giờ.

a) Viết biểu thức biểu thị quãng đường mà bạn Thu đã đi bộ x giờ và chạy y giờ.

b) Tính quãng đường khi x = 15 phút và y = 30 phút.

Lời giải:

a) Quãng đường bạn Thu đi bộ trong x giờ là: 4x (km).

Quãng đường bạn Thu chạy trong y giờ là: 8y (km).

Quãng đường mà bạn Thu đã đi bộ x giờ và chạy y giờ là: 4x + 8y (km).

Vậy biểu thức biểu thị quãng đường mà bạn Thu đã đi bộ x giờ và chạy y giờ là: 4x + 8y.

b) Đổi x = 15 phút = $\frac{1}{4}$  giờ và y = 30 phút = $\frac{1}{2}$  giờ.

Thay x = $\frac{1}{4}$  và y = $\frac{1}{2}$  vào biểu thức 4x + 8y ta có:

$4.\frac{1}{4}+8.\frac{1}{2}=1+4=5$ (km).

Vậy quãng đường bạn Thu đã đi bộ 15 phút và chạy 30 phút là 5 km.

Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 6

Bài 1 : Biểu thức số, biểu thức đại số

Bài 2 : Đa thức một biến

Bài 3 : Phép cộng và phép trừ đa thức một biến

Bài 4 : Phép nhân và phép chia đa thức một biến

Lý thuyết Biểu thức số, biểu thức đại số

1. Biểu thức số

- Các số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa tạo thành một biểu thức.

Chẳng hạn: 3 + 7 – 2; 4. 5: 2; 2. (5 + 8) là những biểu thức.

Những biểu thức như trên còn được gọi là biểu thức số.

Ví dụ: Viết biểu thức số biểu thị:

a) Chu vi của hình chữ nhật có chiều dài bằng 6 cm và chiều rộng bằng 4 cm;

b) Diện tích của hình tròn có bán kính bằng 5 cm.

Hướng dẫn giải:

a) Biểu thức số biểu thị chu vi hình chữ nhật: 2.(6 + 4);

b) Biểu thức số biểu thị diện tích hình tròn: π.5².

2. Biểu thức đại số

Biểu thức bao gồm các số và các chữ (đại diện cho số) được nối với nhau bởi các kí hiệu phép toán cộng, trừ, nhân, chia, nâng lên lũy thừa được gọi là biểu thức đại số.

Trong biểu thức đại số:

- Những chữ đại diện cho một số tùy ý gọi là biến số;

- Những chữ đại diện cho một số xác định gọi là hằng số;

Ví dụ: xy – 2. x²y là biểu thức đại số với 2 biến là x và y; 2 là hằng số;

ab + $\frac{b^3}{6}$+ c là biểu thức đại số với ba biến là a, b và c; hằng số là $\frac{1}{6}$.

Chú ý:

- Trong biểu thức đại số, vì biến đại diện cho số nên khi thực hiện các phép tính trên các biến, ta có thể áp dụng những tính chất, quy tắc phép toán như trên các số. Chẳng hạn:

x + y = y + z;

(x + y) + z = x + (y + z);

(xy)z = x(yz);

xy = yx;

xxx = x³;

x(y + z) = xy + xz

Ví dụ: Rút gọn các biểu thức sau:

a)6x + 4x;

b)4(x + 2x) – (x² – 2x)

c)6(y – x) – 2(x – y).

Hướng dẫn giải:

a)6x + 4x = (6 + 4). x = 10x;

b)4(x + 2x) – (x² – 2x)

=4x + 8x – x² + 2x

=4x + 8x + 2x – x²

=14x – x².

c)6(y – x) – 2(x – y)

=6y – 6x – 2x + 2y

=6y + 2y – 6x – 2x

=8y – 8x.

3. Giá trị của biểu thức đại số

Để tính giá trị của một biểu thức đại số ta thực hiện các bước sau:

- Bước 1: Thay chữ bởi giá trị số đã cho (chú ý các trường hợp phải đặt số trong dấu ngoặc);

- Bước 2: Thực hiện các phép tính (chú ý đến thứ tự thực hiện các phép tính: thực hiện phép lũy thừa, rồi đến phép nhân chia, sau đó là phép cộng trừ).

Ví dụ: Tính giá trị của biểu thức a² – 5b + 1 khi a = 4 và b = 2.

Hướng dẫn giải:

Thay a = 4 và b = 2 vào biểu thức trên, ta được:

a² – 5b + 1 = 4² – 5. 2 + 1 = 16 – 10 + 1 = 7.

Vậy khi a = 4 và b = 2 thì giá trị của biểu thức a² – 5b + 1 là 7.