Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 1: Biểu thức số và biểu thức đại số chi tiết sách Toán 7 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 1: Biểu thức số và biểu thức đại số
1. Biểu thức số
Khởi động 1 trang 25 Toán lớp 7: Hai biểu thức và có gì khác nhau?
Phương pháp giải:
Phân biệt biểu thức số và biểu thức đại số.
Lời giải:
Biểu thức là một biểu thức số trong đó các số được nối với nhau bởi các phép tính cộng, nhân, chia, nâng lên lũy thừa.
Biểu thức là biểu thức đại số với hai biến x, y trong đó gồm các số và các chữ x, y được nối với nhau bởi các kí hiệu phép toán cộng, nhân, nâng lên lũy thừa.
Phương pháp giải:
Sử dụng công thức tính chu vi và diện tích hình vuông
Lời giải:
Chu vi hình vuông là: C = 4.3 = 12 (cm)
Diện tích hình vuông là: S = 3.3 = 9 ()
Phương pháp giải:
Dựa vào công thức diện tích hình thoi = . tích 2 đường chéo
Lời giải:
Diện tích hình thoi là: )
2. Biểu thức đại số
Phương pháp giải:
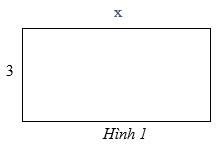
Diện tích hình chữ nhật = chiều dài . chiều rộng
Lời giải:
Diện tích hình chữ nhật là: S = ()
b) Hãy viết biểu thức biểu thị diện tích hình thang có đáy lớn bằng a cm, đáy nhỏ bằng b cm, đường cao bằng h cm.
Phương pháp giải:
• Dựa vào công thức tính thể tích hình lập phương
• Dựa bào công thức tính diện tích hình thang
Lời giải:
a) Thể tích hình lập phương là: V =
b) Diện tích hình thoi = (đáy lớn + đáy nhỏ). chiều cao : 2
Diện tích hình thang là: S =
Phương pháp giải:
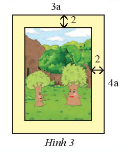
Ta tìm các kích thước của tấm ảnh bằng những chỉ số đã cho
Lời giải:
Chiều dài bức ảnh là :
Chiều rộng bức ảnh là :
Diện tích bức ảnh là: ()
3. Giá trị của biểu thức đại số
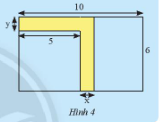
a) Hãy viết biểu thức biểu thị diện tích phần còn lại của khu vườn.
b) Tính diện tích phần còn lại của khu vườn khi x = 1m và y = 0,8m
Phương pháp giải:
Lời giải:
a) Diện tích mảnh vườn còn lại = diện tích mảnh bên trái + diện tích mảnh bên phải :
Diện tích mảnh vườn còn lại bên trái là : 5 . ( 6 – y )
Diện tích mảnh vườn còn lại bên phải là : 6 . ( 10 – 5 – x )
Diện tích mảnh vườn còn lại là : 30 -5y + 30 – 6x = 60 – 6x – 5y ()
b) Thay x = 1 và y = 0,8 vào biểu thức vừa tìm được ở câu a ta có :
60 – 6.1 – 5.0,8 = 50 ()
Thực hành 3 trang 27 Toán lớp 7: Hãy tính giá trị của biểu thức khi x = 2
Phương pháp giải:
Thay x = 2 vào biểu thức đã cho
Lời giải:
Thay x = 2 vào biểu thức đã cho, ta có :
Tính giá bán của đôi giày khi C = 600 nghìn đồng và r = 10%
Phương pháp giải:
Lời giải:
Vì thuế giá trị gia tăng là 10% nên số tiền thuế sẽ là : 10%.600 = 60 (nghìn đồng)
Vậy giá trị của đôi giày khi bán là : 600 + 60 = 660 (nghìn đồng)
Bài tập (trang 28)
Phương pháp giải:
Dựa vào công thức tính diện tích xung quanh hình hộp chữ nhật:
Diện tích xung quanh hình hộp chữ nhật = 2 . chiều cao . ( chiều dài + chiều rộng)
Lời giải:
Biểu thức số biểu thị diện tích xung quanh của hình hộp chữ nhật là: S = 2.2.(7+4)
Phương pháp giải:
Chu vi hình chữ nhật = 2.(Chiều dài + chiều rộng)
Lời giải:
Gọi chiều dài của hình chữ nhật là x ( cm)
Chiều rộng hình chữ nhật là x – 7 (cm) (vì chiều dài hơn chiều rộng 7 cm)
Vậy chu vi hình chữ nhật là:
Phương pháp giải:
Thể tích của hình hộp chữ nhật = chiều dài . chiều rộng . chiều cao
Lời giải:
Gọi chiều dài hình hộp chữ nhật là x (cm)
Chiều rộng của hình hộp chữ nhật là: x – 4 (cm) (do chiều dài hơn chiều rộng 4 cm)
Chiều cao của hình hộp chữ nhật là: x - 2 (cm) (do chiều dài hơn chiều cao 2 cm)
Thể tích hình hộp chữ nhật là:
Bài 4 trang 28 Toán lớp 7: Hãy viết biểu thức đại số biểu thị:
a) Tổng của và
b) Tổng các bình phương của a và b
Phương pháp giải:
Mô tả các phép tính
Lời giải:
a) Tổng của và là:
b) Tổng các bình phương của a và b là:
Phương pháp giải:
Lập biểu thức và thay số
Lời giải:
Số tiền sau khi Lân tiêu y nghìn đồng là : x – y (nghìn đồng)
Sau khi chị Mai cho thêm z nghìn đồng số tiền Lân có là : x – y + z ( nghìn đồng)
Số tiền Lân có là: 100 – 60 + 50 = 90 (nghìn đồng)
Bài 6 trang 28 Toán lớp 7: Rút gọn các biểu thức đại số sau:
a)
b)
Phương pháp giải:
Sử dụng tính chất giao hoán và tính chất phân phối của phép nhân đối với phép cộng.
Lời giải:
a) Cách 1:
Cách 2:
b)
Phương pháp giải:
Lời giải:
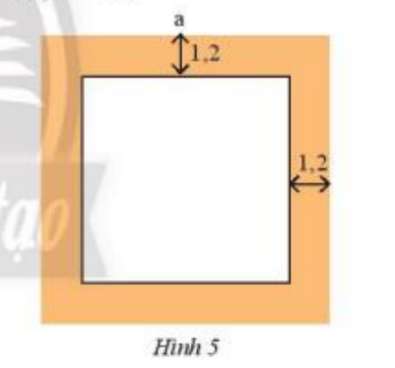
1 cạnh của mảnh vườn còn lại là : a – 1,2 – 1,2 = a – 2,4 (m)
Diện tích mảnh vườn còn lại có biểu thức tính là : ()
Thay a = 20 vào biểu thức ta vừa tính được :
)
Phương pháp giải:
Áp dụng công thức và những số liệu đề bài đã cho để tìm kết quả
Lời giải:
Ta có công thức tính lương là :
Ta thay C = 5 và n = 5 vào công thức, ta có : (triệu đồng)
Vậy lương trung bình của công nhân năm 2020 là 6,08 triệu đồng.
Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:
Bài 3: Phép cộng và phép trừ đa thức một biến
Bài 4: Phép nhân và phép chia đa thức một biến
1. Biểu thức số
- Các số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa tạo thành một biểu thức.
Chẳng hạn: 3 + 7 – 2; 4. 5: 2; 2. (5 + 8) là những biểu thức.
Những biểu thức như trên còn được gọi là biểu thức số.
Ví dụ: Viết biểu thức số biểu thị:
a) Chu vi của hình chữ nhật có chiều dài bằng 6 cm và chiều rộng bằng 4 cm;
b) Diện tích của hình tròn có bán kính bằng 5 cm.
Hướng dẫn giải:
a) Biểu thức số biểu thị chu vi hình chữ nhật: 2.(6 + 4);
b) Biểu thức số biểu thị diện tích hình tròn: π.52.
2. Biểu thức đại số
Biểu thức bao gồm các số và các chữ (đại diện cho số) được nối với nhau bởi các kí hiệu phép toán cộng, trừ, nhân, chia, nâng lên lũy thừa được gọi là biểu thức đại số.
Trong biểu thức đại số:
- Những chữ đại diện cho một số tùy ý gọi là biến số;
- Những chữ đại diện cho một số xác định gọi là hằng số;
Ví dụ: xy – 2. x2y là biểu thức đại số với 2 biến là x và y; 2 là hằng số;
ab + + c là biểu thức đại số với ba biến là a, b và c; hằng số là .
Chú ý:
- Trong biểu thức đại số, vì biến đại diện cho số nên khi thực hiện các phép tính trên các biến, ta có thể áp dụng những tính chất, quy tắc phép toán như trên các số. Chẳng hạn:
x + y = y + z;
(x + y) + z = x + (y + z);
(xy)z = x(yz);
xy = yx;
xxx = x3;
x(y + z) = xy + xz
Ví dụ: Rút gọn các biểu thức sau:
a)6x + 4x;
b)4(x + 2x) – (x2 – 2x)
c)6(y – x) – 2(x – y).
Hướng dẫn giải:
a)6x + 4x = (6 + 4). x = 10x;
b)4(x + 2x) – (x2 – 2x)
=4x + 8x – x2 + 2x
=4x + 8x + 2x – x2
=14x – x2.
c)6(y – x) – 2(x – y)
=6y – 6x – 2x + 2y
=6y + 2y – 6x – 2x
=8y – 8x.
3. Giá trị của biểu thức đại số
Để tính giá trị của một biểu thức đại số ta thực hiện các bước sau:
- Bước 1: Thay chữ bởi giá trị số đã cho (chú ý các trường hợp phải đặt số trong dấu ngoặc);
- Bước 2: Thực hiện các phép tính (chú ý đến thứ tự thực hiện các phép tính: thực hiện phép lũy thừa, rồi đến phép nhân chia, sau đó là phép cộng trừ).
Ví dụ: Tính giá trị của biểu thức a2 – 5b + 1 khi a = 4 và b = 2.
Hướng dẫn giải:
Thay a = 4 và b = 2 vào biểu thức trên, ta được:
a2 – 5b + 1 = 42 – 5. 2 + 1 = 16 – 10 + 1 = 7.
Vậy khi a = 4 và b = 2 thì giá trị của biểu thức a2 – 5b + 1 là 7.