Với giải sách bài tập Toán 7 Bài tập cuối chương 6 sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài tập cuối chương 6

Giải Toán 7 trang 17 Toán 7 Tập 2

Bài 1 trang 17 Toán 7 Tập 2: Tìm a, b, c biết:

a) $\frac{a}{2}=\frac{b}{1}=\frac{c}{3}$  và a + b + c = 48.

b) $\frac{a}{2}=\frac{b}{3};\frac{b}{2}=\frac{c}{3}$  và a + c = 26.

Lời giải:

a) Từ $\frac{a}{2}=\frac{b}{1}=\frac{c}{3}$  và a + b + c = 48, áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{a}{2}=\frac{b}{1}=\frac{c}{3}=\frac{a+b+c}{2+1+3}=\frac{48}{6}=8.$

Khi đó:

• $\frac{a}{2}$  = 8 nên x = 8 . 2 = 16;

• $\frac{b}{1}$  = 8 nên y = 8 . 1 = 8;

• $\frac{c}{3}$  = 8 nên c = 8 . 3 = 24.

Vậy a = 16, b = 8, c = 24.

b) Ta có: $\frac{a}{2}=\frac{b}{3}$  suy ra $\frac{a}{2}:2=\frac{b}{3}:2$  hay $\frac{a}{2}.\frac{1}{2}=\frac{b}{3}.\frac{1}{2}$  tức là $\frac{a}{4}=\frac{b}{6}.$

               $\frac{b}{2}=\frac{c}{3}$  suy ra $\frac{b}{2}:3=\frac{c}{3}:3$  hay $\frac{b}{2}.\frac{1}{3}=\frac{c}{3}.\frac{1}{3}$  tức là $\frac{b}{6}=\frac{c}{9}.$

Khi đó $\frac{a}{4}=\frac{b}{6}=\frac{c}{9}$ .

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{a}{4}=\frac{b}{6}=\frac{c}{9}=\frac{a+c}{4+9}=\frac{26}{13}=2$.

Khi đó:

• $\frac{a}{4}=2$  nên x = 2 . 4 = 8;

• $\frac{b}{6}=2$  nên y = 2 . 6 = 12;

• $\frac{c}{9}=2$  nên c = 2 . 9 = 18.

Vậy a = 8, b = 12, c = 18.

Bài 2 trang 17 Toán 7 Tập 2: Dựa theo bảng giá trị tương ứng trong mỗi trường hợp sau, hãy cho biết hai đại lượng có tỉ lệ nghịch với nhau hay không.

a)

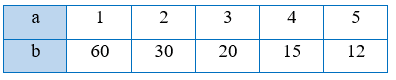
b)

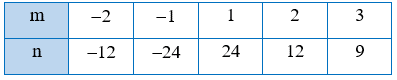
Lời giải:

a) Ta có:

Với a = 1 và b = 60 thì a . b = 1 . 60 = 60;

Với a = 2 và b = 30 thì a . b = 2 . 30 = 60;

Với a = 3 và b = 20 thì a . b = 3 . 20 = 60;

Với a = 4 và b = 15 thì a . b = 4 . 15 = 60;

Với a = 5 và b = 12 thì a . b = 5 . 12 = 60.

Khi đó 1 . 60 = 2 . 30 = 3 . 20 = 4 . 15 = 5 . 12 (vì cùng bằng 60).

Vậy a và b tỉ lệ nghịch với nhau.

b) Ta có:

Với m = -2 và n = -12 thì m . n = (-2) . (-12) = 24;

Với m = -1 và n = -24 thì m . n = (-1) . (-24) = 24;

Với m = 1 và n = 24 thì m . n = 1 . 24 = 24;

Với m = 2 và n = 12 thì m . n = 2 . 12 = 24;

Với m= 3 và n = 9 thì m . n = 3 . 9 = 27.

Khi đó (-2) . (-12) = (-1) . (-24) = 1 . 24 = 2 . 12 ≠ 3 . 9

Vậy a và b không tỉ lệ nghịch với  nhau.

Giải Toán 7 trang 18 Tập 2

Bài 3 trang 18 Toán 7 Tập 2: Thay số thích hợp vào dấu ? trong bảng sau sao cho hai đại lượng x và y tỉ lệ nghịch với nhau

Lời giải:

Để x và y tỉ lệ nghịch với nhau thì xy = (-5) . 8 = -40.

Suy ra x = $\frac{-40}{y}$  và y = $\frac{-40}{x}.$

Khi đó:

• Với x = 5 thì $y=\frac{-40}{5}=-8;$

• Với y = -12 thì $x=\frac{-40}{-12}=\frac{10}{3};$

• Với x = 3 thì $y=\frac{-40}{3}=-\frac{40}{3};$

• Với x = 2 thì $y=\frac{-40}{2}=-20;$

• Với x = -4 thì $y=\frac{-40}{-4}=10.$

Vậy ta có bảng sau:

Bài 4 trang 18 Toán 7 Tập 2:

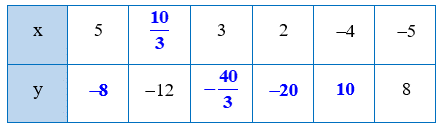
a) Tìm ba số x, y, z thỏa mãn x : y : z = 1 : 2 : 2 và x + y + z = 25.

b) Tìm ba số a, b, c thỏa mãn a : b : c = 3 : 4 : 5 và a + b – c = 100.

Lời giải:

a) Từ x : y : z = 1 : 2 : 2 ta có $\frac{x}{1}=\frac{y}{2}=\frac{z}{2}$ .

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{1}=\frac{y}{2}=\frac{z}{2}=\frac{x+y+z}{1+2+2}=\frac{25}{5}=5$.

Khi đó:

• $\frac{x}{1}=5$  nên x = 5 . 1 = 5;

• $\frac{y}{2}=5$  nên y = 5 . 2 = 10;

• $\frac{z}{2}=5$  nên y = 5 . 2 = 10.

Vậy x = 5, y = 10, z = 10.

b) Từ a : b : c = 3 : 4 : 5 ta có $\frac{a}{3}=\frac{b}{4}=\frac{c}{5}$ .

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b-c}{3+4-5}=\frac{100}{2}=50.$

Khi đó:

• $\frac{a}{3}=50$  nên a = 50 . 3 = 150;

• $\frac{b}{4}=50$  nên b = 50 . 4 = 200;

• $\frac{c}{5}=50$  nên c = 50 . 5 = 250.

Vậy a = 150; b = 200; c = 250.

Bài 5 trang 18 Toán 7 Tập 2: Một nông trường có 4 máy gặt (cùng năng suất) đã gặt xong một cánh đồng hết 6 giờ. Hỏi nếu có 6 máy gặt như thế sẽ gặt xong cánh đồng đó hết bao nhiêu thời gian?

Lời giải:

Gọi x (giờ) là thời gian 6 máy gặt sẽ gặt xong cánh đồng đó.

Do số máy gặt và thời gian gặt xong một cánh đồng là hai đại lượng tỉ lệ nghịch nên áp dụng tính chất của các đại lượng tỉ lệ nghịch ta có:

6x = 4 . 6 = 24 suy ra $x=\frac{24}{6}=4.$

Vậy nếu có 6 máy gặt như thế sẽ gặt xong cánh đồng đó hết 4 giờ.

Bài 6 trang 18 Toán 7 Tập 2: Bạn Cúc muốn cắt một hình chữ nhật có diện tích 100 cm². Gọi d (cm) và r (cm) là hai kích thước của hình chữ nhật. Em hãy viết công thức thể hiện mối quan hệ giữa hai đại lượng d và r.

Lời giải:

Diện tích của hình chữ nhật có hai kích thước là d (cm) và r (cm) là dr (cm²).

Mà diện tích của hình chữ nhật bạn Cúc muốn cắt có diện tích 100 cm² nên dr = 100.

Vậy công thức thể hiện mối quan hệ giữa hai đại lượng d và r là: dr = 100.

Bài 7 trang 18 Toán 7 Tập 2: Cho biết a tỉ lệ thuận với b theo hệ số tỉ lệ m và b tỉ lệ thuận với c theo hệ số tỉ lệ n.

a) Hãy tính a theo b, tính b theo c.

b) Hãy tính a theo c.

Lời giải:

a) Do a tỉ lệ thuận với b theo hệ số tỉ lệ m nên ta có: a = mb.

Do b tỉ lệ thuận với c theo hệ số tỉ lệ n nên ta có: b = nc.

Vậy a = mb và b = nc.

b) Thay b = nc vào a = mb ta có: a = mnc.

Vậy a = mnc.

Bài 8 trang 18 Toán 7 Tập 2: Lớp 7A có 4 bạn làm vệ sinh xong lớp học hết 2 giờ. Hỏi nếu có 16 bạn sẽ làm vệ sinh xong lớp học trong bao lâu? (Biết rằng các bạn có năng suất làm việc như nhau).

Lời giải:

Gọi x (giờ) là thời gian 16 bạn sẽ làm vệ sinh xong lớp học.

Do số bạn làm vệ sinh lớp học và thời gian làm xong là hai đại lượng tỉ lệ nghịch nên áp dụng tính chất của các đại lượng tỉ lệ nghịch ta có:

16x = 4 . 2 = 8 suy ra $x=\frac{8}{16}=\mathrm{0,5}$  giờ = 30 phút.

Vậy nếu có 16 bạn sẽ làm vệ sinh xong lớp học hết 30 phút.

Bài 9 trang 18 Toán 7 Tập 2: Hoa muốn chia đều 1 kg đường vào n túi. Gọi p (g) là lượng đường trong mỗi túi. Hãy chứng tỏ n, p là hai đại lượng tỉ lệ nghịch và tính p theo n.

Lời giải:

Đổi 1 kg = 1 000 g.

Bạn Hoa chia đều 1 kilogam đường (1 000 g đường) vào n túi nên khối lượng đường trong mỗi túi là: $\frac{1000}{n}$  (g).

Mà theo bài p (g) là khối lượng đường trong mỗi túi.

Do đó p = $\frac{1000}{n}$ .

Khi đó, n và p là hai đại lượng tỉ lệ nghịch với nhau theo hệ số tỉ lệ là 1 000.

Vậy công thức tính p theo n là p = $\frac{1000}{n}$

Bài 10 trang 18 Toán 7 Tập 2: Lớp 7C có 2 bạn dọn xong cỏ vườn trường trong 3 giờ. Hỏi nếu có 6 bạn sẽ dọn xong cỏ vườn trường trong bao lâu? (Biết rằng các bạn có năng suất làm việc như nhau.)

Lời giải:

Gọi x (giờ) là thời gian 6 bạn sẽ dọn xong cỏ trong vườn trường.

Do số bạn dọn cỏ và thời gian các bạn dọn xong cỏ trong vườn là hai đại lượng tỉ lệ nghịch nên áp dụng tính chất của các đại lượng tỉ lệ nghịch ta có:

6x = 2 . 3 = 6 suy ra $x=\frac{6}{6}=1.$

Vậy nếu có 6 bạn sẽ dọn xong cỏ vườn trường trong 1 giờ.

Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 3 : Đại lượng tỉ lệ nghịch

Bài tập cuối chương 6

Bài 1 : Biểu thức số, biểu thức đại số

Bài 2 : Đa thức một biến

Bài 3 : Phép cộng và phép trừ đa thức một biến

Tổng hợp lý thuyết Toán 7 Chương 6

1. Tỉ lệ thức:

1.1. Khái niệm:

Với b, c ≠ 0 ta có tỉ lệ thức là đẳng thức của hai tỉ số: $\frac{a}{b}=\frac{c}{d}$

Tỉ lệ thức còn được viết là: a : b = c : d

1.2. Các tính chất:

* Tính chất 1: Nếu $\frac{a}{b}=\frac{c}{d}$ thì ad = bc. (b.d ≠ 0)

* Tính chất 2: Ngược lại so với tính chất 1 ta có:

Nếu ad = bc và a, b, c, d ≠ 0 thì ta có những tỉ lệ thức sau:

$\frac{a}{b}=\frac{c}{d}$; $\frac{a}{c}=\frac{b}{d}$; $\frac{d}{c}=\frac{b}{d}$ ; $\frac{d}{b}=\frac{c}{a}$ .

Ví dụ:Cho đẳng thức x.2 = 3.y.Với x, y ≠ 0 ta có các tỉ lệ thức sau:

$\frac{x}{3}=\frac{y}{2}$; $\frac{2}{3}=\frac{y}{x}$ ; $\frac{x}{y}=\frac{3}{2}$ ; $\frac{2}{y}=\frac{3}{x}$ .

2. Dãy tỉ số bằng nhau:

2.1. Khái niệm:

- Ta gọi các đẳng thức: $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}$ là một dãy các tỉ số bằng nhau.

- Khi có dãy tỉ số bằng nhau $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}$ , ta nói các số a, c, e tỉ lệ với các số b, d, f và có thể ghi là: a : c : e = b : d : f.

2.2. Các tính chất:

* Tính chất 1: $\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}=\frac{a-c}{b-d}$(các mẫu số phải khác 0).

* Tính chất 2: Tương tự với tỉ lệ thức, ta có tính chất sau của dãy tỉ số bằng nhau.

Từ dãy tỉ số bằng nhau $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}$ ta viết được:

$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{a+c+e}{b+d+f}=\frac{a-c+e}{b-d+f}$ (các mẫu số phải khác 0).

3. Khái niệm hai đại lượng tỉ lệ thuận:

Cho k là hằng số khác 0, ta nói đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k nếu y liên hệ với x theo công thức: y = kx.

Từ y = kx (k ≠ 0) ta suy ra $x=\frac{1}{k}y$ . Vậy nếu y tỉ lệ thuận với x theo hệ số tỉ lệ k thì x cũng tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{k}$ và ta nói hai đại lưỡng x, y tỉ lệ thuận với nhau.

4. Tính chất của các đại lượng tỉ lệ thuận:

Nếu hai đại lượng tỉ lệ thuận với nhau thì:

- Tỉ số hai giá trị tương ứng của chúng luôn không đổi:

$\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_3}{x_3}=\mathrm{...}$

- Tỉ số hai giá trị tùy ý của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia:

$\frac{x_1}{x_2}=\frac{y_1}{y_2}$; $\frac{x_1}{x_3}=\frac{y_1}{y_3}$ ;...

5. Khái niệm hai đại lượng tỉ lệ nghịch:

Cho a là một hằng số khác 0. Nếu đại lượng y liên hệ với đại lượng x theo công thức $y=\frac{a}{x}$ hay xy = a thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.

Chú ý: Khi y tỉ lệ nghịch với x thì x cũng tỉ lệ nghịch với y và ta nói hai đại lượng đó tỉ lệ nghịch với nhau.

6. Tính chất của các đại lượng tỉ lệ nghịch:

Nếu hai đại lượng y và x tỉ lệ nghịch với nhau thì:

- Tích hai giá trị tương ứng của chúng luôn không đổi (bằng hệ số tỉ lệ):

x₁y₁ = x₂y₂ = x₃y₃ = … hay $\frac{x_1}{\frac{1}{y_1}}=\frac{x_2}{\frac{1}{y_2}}=\frac{x_3}{\frac{1}{y_3}}=\mathrm{...}$

- Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia:

$\frac{x_1}{x_2}=\frac{x_2}{y_1}$; $\frac{x_1}{x_3}=\frac{y_3}{y_1}$ ; …