Tailieumoi.vn xin giới thiệu Giải bài tập Toán 9 Bài 10: Diện tích hình tròn, hình quạt tròn hay, chi tiết giúp học sinh dễ dàng làm bài tập Diện tích hình tròn, hình quạt tròn lớp 9.

Giải bài tập Toán lớp 9 Bài 10: Diện tích hình tròn, hình quạt tròn

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 97 SGK Toán lớp 9 Tập 2: Hãy điền biểu thức thích hợp vào các chỗ trống (…) trong dãy lập luận sau:

Hình tròn bán kính R (ứng với cung ${360}^0$) có diện tích là …  .

Vậy hình quạt tròn bán kính R, cung $1^0$ có diện tích là … .

Hình quạt tròn bán kính R, cung $n^0$ có diện tích S = … .

Lời giải:

Hình tròn bán kính R (ứng với cung ${360}^0$) có diện tích là $\pi R^2$.

Vậy hình quạt tròn bán kính R, cung $1^0$ có diện tích là  $\frac{\pi R^{2}n}{360}$.

Hình quạt tròn bán kính R, cung $n^0$ có diện tích S = $\frac{\pi R^{2}n}{360}$.

Bài tập (trang 98; 99)

Bài 77 trang 98 SGK Toán lớp 9 Tập 2:Tính diện tích hình tròn nội tiếp một hình vuông có cạnh là 4cm.

Lời giải:

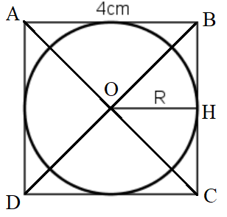
Gọi O là giao điểm hai đường chéo của hình vuông ABCD

Kẻ OH vuông góc với BC tại H

Xét tam giác OBC có:

OB = OC (tính chất hình vuông)

Do đó, tam giác OBC cân tại O

OH vuông góc với BC tại H

Nên OH vừa là đường cao vừa là đường trung tuyến

Do đó, H là trung điểm của BC

Xét tam giác DBC có:

O là trung điểm của BD (tính chất hình vuông)

H là trung điểm của BC  (chứng minh trên)

Do đó, OH là đường trung bình của tam giác DBC

$\Rightarrow OH=\frac{DC}{2}=\frac{4}{2}=2 \left(cm\right)$

Hình tròn nội tiếp hình vuông ABCD có tâm O và bán kính R = OH = 2cm

Diện tích hình tròn là: $S=\pi .R^2=\pi {.2}^2=4\pi \left(c{m}^2\right)$

Bài 78 trang 98 SGK Toán lớp 9 Tập 2:Chân một đồng cát đổ trên một nền phẳng nằm ngang là một hình tròn có chu vi 12m. Hỏi chân đống cát đó chiếm một diện tích là bao nhiêu mét vuông ?

Lời giải:

Chu vi hình tròn là 12m nên ta có: $C=2\pi R=12\Rightarrow R=\frac{12}{2\pi }=\frac{6}{\pi }$ (cm) (với R là bán kính đường tròn)

Diện tích hình tròn là:

$$\begin{gathered} S=\pi R^2=\pi {\left(\frac{6}{\pi }\right)}^2 \\ =\pi .\frac{36}{{\pi }^2}=\frac{36}{\pi }\approx 11,5\left(m^2\right) \end{gathered}$$

Bài 80 trang 98 SGK Toán lớp 9 Tập 2:Một vườn cỏ hình chữ nhật ABCD có AB = 40m, AD = 30m. Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc:

- Mỗi dây thừng dài 20m.

- Một dây thừng dài 30m và dây thừng kia dài 10m.

Hỏi với cách buộc nào thì diện tích cỏ mà cả hai con dê có thể ăn được sẽ lớn hơn (h.60) ?

Lời giải

Theo cách buộc thứ nhất thì diện tích cỏ dành cho mỗi con dê là bằng nhau.

Mỗi diện tích cỏ dành cho mỗi con dê là $\frac{1}{4}$ hình tròn bán kính 20m

$\Rightarrow S=\frac{1}{4}.\pi {.20}^2=100\pi \left(m^2\right)$

Vậy cả hai diện tích là: $2.S=2.100\pi =200\pi \left(m^2\right)$ (1)

Theo cách buộc thứ hai:

Diện tích cỏ dành cho con dê buộc ở A là $\frac{1}{4}$ hình tròn bán kính 30m: $S_1=\frac{1}{4}.\pi {.30}^2=225\pi \left(m^2\right)$

Diện tích cỏ dành cho con dê buộc ở B là $\frac{1}{4}$ hình tròn bán kính 10m:

$S_2=\frac{1}{4}.\pi {.10}^2=25\pi \left(m^2\right)$

Diện tích cỏ dành cho hai con dê là:

$S_1+S_2=$$225\pi +25\pi =250\pi \left(m^2\right)$ (2)

Từ (1) và (2) ta suy ra cách buộc thứ hai sẽ có diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn.

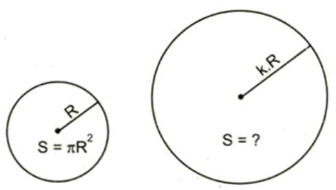
Bài 81 trang 99 SGK Toán lớp 9 Tập 2:Diện tích hình tròn sẽ thay đổi thế nào nếu:

a) Bán kính tăng gấp đôi?

b) Bán kính tăng gấp ba?

c) Bán kính tăng k lần (k > 1)?

Lời giải:

Gọi $S=\pi R^2$ là diện tích hình tròn lúc đầu

a)

Khi bán kính tăng gấp đôi:

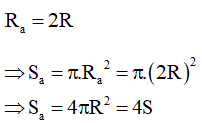
Vậy khi bán kính tăng lên gấp đôi thì diện tích đường tròn tăng lên gấp 4.

b)

Khi bán kính tăng gấp ba:

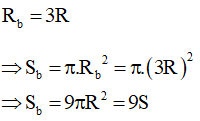
Vậy khi bán kính tăng lên gấp đôi thì diện tích đường tròn tăng lên gấp 9.

c)

Khi bán kính tăng gấp k lần (k > 1):

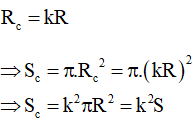
Vậy khi bán kính tăng lên gấp đôi thì diện tích đường tròn tăng lên gấp $k^2$ lần.

Bài 82 trang 99 SGK Toán lớp 9 Tập 2:Điền vào ô trống trong bảng sau (làm tròn kết quả đến chữ số thập phân thứ nhất):

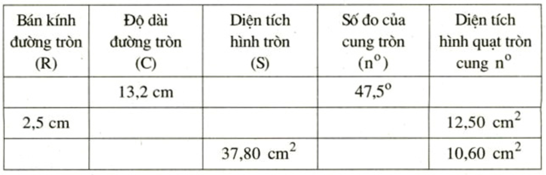
Lời giải:

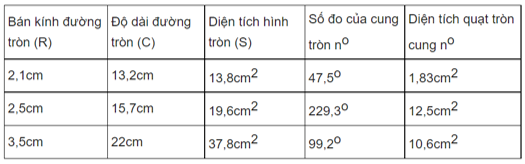
Luyện tập trang 99, 100

Bài 83 trang 99 SGK Toán lớp 9 Tập 2: a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = BI = 2cm. Nêu cách vẽ.

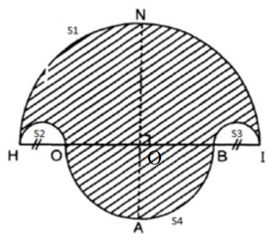
b) Tính diện tích hình HOABINH (miền gạch sọc).

c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó.

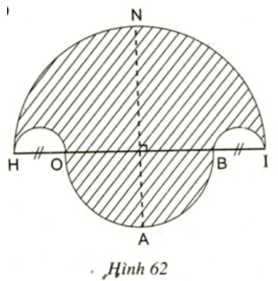
Lời giải:

a)

Cách vẽ

- Vẽ nửa đường tròn đường kính HI = 10cm, tâm M.

- Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.

- Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).

- Vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đường tròn đường kính OB tại A.

b)

$S_1$ là diện tích của nửa đường tròn đường kính HI nên ta có:

$$\begin{gathered} S_1=\frac{1}{2}\pi {\left(\frac{HI}{2}\right)}^2=\frac{1}{2}\pi {\left(\frac{10}{2}\right)}^2 \\ =12,5\pi \left(c{m}^2\right) \end{gathered}$$

$S_2, S_3$ là diện tích của nửa đường tròn đường kính HO và BI với HO = BI = 2cm nên ta có:

$$\begin{gathered} S_2=S_3=\frac{1}{2}\pi {\left(\frac{HO}{2}\right)}^2 \\ =\frac{1}{2}\pi {\left(\frac{2}{2}\right)}^2=0,5\pi \left(c{m}^2\right) \end{gathered}$$

$S_4$ là diện tích của nửa đường tròn đường kính OB nên ta có:

$$\begin{gathered} S_4=\frac{1}{2}\pi {\left(\frac{OB}{2}\right)}^2 \\ =\frac{1}{2}\pi {\left(\frac{HI-OH-BI}{2}\right)}^2 \\ =\frac{1}{2}\pi {\left(\frac{10-2-2}{2}\right)}^2=4,5\pi \left(c{m}^2\right) \end{gathered}$$

Diện tích miền gạch sọc là:

$$\begin{gathered} S=S_1-\left(S_2+S_3\right)+S_4 \\ =12,5\pi -(0,5\pi +0,5\pi )+4,5\pi \\ =16\pi \left(c{m}^2\right) \end{gathered}$$

c)

Điểm N thuộc hình tròn có diện tích $S_1$

Điểm A thuộc hình tròn có diện tích $S_4$

Ta có:  

$$\begin{gathered} NA=ON+OA \\ =\frac{HI}{2}+\frac{OB}{2} \\ =\frac{HI}{2}+\frac{HI-BI-HO}{2} \\ =\frac{10}{2}+\frac{10-2-2}{2}=8 \left(cm\right) \end{gathered}$$

Diện tích hình tròn đường kính NA là:

$$\begin{gathered} S\text{'}=\pi .{\left(\frac{NA}{2}\right)}^2 \\ =\pi .{\left(\frac{8}{2}\right)}^2=16\pi \left(c{m}^2\right)=S \end{gathered}$$

Vậy hình tròn đường kính NA có cùng diện tích với hình HOABINH đó.

Bài 84 trang 99 SGK Toán lớp 9 Tập 2: a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1cm. Nêu cách vẽ (h.63).

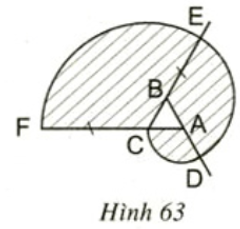
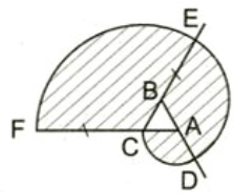
b) Tính diện tích miền gạch sọc.

Lời giải:

a)

Cách vẽ:

- Vẽ tam giác ABC đều cạnh 1cm

- Vẽ $\frac{1}{3}$ đường tròn tâm A, bán kính 1cm, ta được cung CD

- Vẽ $\frac{1}{3}$ đường tròn tâm B, bán kính 2cm, ta được cung DE

- Vẽ $\frac{1}{3}$ đường tròn tâm C, bán kính 3cm, ta được cung EF

Bài 85 trang 100 SGK Toán lớp 9 Tập 2: Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm $\widehat{AOB}={60}^o$ và bán kính đường tròn là 5,1cm (h.64).

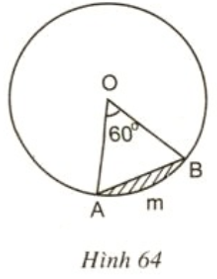
Lời giải

Xét tam giác OAB có:

OA = OB (cùng bằng bán kính R của (O))

Do đó, tam giác OAB cân tại O

Lại có: $\widehat{AOB}={60}^o$ (gt)

Do đó, tam giác OAB là tam giác đều

$\Rightarrow \mathrm{OA}=\mathrm{OB}=\mathrm{AB}=\mathrm{R}=5,1\mathrm{cm}$

Áp dụng công thức diện tích tam giác đều có cạnh a là $\frac{a^2\sqrt{3}}{4}$

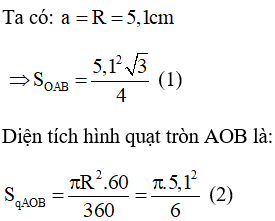
Từ (1) và (2) ta suy ra diện tích hình viên phân là:

$$\begin{gathered} S_{qAOB}-S_{AOB} \\ =\frac{\pi .5,1^2}{6}-\frac{5,1^2\sqrt{3}}{4}\approx 2,4\left(c{m}^2\right) \end{gathered}$$

Bài 86 trang 100 SGK Toán lớp 9 Tập 2: Hình vành khăn là phần hình tròn giữa hai đường tròn đồng tâm (h.65).

a) Tính diện tích S của hình vành khăn theo $R_1$ và $R_2$ (giả sử  $R_1>R_2$ ).

b) Tính diện tích hình vành khăn khi $R_1$ = 10,5cm, $R_2$ = 7,8cm.

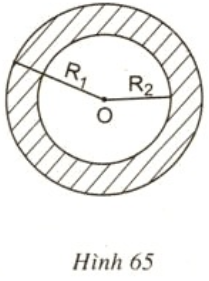
Lời giải:

b)

Thay $R_1$ = 10,5cm, $R_2$ = 7,8cm vào công thức trên ta có diện tích hình vành khăn là:

$$\begin{gathered} S=\pi \left({R_1}^2-{R_2}^2\right) \\ =\pi \left(10,5^2-7,8^2\right)\approx 155,1\left(c{m}^2\right) \end{gathered}$$

Bài 87 trang 100 SGK Toán lớp 9 Tập 2: Lấy cạnh BC của một tam giác đều làm đường kính, vẽ môt nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng BC. Cho biết cạnh BC = a, hãy tính diện tích của hai hình viên phân được tạo thành.

Lời giải:

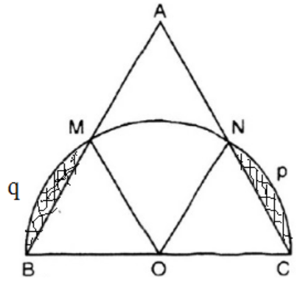
Gọi nửa đường tròn tâm O đường kính BC cắt hai cạnh AB và AC lần lượt tại M và N.

Xét tam giác ONC có:

ON = OC (cùng bằng bán kính đường tròn (O))

Do đó, tam giác ONC là tam giác cân

$\widehat{OCN}={60}^o$ (do tam giác ABC đều)

Do đó, tam giác ONC là tam giác đều

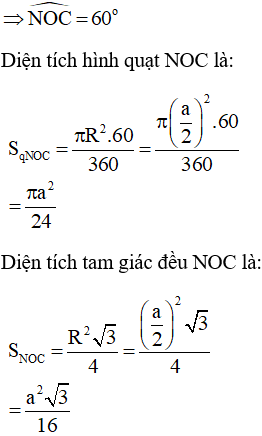
Xét tam giác OMB có:

OM = OB (cùng bằng bán kính đường tròn (O))

Do đó, tam giác OMB là tam giác cân

$\widehat{OBM}={60}^o$ (do tam giác ABC đều)

Do đó, tam giác OMB là tam giác đều

$\Rightarrow \widehat{MOB}={60}^o$

Diện tích 2 hình viên phân được tạo thành là:

$$\begin{gathered} S=S_1+S_2 \\ =\frac{a^2}{48}\left(2\pi -3\sqrt{3}\right)+\frac{a^2}{48}\left(2\pi -3\sqrt{3}\right) \\ =2.\frac{a^2}{48}\left(2\pi -3\sqrt{3}\right) \\ =\frac{a^2}{24}\left(2\pi -3\sqrt{3}\right) \end{gathered}$$