Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 10: Diện tích hình tròn, hình quạt tròn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 10: Diện tích hình tròn, hình quạt tròn
Điền vào ô trống trong bảng sau ( là diện tích hình tròn bán kính ).
|
|
|
|
|
|
|
|
|
Vẽ đồ thị biểu diễn diện tích hình tròn theo bán kính của nó.
Diện tích hình tròn có tỉ lệ thuận với bán kính không?
Phương pháp giải:
Ta sử dụng kiến thức: Độ dài của một đường tròn bán kính được tính theo công thức:
Lời giải:

Vẽ đồ thị:
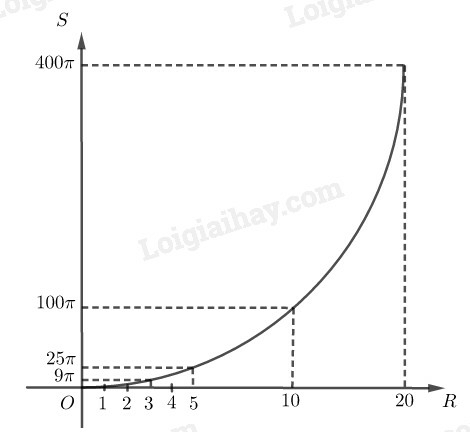
Diện tích hình tròn không tỉ lệ thuận với bán kính
Điền vào ô trống trong bảng sau ( là diện tích hình quạt ).
|
Cung |
|||||
|
|
|
|
|
|
Vẽ đồ thị biểu diễn diện tích hình quạt theo .
Diện tích hình quạt có tỉ lệ thuận với số đo độ của cung không
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích hình quạt tròn bán kính cung được tính theo công thức: hay
Lời giải:
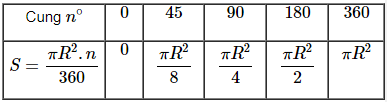
Vẽ đồ thị:
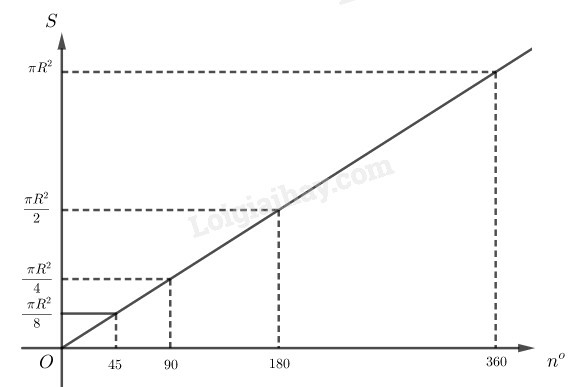
Diện tích hình quạt tròn tỉ lệ thuận với số đo độ của cung tròn.
Ta sử dụng kiến thức:
+) Độ dài của một đường tròn bán kính được tính theo công thức:
+) Diện tích của một hình tròn bán kính được tính theo công thức:
Lời giải:
Gọi bán kính của hình tròn là diện tích là
Ta có:
(đơn vị diện tích)
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích của một hình tròn bán kính được tính theo công thức:
Lời giải:
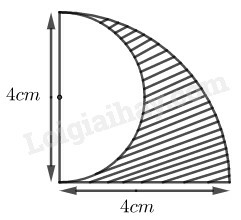
Hình để trắng là nửa hình tròn có đường kính nên bán kính bằng có diện tích:
Diện tích hình tròn có bán kính
Diện tích phần gạch sọc:
Vậy:
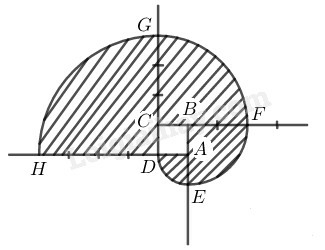
Vẽ đường xoắn xuất phát từ một hình vuông cạnh Nói cách vẽ.
Tính diện tích hình gạch sọc.
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích của một hình tròn bán kính được tính theo công thức:
Lời giải:
- Vẽ hình vuông có cạnh
- Vẽ cung đường tròn tâm bán kính ta được cung
- Vẽ cung đường tròn tâm bán kính ta được cung
- Vẽ cung đường tròn tâm bán kính ta được cung
- Vẽ cung đường tròn tâm bán kính ta được cung
Tính diện tích phần gạch sọc.
Diện tích hình quạt
Diện tích hình quạt
Diện tích hình quạt
Diện tích hình quạt
Diện tích phần gạch sọc:
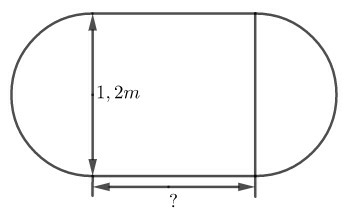
Kích thước kia của hình chữ nhật phải là bao nhiều nếu diện tích mặt bàn tăng gấp đôi sau khi nới
Kích thước kia của hình chữ nhật phải là bao nhiêu nếu chu vi mặt bàn tăng gấp đôi sau khi nới
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích của một hình tròn bán kính được tính theo công thức:
Lời giải:
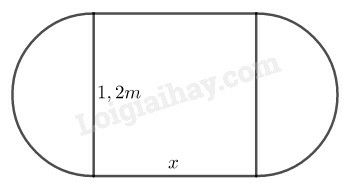
Gọi kích thước thứ của hình chữ nhật là điều kiện:
Ta có:
Gọi kích thước thứ của hình chữ nhật là điều kiện:
Chu vi mặt bàn mới là
Theo bài ra ta có:
Ta sử dụng kiến thức:
+) Áp dụng tính chất dãy tỉ số bằng nhau: Từ dãy tỉ số bằng nhau ta suy ra:
+) Diện tích hình quạt tròn bán kính cung được tính theo công thức: .
Lời giải:
Gọi số đo độ của cung theo thứ tự là
Ta có
Theo bài ra ta có:
Diện tích các hình quạt tương ứng với cung là
Tính diện tích hình quạt tròn (ứng với cung nhỏ )
Tính diện tích hình viên phân (ứng với cung nhỏ )
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích hình quạt tròn bán kính cung được tính theo công thức: .
Lời giải:
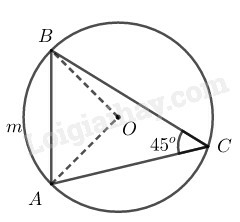
Xét đường tròn có là g
óc nội tiếp chắn
Diện tích hình quạt là:
(đơn vị diện tích)
Diện tích tam giác là:
Diện tích hình viên phân là:
(đơn vị diện tích)
Phương pháp giải:
Ta sử dụng kiến thức:
+) Diện tích hình quạt tròn bán kính cung được tính theo công thức: .
Lời giải:
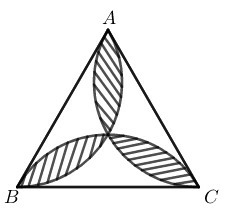
Diện tích hình hoa thị bằng tổng diện tích hình viên phân trừ diện tích tam giác đều
Gọi là tâm của tam giác đều
Vì đều nên là phân giác của các góc
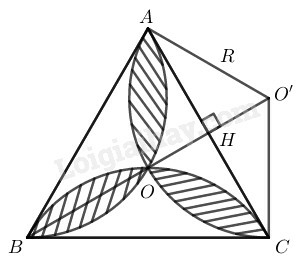
Trong tam giác có ,
(đơn vị diện tích)
có ;
(đơn vị diện tích)
Diện tích hình viên phân:
Diện tích tam giác đều cạnh (đơn vị diện tích)
Diện tích hình hoa thị là:
(đơn vị diện tích)
Diện tích hình tròn
Tổng diện tích hai hình viên phân và (ứng với các cung nhỏ).
Diện tích hình quạt tròn (ứng với cung nhỏ ).
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong tam giác vuông, bình phương một cạnh góc vuông bằng tích cạnh huyền với hình chiếu của cạnh góc vuông đó trên cạnh huyền.
+) Diện tích của một hình tròn bán kính được tính theo công thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
Lời giải:
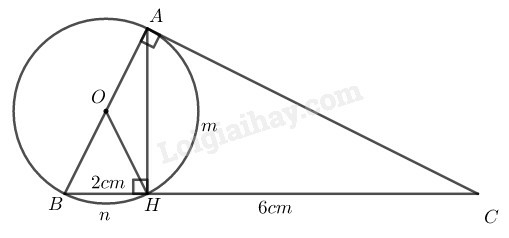
có
Theo hệ thức lượng trong tam giác vuông ta có:
Suy ra
Diện tích hình tròn tâm là:
Trong tam giác vuông ta có:
Suy ra
Tổng diện tích hai hình viên phân và bằng diện tích nửa hình tròn tâm trừ diện tích nên tổng diện tích hai hình viên phân là:
có
đều
(tính chất góc nội tiếp)
Bài tập bổ sung (trang 113 SBT Toán 9)
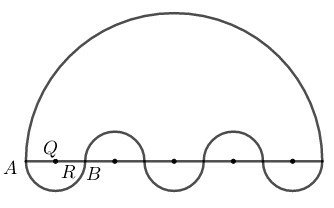
Phương pháp giải:
Ta sử dụng kiến thức: Diện tích của một hình tròn bán kính được tính theo công thức:
Lời giải:
Hình đó gồm nửa hình tròn bán kính nửa hình tròn bán kính và bớt đi nửa hình tròn bán kính
(đơn vị diện tích)