Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 9 Bài 10: Diện tích hình tròn, quạt tròn chọn lọc, có đáp án. Tài liệu có 14 trang gồm 30 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Diện tích hình tròn, quạt tròn có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.
Giới thiệu về tài liệu:
- Số trang: 14 trang
- Số câu hỏi trắc nghiệm: 30 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Diện tích hình tròn, quạt tròn có đáp án – Toán lớp 9:
Diện tích hình tròn, quạt tròn
Câu 1: Diện tích hình tròn bán kính R = 10cm là:
A. 100π (cm2)
B. 10π (cm2)
C. 20π (cm2)
D. 100π² 2 (cm2)
Lời giải:
Diện tích S = πR2 = π.102 = 100π (cm2)
Đáp án cần chọn là: A
Câu 2: Diện tích hình tròn bán kính R = 8cm là:
A. 8π (cm2)
B. 64π (cm2)
C. 16π (cm2)
D. 32π² 2 (cm2)
Lời giải:
Diện tích S = πR2 = π.82 = 64π (cm2)
Đáp án cần chọn là: B
Câu 3: Một hình tròn có diện tích S = 144π (cm2). Bán kính của hình tròn đó là:
A. 15 (cm)
B. 16 (cm)
C. 12 (cm)
D. 14 (cm)
Lời giải:
Diện tích S = πR2 = 144π ⇔ R2 = 144 ⇔ R = 12 (cm)
Đáp án cần chọn là: C
Câu 4: Một hình tròn có diện tích S = 225π (cm2). Bán kính của hình tròn đó là:
A. 15 (cm)
B. 16 (cm)
C. 12 (cm)
D. 14 (cm)
Lời giải:
Diện tích S = πR2 = 225π ⇔ R2 = 225 ⇔ R = 15 (cm)
Đáp án cần chọn là: A
Câu 5: Cho đường tròn (O; 10cm), đường kính AB. Điểm M ∈ (O) sao cho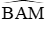 
= 45o. Tính diện tích hình quạt AOM
Lời giải:
Xét đường tròn (O) có:
Đáp án cần chọn là: B
Câu 6: Cho đường tròn (O; 8cm), đường kính AB. Điểm M ∈ (O) sao cho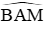 
= 60o. Tính diện tích hình quạt AOM
Lời giải:
Đáp án cần chọn là: C
Câu 7: Cho đường tròn (O) đường kính AB = 4√3 cm. Điểm C ∈ (O) sao cho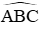 
= 30o. Tính diện tích hình viên phân AC. (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy)
Lời giải:
Xét đường tròn (O) có: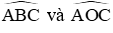 
là góc nội tiếp và góc ở tâm cùng chắn cung AC
Gọi CH là đường cao của tam giác AOC, ta có:
Đáp án cần chọn là: B
Câu 8: Cho đường tròn (O) đường kính AB = 3√3 cm. Điểm C ∈ (O) sao cho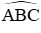 
= 60o. Tính diện tích hình viên phân BC. (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy)
Lời giải:
Xét đường tròn (O) có: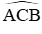 
= 90o (góc nội tiếp chắn nửa đường tròn)
Suy ra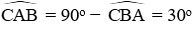 
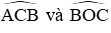
(tam giác ABC vuông tại C)
là góc nội tiếp và góc ở tâm cùng chắn cung AC
Gọi CH là đường cao của tam giác AOC, ta có:
Đáp án cần chọn là: A
Câu 9: Cho hình vuông có cạnh là 5cm nội tiếp đường tròn (O). Hãy tính diện tích hình tròn (O)
Lời giải:
Gọi hình vuông ABCD nội tiếp đường tròn (O) khi đó OA = OB = OC = OD = R ⇒ O là giao điểm của AC và BD 
Xét tam giác vuông ABC ta có:
Đáp án cần chọn là: D
Câu 10: Cho hình vuông có cạnh là 6 cm nội tiếp đường tròn (O). Hãy tính diện tích hình tròn (O)
A. 18π (cm2)
B. 36π (cm2)
C. 18π (cm2)
D. 36π (cm2)
Lời giải:
Gọi hình vuông ABCD nội tiếp đường tròn (O) khi đó OA = OB = OC = OD = R ⇒ O là giao điểm của AC và BD 
Xét tam giác vuông ABC ta có:
Đáp án cần chọn là: A
Câu 11: Cho đường tròn (O) đường kính AB = 2√2 cm. Điểm C ∈ (O) sao cho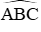 
= 30o. Tính diện tích hình giới hạn bởi đường tròn (O) và AC, BC
Lời giải:
Diện tích hình tròn (O) là S(O) = πR2
Ta có góc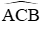 
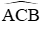
là góc nội tiếp chắn nửa đường tròn ⇒ = 90o
Giả sử CH là đường cao của tam giác ABH, ta có:
Diện tích hình giới hạn bởi đường tròn (O) và AC, BC là:
Đáp án cần chọn là: A
Câu 12: Cho đường tròn (O) đường kính AB = 4√2 cm. Điểm C ∈ (O) sao cho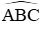 
= 30o. Tính diện tích hai hình viên phân giới hạn bởi đường tròn (O) và AC, BC
Lời giải:
Diện tích hình tròn (O) là S(O) = πR2
Ta có góc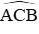 
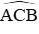
là góc nội tiếp chắn nửa đường tròn ⇒ = 90o
Giả sử CH là đường cao của tam giác ABH, ta có:
Diện tích hình giới hạn bởi đường tròn (O) và AC, BC là:
Đáp án cần chọn là: B
Câu 13: Cho đường tròn (O; R) và một điểm M sao cho OM = 2R. Từ M vẽ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Tính diện tích giới hạn bởi hai tiếp tuyến AM, MB và cung nhỏ AB
Lời giải:
Diện tích giới hạn bởi hai tiếp tuyến AM, MB và cung nhỏ AB là:
Đáp án cần chọn là: D
Câu 14: Cho đường tròn (O; R) và một điểm M sao cho OM = R√2. Từ M vẽ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Tính diện tích giới hạn bởi hai tiếp tuyến AM, MB và cung nhỏ AB
Lời giải:
Diện tích giới hạn bởi hai tiếp tuyến AM, MB và cung nhỏ AB là:
Đáp án cần chọn là: C
Câu 15: Một hình quạt có chu vi bằng 28 (cm) và diện tích bằng 49 (cm2). Bán kính của hình quạt bằng?
A. R = 5 (cm)
B. R = 6 (cm)
C. R = 7 (cm)
D. R = 8 (cm)
Lời giải:
Vậy R = 7 (cm)
Đáp án cần chọn là: C
Câu 16: Một hình quạt có chu vi bằng 34 (cm) và diện tích bằng 66 (cm2). Bán kính của hình quạt bằng?
A. R = 5 (cm)
B. R = 6 (cm)
C. R = 7 (cm)
D. R = 8 (cm)
Lời giải:
Vậy R = 6 (cm)
Đáp án cần chọn là: B
Câu 17: Cho tam giác đều ABC nội tiếp đường tròn (O). Độ dài các cung AB, BC, CA đều bằng 4π. Diện tích của tam giác đều ABC là?
A. 27√3 cm2.
B. 7√3 cm2.
C. 29√3 cm2.
D. 9√3 cm2.
Lời giải:
Gọi R là bán kính của đường tròn (O). Độ dài của các cung AB, BC, CA đều bằng 4π nên ta có: C = 2πR = 4π + 4π + 4π = 12π, suy ra R = 6 hay OA = OB = OC = 6
Kẻ đường cao OA, ta có đồng thời là đường trung tuyến, phân giác góc 
Đáp án cần chọn là: A
Câu 18: Cho tam giác đều ABC nội tiếp đường tròn (O). Độ dài các cung AB, BC, CA đều bằng 6π. Diện tích của tam giác đều ABC là?
Lời giải:
Gọi R là bán kính của đường tròn (O). Độ dài của các cung AB, BC, CA đều bằng 6π nên ta có: C = 2πR = 6π + 6π + 6π = 18π, suy ra R = 9 hay OA = OB = OC = 9
Kẻ đường cao OA, ta có đồng thời là đường trung tuyến, phân giác góc 
Đáp án cần chọn là: D
Câu 19: Cho A, B, C, D là 4 đỉnh của hình vuông có cạnh là a. Tính diện tích của hình hoa 4 cánh giới hạn bởi các đường tròn có bán kính bằng a, tâm là các đỉnh của hình vuông.
A. S = (π + 2)a2.
B. S = 2(π + 2)a2
C. S = (π − 2)a2
D. S = 2(π − 2)a2
Lời giải:
Ta có diện tích của hình hoa cần tính bằng 4 lần diện tích của hình viên phân AC:
S = 4Svp AC.
Đáp án cần chọn là: C
Câu 20: Cho A, B, C, D là 4 đỉnh của hình vuông có cạnh là 2 cm. Tính diện tích của hình hoa 4 cánh giới hạn bởi các đường tròn có bán kính bằng 2 cm, tâm là các đỉnh của hình vuông.
A. S = 4π − 8
B. S = 4π + 8
C. S = 4π
D. S = 8 − 4π
Lời giải:
Ta có diện tích của hình hoa cần tính bằng 4 lần diện tích của hình viên phân AC:
S = 4Sviên phân AC.
Hình viên phân AC bằng Squạt ADC − S∆ADC
Quạt tròn ADC có DA = DC = 3cm và số đo cung 90o
Đáp án cần chọn là: A
Bài giảng Toán 9 Bài 10: Diện tích hình tròn hình quạt tròn
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
