Với giải Bài 83 trang 99 Toán lớp 9 chi tiết trong Bài 10: Diện tích hình tròn, hình quạt tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 10: Diện tích hình tròn, hình quạt tròn

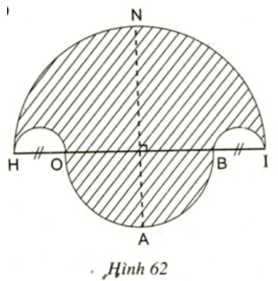
Bài 83 trang 99 SGK Toán lớp 9 Tập 2: a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = BI = 2cm. Nêu cách vẽ.

b) Tính diện tích hình HOABINH (miền gạch sọc).

c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó.

Lời giải:

a)

Cách vẽ

- Vẽ nửa đường tròn đường kính HI = 10cm, tâm M.

- Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.

- Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).

- Vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đường tròn đường kính OB tại A.

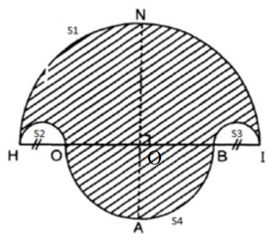
b)

$S_1$ là diện tích của nửa đường tròn đường kính HI nên ta có:

$$\begin{gathered} S_1=\frac{1}{2}\pi {\left(\frac{HI}{2}\right)}^2=\frac{1}{2}\pi {\left(\frac{10}{2}\right)}^2 \\ =12,5\pi \left(c{m}^2\right) \end{gathered}$$

$S_2, S_3$ là diện tích của nửa đường tròn đường kính HO và BI với HO = BI = 2cm nên ta có:

$$\begin{gathered} S_2=S_3=\frac{1}{2}\pi {\left(\frac{HO}{2}\right)}^2 \\ =\frac{1}{2}\pi {\left(\frac{2}{2}\right)}^2=0,5\pi \left(c{m}^2\right) \end{gathered}$$

$S_4$ là diện tích của nửa đường tròn đường kính OB nên ta có:

$$\begin{gathered} S_4=\frac{1}{2}\pi {\left(\frac{OB}{2}\right)}^2 \\ =\frac{1}{2}\pi {\left(\frac{HI-OH-BI}{2}\right)}^2 \\ =\frac{1}{2}\pi {\left(\frac{10-2-2}{2}\right)}^2=4,5\pi \left(c{m}^2\right) \end{gathered}$$

Diện tích miền gạch sọc là:

$$\begin{gathered} S=S_1-\left(S_2+S_3\right)+S_4 \\ =12,5\pi -(0,5\pi +0,5\pi )+4,5\pi \\ =16\pi \left(c{m}^2\right) \end{gathered}$$

c)

Điểm N thuộc hình tròn có diện tích $S_1$

Điểm A thuộc hình tròn có diện tích $S_4$

Ta có:  

$$\begin{gathered} NA=ON+OA \\ =\frac{HI}{2}+\frac{OB}{2} \\ =\frac{HI}{2}+\frac{HI-BI-HO}{2} \\ =\frac{10}{2}+\frac{10-2-2}{2}=8 \left(cm\right) \end{gathered}$$

Diện tích hình tròn đường kính NA là:

$$\begin{gathered} S\text{'}=\pi .{\left(\frac{NA}{2}\right)}^2 \\ =\pi .{\left(\frac{8}{2}\right)}^2=16\pi \left(c{m}^2\right)=S \end{gathered}$$

Vậy hình tròn đường kính NA có cùng diện tích với hình HOABINH đó.