Với giải bài 18 trang 75 Toán lớp 8 chi tiết trong Bài 3: Hình thang cân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 3: Hình thang cân

Bài 18 trang 75 sgk Toán 8 Tập 1: Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang $ABCD$ $\left(AB//C\mathrm{D}\right)$ có $AC=BD.$

Qua $B$ kẻ đường thẳng song song với $AC$, cắt đường thẳng $DC$ tại $E.$ Chứng mình rằng:

a) $∆BDE$ là tam giác cân.

b) $∆ACD=∆BDC.$

c) Hình thang $ABCD$ là hình thang cân.

Phương pháp giải: Áp dụng:

- Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.

- Tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.

- Nhận xét: Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.

Lời giải:

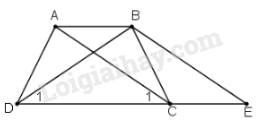
a) $E$ thuộc đường thẳng $DC$ nên $CE//AB.$

Hình thang $ABEC(AB//CE)$ có hai cạnh bên $AC,BE$ song song (giả thiết) $\Rightarrow AC=BE$  (1)  (nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau )

Lại có: $AC=BD$ (giả thiết)   (2)

Từ (1) và (2) suy ra $BE=BD$ $\Rightarrow \mathrm{\Delta }BED$ cân tại $B$ (dấu hiệu nhận biết tam giác cân).

b) Ta có $AC//BE\Rightarrow \widehat{C_1}=\hat{E}$ (2 góc đồng vị) (3)

$∆BDE$ cân tại $B$ (chứng minh trên) $\Rightarrow \widehat{D_1}=\hat{E}$ (4)

Từ (3) và (4) $\Rightarrow \widehat{D_1}=\widehat{C_1}$

Xét $∆ACD$ và $∆BDC$ có:

+) $AC=BD$ (giả thiết)

+) $\widehat{C_1}=\widehat{D_1}$ (chứng minh trên)

+) $CD$ chung

Suy ra $∆ACD=∆BDC$ (c.g.c)

c) Ta có: $∆ACD=∆BDC$ (chứng minh trên)

$\Rightarrow \widehat{A\mathrm{D}C}=\widehat{BCD}$ ($2$ góc tương ứng)

Hình thang $ABCD$ có hai góc kề một đáy bằng nhau nên là hình thang cân.

Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác: