Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác

Đức Long Ngày: 12-10-2022 Lớp 8

1.7 K

Với giải bài 2 trang 66 Toán lớp 8 chi tiết trong Bài 1: Tứ giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 1: Tứ giác

Bài 2 trang 66 sgk Toán 8 tập 1: Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.

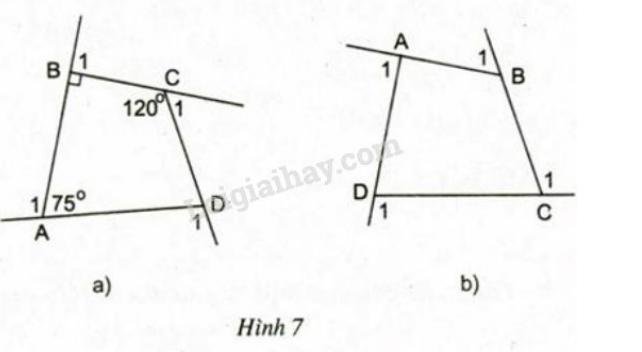
Giải Toán 8 Bài 1: Tứ giác (ảnh 6)

a) Tính các góc ngoài của tứ giác ở hình 7a.

Phương pháp giải: Áp dụng định lý: Tổng các góc trong tứ giác bằng $360^{0}$

Lời giải:

$\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360^{0}$ (định lý tổng các góc của tứ giác)

$\begin{array}{l} \hat{D} = 360^{0} - (\hat{A} + \hat{B} + \hat{C}) \\ = 360^{0} - (75^{0} + 90^{0} + 120^{0}) \\ = 360^{0} - 285^{0} \\ = 75^{0} \end{array}$

Ta có:

+) $\hat{B A D} + \hat{A_{1}} = 180^{0}$ (2 góc kề bù)

$\begin{array}{l} \hat{A_{1}} = 180^{0} - \hat{B A D} \\ = 180^{0} - 75^{0} = 105^{0} . \end{array}$

+) $\hat{B_{1}} + \hat{C B A} = 180^{0}$ (2 góc kề bù)

$\begin{array}{l} \hat{B_{1}} = 180^{0} - \hat{C B A} \\ = 180^{0} - 90^{0} = 90^{0} . \end{array}$

+) $\hat{C_{1}} + \hat{B C D} = 180^{0}$ (2 góc kề bù)

$\begin{array}{l} \hat{C_{1}} = 180^{0} - \hat{B C D} \\ = 180^{0} - 120^{0} = 60^{0} . \end{array}$

+) $\hat{D_{1}} + \hat{A D C} = 180^{0}$

$\begin{array}{l} \hat{D_{1}} = 180^{0} - \hat{A D C} \\ = 180^{0} - 75^{0} = 105^{0} . \end{array}$

b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài): $\hat{A_{1}} + \hat{B_{1}} + \hat{C_{1}} + \hat{D_{1}} = ?$

Phương pháp giải: Áp dụng định lý: Tổng các góc trong tứ giác bằng $360^{0}$

Lời giải:

Ta có:

+) $\hat{A} + \hat{A_{1}} = 180^{0}$ (2 góc kề bù) $\Rightarrow \hat{A_{1}} = 180^{0} - \hat{A}$

+) $\hat{B} + \hat{B_{1}} = 180^{0}$ (2 góc kề bù) $\Rightarrow \hat{B_{1}} = 180^{0} - \hat{B}$

+) $\hat{C} + \hat{C_{1}} = 180^{0}$ (2 góc kề bù) $\Rightarrow \hat{C_{1}} = 180^{0} - \hat{C}$

+) $\hat{D} + \hat{D_{1}} = 180^{0}$ (2 góc kề bù) $\Rightarrow \hat{D_{1}} = 180^{0} - \hat{D}$

Lại có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360^{0}$ (định lý tổng 4 góc trong tứ giác ABCD)

Ta có:

$\begin{array}{l} \hat{A_{1}} + \hat{B_{1}} + \hat{C_{1}} + \hat{D_{1}} \\ = (180^{0} - \hat{A}) + (180^{0} - \hat{B}) \\ + (180^{0} - \hat{C}) + (180^{0} - \hat{D}) \\ = 180^{0} .4 - (\hat{A} + \hat{B} + \hat{C} + \hat{D}) \\ = 720^{0} - 360^{0} = 360^{0} . \end{array}$