Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 1 Bài 1: Tứ giác. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 1: Tứ giác. Mời các bạn đón xem:

Bài tập Toán 8 Chương 1 Bài 1: Tứ giác

A. Bài tập Tứ giác

I. Bài tập trắc nghiệm

Bài 1: Cho tứ giác ABCD, trong đó $\hat{A}$ˆ + $\hat{B}$ = 140⁰. Tổng $\hat{C}$ + $\hat{D}$ˆ = ?

A. 220⁰   

B. 200⁰

C. 160⁰   

D. 150⁰

Lời giải:

Định lí: Tổng các góc của một tứ giác bằng 3600.

Khi đó ta có $\hat{A}+\hat{B}+\hat{C}+\hat{D}$ˆ = 360⁰ ⇒ ( $\hat{C}+\hat{D}$ˆ ) = 360⁰ - ( $\hat{A}+\hat{B}$ˆ ) = 360⁰ - 140⁰ = 220⁰

Chọn đáp án A.

Bài 2: Số đo các góc của tứ giác ABCD theo tỷ lệ $\hat{A}:\hat{B}:\hat{C}:\hat{D}$ = 4:3:2:1. Số đo các góc theo thứ tự đó là ?

A. 120⁰;90⁰;60⁰;30⁰.

B. 140⁰;105⁰;70⁰;35⁰.

C. 144⁰;108⁰;72⁰;36⁰.

D. Cả A, B, C đều sai.

Lời giải:

Định lí: Tổng các góc của một tứ giác bằng 360⁰.

Theo giải thiết ta có $\hat{A}:\hat{B}:\hat{C}:\hat{D}$ = 4:3:2:1 ⇒ $\hat{A}=4\hat{D}$ˆ; $\hat{B}=3\hat{D}$;$\hat{C}=2\hat{D}$ˆ

Khi đó ta có $\hat{A}+\hat{B}+\hat{C}+\hat{D}$ˆ = 360⁰ ⇔ $4\hat{D}+3\hat{D}+2\hat{D}+\hat{D}$ˆ = 360⁰

⇔ $10\hat{D}$ˆ = 360⁰ ⇔ $\hat{D}$ˆ = 360⁰.

Chọn đáp án C.

Bài 3: Chọn câu đúng trong các câu sau:

A. Tứ giác ABCD có 4 góc đều nhọn.

B. Tứ giác ABCD có 4 góc đều tù.

C. Tứ giác ABCD có 2 góc vuông và 2 góc tù.

D. Tứ giác ABCD có 4 góc đều vuông.

Lời giải:

Theo định lí: Tổng các góc của một tứ giác bằng 360⁰.

Nhận xét:

+ α là góc nhọn thì 0⁰ < α < 90⁰ ⇒ 0⁰ < 4.α < 360^0.

⇒ Không tồn tại tứ giác ABCD có 4 góc đều nhọn. ⇒ Loại A.

+ α là góc tù thì 90⁰ < α < 180⁰ ⇒ 360⁰ < 4.α < 720⁰

⇒ Không tồn tại tứ giác ABCD có 4 góc đều tù. ⇒ Loại B.

+ α là góc vuông thì α = 90⁰; β là góc tù thì 90⁰ < β < 180⁰ ⇒ 180⁰

Khi đó ta có : 180⁰ + 180⁰ < 2α + 2β < 180⁰ + 360⁰

⇒ 360⁰ < 2α + 2β < 540⁰

⇒ Không tồn tại tứ giác ABCD có 2 góc nhọn và 2 góc tù. ⇒ Loại C.

+ Vì tứ giác có 4 góc vuông thì tổng các góc bằng 360⁰.

Chọn đáp án D.

Bài 4: Cho tứ giác ABCD có $\hat{A}$ˆ = 65⁰;$\hat{B}$ = 117⁰;$\hat{C}$ = 71⁰. Số đo góc D = ?

A. 119⁰. 

B. 107⁰.

C. 63⁰.   

D. 126⁰

Lời giải:

Định lí: Tổng các góc của một tứ giác bằng 360⁰.

Khi đó ta có $\hat{A}+\hat{B}+\hat{C}+\hat{D}$ = 360⁰ ⇒ $\hat{D}$ = 360⁰ - ( $\hat{A}+\hat{B}+\hat{C}$) = 360⁰ - ( 65⁰ + 117⁰ + 71⁰ )

⇒ Dˆ = 360⁰ - 253⁰ = 107⁰.

Chọn đáp án B.

Bài 5: Cho tứ giác ABCD trong đó có $\hat{B}$ = 75⁰;$\hat{D}$ˆ = 120⁰. Khi đó $\hat{A}+\hat{C}$ˆ = ?

A. 190⁰   

B. 130⁰

C. 215⁰   

D. 165⁰

Lời giải:

Định lí: Tổng các góc của một tứ giác bằng 360⁰.

Khi đó ta có $\hat{A}+\hat{B}+\hat{C}+\hat{D}$ = 360⁰ ⇒ ($\hat{C}+\hat{A}$ˆ ) = 360⁰ - ( $\hat{B}+\hat{D}$ ) = 360⁰ - 195⁰ = 165⁰

Chọn đáp án D.

Bài 6: Xét tứ giác ABCD có $\hat{A}=\hat{D}$ˆ; $\hat{B}$ˆ = 50^o; $\hat{C}$ˆ = 90^o . Tính $\hat{A}$ˆ

A. 110^o  

B. 100^o

C. 120^o    

D. 90^o

Chọn đáp án A

Bài 7: Cho tứ giác ABCD có $\widehat{A }=\hat{C}=\hat{D}$ˆ = 80^o . Góc $\hat{B}$ˆ là góc?

A. Góc nhọn    

B. Góc vuông

C. Góc tù    

D. Góc bẹt

Chọn đáp án C

Bài 8: Cho tứ giác ABCD có $\hat{B}$$+ \hat{C}$ = 150^o; $\hat{A}$$=\hat{D}$ˆ. Tính góc $\hat{D}$?

A. 105^o    

B. 100^o

C. 120^o    

D. 75^o

Lời giải:

Chọn đáp án A

Bài 9: Cho tứ giác ABCD có $\hat{A}=2\hat{B}=2\hat{C}=\hat{D}$ˆ . Tính số đo góc $\hat{A}$?

A. 90^o    

B. 150^o

C. 120^o    

D. 160^o

Lời giải:

Chọn đáp án C

Bài 10: Cho tứ giác ABCD có $\hat{A}=2\hat{B}$ˆ = 120^o; $\hat{C}=2\hat{D}$ˆ. Tính $\hat{D}$ˆ

A. 45^o    

B. 90^o

C. 120^o    

D. 60^o

Lời giải:

Chọn đáp án D

Bài 11: Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là

A. 300⁰       

B. 270⁰       

C. 180⁰       

D. 360⁰

Lời giải:

Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là 

Vậy tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là 360⁰.

Đáp án cần chọn là: D

Bài 12: Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là 200⁰. Tổng số đo các góc ngoài tại 2 đỉnh A, C là:

A. 160⁰           

B. 260⁰           

C. 180⁰           

D. 100⁰

Lời giải:

Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là 

Vậy tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là 360⁰.

Mà tổng số đo góc ngoài tại hai đỉnh B, C bằng 200⁰ nên tổng số đo góc ngoài tại hai đỉnh A, D bằng 360⁰ – 200⁰ = 160⁰.

Đáp án cần chọn là: A

Bài 13: Cho tứ giác ABCD có  = 100⁰. Tổng số đo các góc ngoài đỉnh B, C, D bằng:

A. 180⁰           

B. 260⁰           

C. 280⁰           

D. 270⁰

Lời giải

Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là 

Đáp án cần chọn là: C

Bài 14: Cho tứ giác ABCD có  = 80⁰. Tổng số đo các góc ngoài đỉnh B, C, D bằng:

A. 180⁰           

B. 260⁰           

C. 280⁰           

D. 270⁰

Lời giải:

Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là 

Đáp án cần chọn là: B

Bài 15: Tứ giác ABCD có AB = BC, CD = DA, 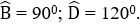 Hãy chọn câu đúng nhất:

Lời giải

Đáp án cần chọn là: D

II. Bài tập tự luận

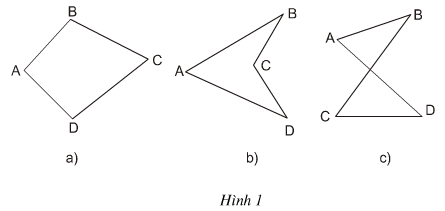
Bài 1. Trong các tứ giác ở hình 1, tứ giác nào luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác?

Lời giải:

a) Tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác

b) Tứ giác nằm trên hai nửa mặt phẳng có bờ BC (hoặc bờ CD)

c) Tứ giác nằm trên hai nửa mặt phẳng có bờ AD (hoặc bờ BC)

Bài 2. Quan sát tứ giác ABCD ở hình 3 rồi điền vào chỗ trống:

a) Hai đỉnh kề nhau: A và B, …

Hai đỉnh đối nhau: A và C, …

b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, …

c) Hai cạnh kề nhau: AB và BC, …

Hai cạnh đối nhau: AB và CD, …

d) Góc: $\hat{A}$, …

Hai góc đối nhau: $\hat{A}$ và $\hat{C}$ , …

e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, …

Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, …

Lời giải:

a) Hai đỉnh kề nhau: A và B, B và C, C và D, D và A

Hai đỉnh đối nhau: A và C, B và D

b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, BD

c) Hai cạnh kề nhau: AB và BC, BC và CD, CD và DA, DA và AB

Hai cạnh đối nhau: AB và CD, AD và BC

d) Góc: $\hat{A}, \hat{B}, \hat{C}, \hat{D}$

Hai góc đối nhau: $\hat{A}$ và $\hat{C}$, $\hat{B}$ và $\hat{D}$

e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, P

Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, Q

Bài 3. a) Nhắc lại định lý về tổng ba góc của một tam giác

b) Vẽ tứ giác ABCD tùy ý. Dựa vào định lý về tổng ba góc của một tam giác, hãy tính tổng $\hat{A}+\hat{B}+\hat{C}+\hat{D}$

Lời giải:

a) Trong một tam giác, tổng ba góc là 180^o

b)

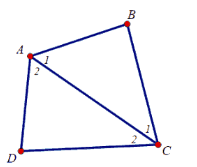
ΔABC có $\widehat{A_1}+\widehat{B_1}+\widehat{C_1}$ = 180^o

ΔADC có ${\hat{A}}_2+\hat{D}+\widehat{C_2}$ = 180^o

⇒ $\widehat{A_1 }+ \hat{B} + \widehat{C_1} + \widehat{A_2} + \hat{D} + \widehat{C_2}$ = 180^o + 180^o

⇒ $\widehat{(A_1} + \widehat{A_2} ) + \hat{B} + (\widehat{C_1 }+ \widehat{C_2}) + \hat{D}$ = 360^o

⇒ $\hat{A} + \hat{B} + \hat{C} + \hat{D}$ = 360^o

Bài 4. Tìm x ở hình 5, hình 6:

 

Lời giải:

(Áp dụng: tổng 4 góc trong một tứ giác bằng 360^o)

- Ở hình 5:

a) x = 360^o - (110^o + 120^o + 80^o) = 50^o

b) x = 360^o - (90^o + 90^o + 90^o) = 90^o

c) x = 360^o - (90^o + 90^o + 65^o) = 115^o

d) x = 360^o - (75^o + 120^o + 90^o) = 75^o

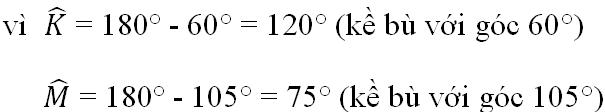
- Ở hình 6:

a) x + x = 360^o - (65^o + 95^o)

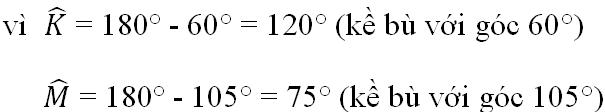
b) 2x + 3x + 4x + x = 360^o

=> 10x = 360^o

=> x = 36^o

Bài 5. Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.

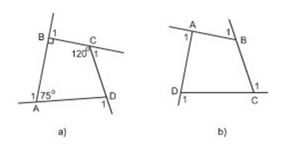
a) Tính các góc ngoài của tứ giác ở hình 7a.

b) Tính tổng các góc ngoài của tứ giác ở hình 7b ( tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):

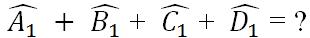
c) Có nhận xét gì về tổng các góc ngoài của tứ giác?

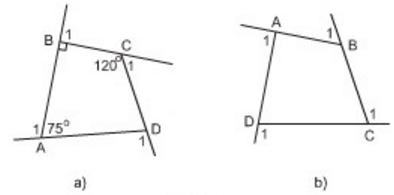
Lời giải:

+ Góc ngoài tại $\hat{A}$ là góc $\widehat{A_1}$:

+ Góc ngoài tại $\hat{B}$ là góc $\widehat{B_1}$:

+ Góc ngoài tại $\hat{C}$ là góc $\widehat{C_1}$:

+ Góc ngoài tại $\hat{D}$ là góc $\widehat{D_1}$:

Theo định lý tổng các góc trong một tứ giác bằng 360º ta có:

Lại có:

Vậy góc ngoài tại $\hat{D}$ bằng 105º.

b) Hình 7b:

Ta có:

Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:

c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.

Bài 6. Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều".

a) Chứng minh rằng AC là đường trung trực của BD.

b) Tính B̂,D̂ biết rằng  = 100º, Ĉ = 60º

Lời giải:

a) Ta có:

AB = AD (gt) => A thuộc đường trung trực của BD

CB = CD (gt) => C thuộc đường trung trực của BD

Vậy AC là đường trung trực của BD

b) Xét ΔABC và ΔADC có:

AB = AD (gt)

BC = DC (gt)

AC cạnh chung

=> ΔABC = ΔADC (c.c.c)

Suy ra:

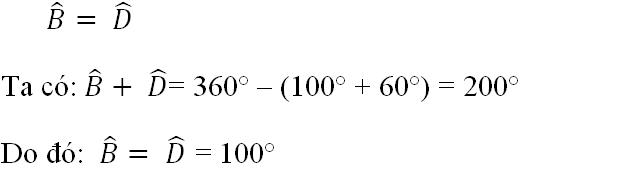
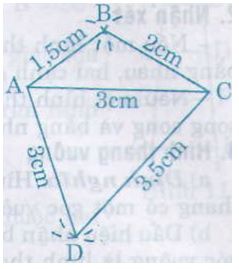
Bài 7. Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở.

 

Lời giải:

- Cách vẽ hình 9: Vẽ tam giác ABC trước rồi vẽ tam giác ACD (hoặc ngược lại).

+ Vẽ đoạn thẳng AC = 3cm.

+ Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm với cung tròn tâm C bán kính 2cm.

+ Hai cung tròn trên cắt nhau tại B.

+ Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.

Tương tự ta vẽ được tam giác ACD. Tứ giác ABCD là tứ giác cần vẽ.

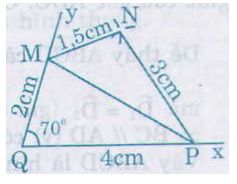
- Cách vẽ hình 10: Vẽ tam giác MQP trước rồi vẽ tam giác MNP. Vẽ tam giác MQP biết hai cạnh và góc xen giữa.

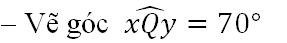
+ Trên tia Qx lấy điểm M sao cho QM = 2cm.

+ Trên tia Qy lấy điểm P sao cho QP = 4cm.

+ Vẽ đoạn thẳng MP, ta được tam giác MPQ.

Vẽ tam giác MNP biết ba cạnh, với cạnh MP đã vẽ. Tương tự cách vẽ hình 10, điểm N là giao điểm của hai cung tròn tâm M, P bán kính lần lượt là 1,5cm; 3cm.. Tứ giác MNPQ là tứ giác cần vẽ.

Bài 8. Đố. Đố em tìm thấy vị trí của "kho báu" trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3; 2), B(2; 7), C(6; 8), D(8; 5).

Lời giải:

Đánh dấu các số thứ tự (như trục tọa độ) và kí hiệu các điểm như trên hình. Các bước làm như sau:

- Xác định các điểm A, B, C, D trên hình vẽ với A(3; 2); B(2; 7); C(6; 8); D(8; 5).

- Vẽ tứ giác ABCD

- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.

- Xác định tọa độ của điểm K: K(5; 6)

Bài 9 Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.

a) Tính các góc ngoài của tứ giác trong hình 7a.

b) Tính tổng các góc ngoài của tứ giác trong hình 7b ( tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):

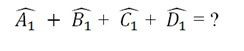
c) Có nhận xét gì về tổng của các góc ngoài của tứ giác?

Lời giải:

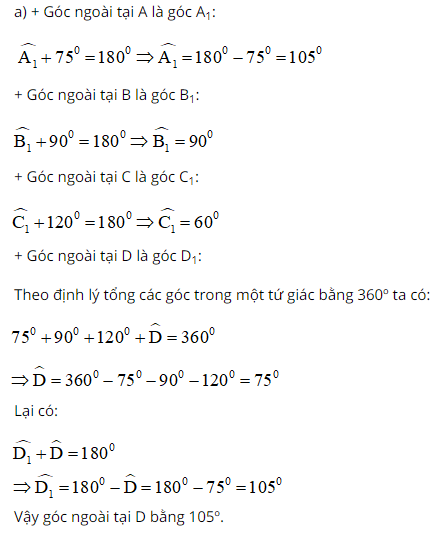
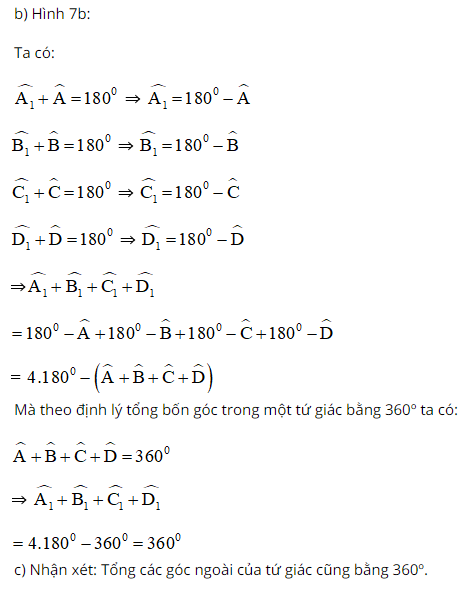
Bài 10 Tìm x ở hình 5, hình 6:

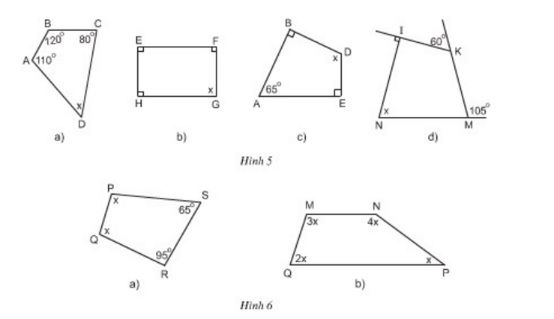
Lời giải:

(Gợi ý: tổng 4 góc trong một tứ giác bằng 360^o)

- Trong hình 5:

Ta có định lý: Tổng bốn góc trong một tứ giác bằng 360º.

+ Hình 5a: Áp dụng định lý trong tứ giác ABCD ta có:

x + 110º + 120º + 80º = 360º

⇒ x = 360º – 110º – 120º – 80º = 50º

+ Hình 5b: Áp dụng định lý trong tứ giác EFGH ta có:

x + 90º + 90º + 90º = 360º

⇒ x = 360º – 90º – 90º – 90º = 90º.

+ Hình 5c: Áp dụng định lý trong tứ giác ABDE ta có:

x + 90º + 65º + 90º = 360º

⇒ x = 360º – 90º – 65º – 90º = 115º

+ Hình 5d:

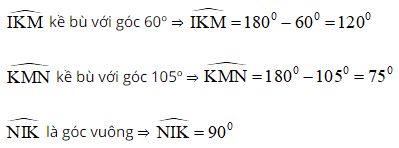
Áp dụng định lý trong tứ giác IKMN ta có:

x + 90º + 120º + 75º = 360º

⇒ x = 360º – 90º – 120º – 75º = 75º

+ Hình 6a: Áp dụng định lý trong tứ giác PQRS ta có:

x + x + 65º + 95º = 360º

⇒ 2x + 160º = 360º

⇒ 2x = 200º

⇒ x = 100º

+ Hình 6b: Áp dụng định lý trong tứ giác MNPQ ta có:

x + 2x + 3x + 4x = 360º

⇒ 10x = 360º

⇒ x = 36º.

Bài 11 Ta gọi tứ giác ABCD ở hình 8 có AB = AD, CB = CD là hình "cái diều".

a) Chứng minh rằng AC là đường trung trực của BD.

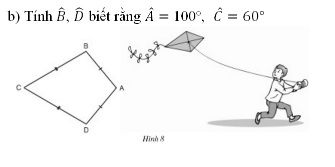
Lời giải:

a) Ta có:

AB = AD (gt) suy ra A thuộc đường trung trực của BD

CB = CD (gt) suy ra C thuộc đường trung trực của BD

Vậy AC là đường trung trực của BD

b) Xét ΔABC và ΔADC có:

AB = AD (gt)

BC = DC (gt)

AC cạnh chung

=> ΔABC = ΔADC (c.c.c)

Suy ra:

Bài 12 Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở.

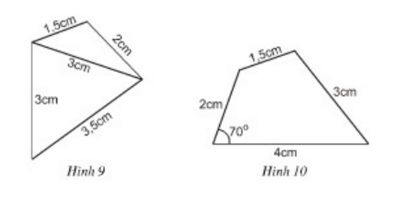
Lời giải:

- Cách vẽ hình 9: Vẽ tam giác ABC trước sau đó vẽ tam giác ACD (hoặc ngược lại).

+ Vẽ đoạn thẳng AC = 3cm.

+ Trên cùng nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm với cung tròn tâm C bán kính 2cm.

+ Hai cung tròn trên cắt nhau ở B.

+ Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.

Tương tự ta vẽ tam giác ACD. Ta được tứ giác ABCD là tứ giác cần vẽ.

- Cách vẽ hình 10: Vẽ tam giác MQP trước sau đó vẽ tam giác MNP. Vẽ tam giác MQP biết hai cạnh và góc xen giữa.

+ Trên tia Qx lấy điểm M với QM = 2cm.

+ Trên tia Qy lấy điểm P với QP = 4cm.

+ Vẽ đoạn thẳng MP, ta được tam giác MPQ.

Vẽ tam giác MNP biết 3 cạnh, với cạnh MP đã vẽ. Tương tự cách vẽ trên, điểm N là giao điểm giữa 2 cung tròn tâm M, P bán kính lần lượt là 1,5cm; 3cm.. Ta được tứ giác MNPQ là tứ giác cần vẽ.

Bài 13. Trong các tứ giác ở hình 1, tứ giác nào luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác?

Lời giải:

Tứ giác hình a luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác

Tứ giác hình b nằm trên hai nửa mặt phẳng có bờ BC (hoặc bờ CD)

Tứ giác hình c nằm trên hai nửa mặt phẳng có bờ AD (hoặc bờ BC)

Bài 14. Quan sát tứ giác ABCD ở hình 3 rồi điền vào chỗ trống:

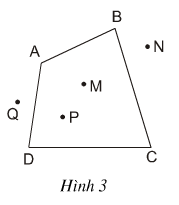
a) Hai đỉnh kề nhau: A và B, …

Hai đỉnh đối nhau: A và C, …

b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, …

c) Hai cạnh kề nhau: AB và BC, …

Hai cạnh đối nhau: AB và CD, …

d) Góc: $\hat{A}$ , …

Hai góc đối nhau: $\hat{A}$ và $\hat{C}$ , …

e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, …

Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, …

Lời giải:

a) Hai đỉnh kề nhau: A và B, B và C, C và D, D và A

Hai đỉnh đối nhau: A và C, B và D

b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, BD

c) Hai cạnh kề nhau: AB và BC, BC và CD, CD và DA, DA và AB

Hai cạnh đối nhau: AB và CD, AD và BC

d) Góc: $\hat{A} , \hat{B} , \hat{C} , \hat{D}$

Hai góc đối nhau: $\hat{A}$ và $\hat{C}$ , $\hat{B}$ và $\hat{D}$

e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, P

Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, Q

Bài 15

a) Nhắc lại định lý về tổng ba góc của một tam giác

b) Vẽ tứ giác ABCD tùy ý. Dựa vào định lý về tổng ba góc của một tam giác, hãy tính tổng $\hat{A}+\hat{B}+\hat{C}+\hat{D}$

Lời giải:

a) Trong một tam giác, tổng ba góc bằng 180^o

b)

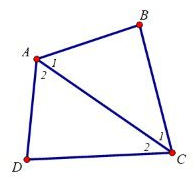
ΔABC có $\widehat{A_1} + \hat{B} + \widehat{C_1}$ = 180^o

ΔADC có $\widehat{A_2} + \hat{D} + \widehat{C_2}$ = 180^o

⇒ $\widehat{A_1} + \hat{B} + \widehat{C_1} + \widehat{A_2} + \hat{D} + \widehat{C_2}$ = 180^o + 180^o

⇒$(\widehat{A_1} + \widehat{A_2} ) + \hat{B} + (\widehat{C_1} + \widehat{C_2}) +\hat{D}$ = 360^o

⇒ $\hat{A} + \hat{B} + \hat{C} + \hat{D}$ = 360^o

III. Bài tập vận dụng

Bài 1. Tìm x ở trên hình a và b

Bài 2 Góc kề bù với một góc trong của tứ giác gọi là góc ngoài của tứ giác.

a) Tính các góc ngoài của tứ giác ở hình.

b) Có nhận xét gì về tổng các góc ngoài của tứ giác.

Bài 3 Cho tứ giác ABCD có: $\hat{B}={120}^{\circ };\hat{C}={50}^{\circ };\hat{D}={90}^{\circ }$. Tính góc $\hat{A}$ và góc ngoài tứ giác tại đỉnh A.

Bài 4 Tứ giác BCDE có: $\hat{B}={120}^{\circ };\hat{C}={50}^{\circ };\hat{D}-\hat{E}={40}^{\circ }$. Tính $\hat{D};\hat{E}$

Bài 5 Tính các góc của tứ giác EFGH biết:

$\hat{E}:\hat{F}:\hat{G}:\hat{H}=1:2:4:5$

Bài 6: Cho tứ giác ABCD, trong đó $\hat{A}+\hat{B}$ˆ = 140⁰. Tổng $\hat{C}+\hat{D}$ˆ = ?

Bài 7 Cho tứ giác ABCD có $\hat{A}$ˆ = 65⁰;$\hat{B}$ˆ = 117⁰;$\hat{C}$ˆ = 71⁰. Số đo góc $\hat{D}$

Bài 8: Cho tứ giác ABCD có $\hat{A}=\hat{C}=\hat{D}$ˆ = 80^o . Góc $\hat{B}$ˆ là góc?

Bài 9 Cho tứ giác ABCD có $\hat{B}+\hat{C}$ˆ = 150^o; $\hat{A}=\hat{D}$ˆ. Tính góc $\hat{D}$?

Bài 10 Cho tứ giác ABCD có $\hat{A}=2\hat{B}$ˆ = $2\hat{C}=\hat{D}$. Tính số đo góc $\hat{A}$?

Bài 11 Cho tứ giác ABCD có $\hat{A}=2\hat{B}$ = 120^o; $\hat{C}=2\hat{D}$ˆ. Tính $\hat{D}$

Bài 12 Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là

Bài 13 Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.

a) Tính các góc ngoài của tứ giác ở hình 7a.

b) Tính tổng các góc ngoài của tứ giác ở hình 7b ( tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):

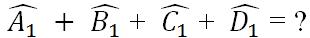
c) Có nhận xét gì về tổng các góc ngoài của tứ giác?

Bài 14 Một hình thang có hiệu của đáy lớn và đáy bé bằng 21cm, đáy bé bằng 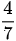 đáy lớn, chiều cao bằng  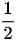đáy bé. Hãy tìm diện tích của hình thang nói trên.

Bài 15Một hình thang vuông có đáy bé bằng 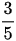 đáy lớn và chiều cao bằng 23cm, người ta mở rộng hình thang để được một hình chữ nhật thì diện tích của nó tăng thêm lên 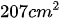. Hãy tính diện tích hình thang lúc đầu.

Bài 16 Một miếng đất hình thang có diện tích 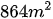, đáy lớn hơn đáy bé 12m. Người ta mở rộng miếng đất bằng cách tăng đáy lớn thêm 5m thì được miếng đất hình thang có diện tích bằng 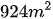. Tìm độ dài đáy lớn, đáy bé của miếng đất hình thang lúc chưa mở rộng.

Bài 17 Cho hình thang ABCD có diện tích 1000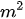. Trên cạnh bên AD lấy hai điểm M, N sao cho AM bằng ND và bằng 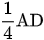. Từ M và N kẻ các đường song song với hai đáy AB và CD, chúng lần lượt cắt cạnh BC tại P và Q. Tính diện tích hình tứ giác MNQP.

Bài 18 Cho hình thang ABCD có diện tích 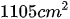, đáy lớn 47cm, đáy bé 38cm. Đoạn đường BD chia hình thang thành hai tam giác ABD và BCD. Hãy tính diện tích mỗi tam giác.

Bài 19 Một hình thang có diện tích 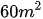, hiệu của hai đáy bằng 4m. Hãy tính độ dài mỗi đáy, biết rằng nếu đáy lớn được tăng thêm 2m thì diện tích hình thang sẽ tăng thêm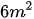 

Bài 20 Một thửa ruộng hình thang có diện tích là 1155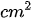 và có đáy bé kém đáy lớn 33m. Người ta kéo dài đáy bé thêm 20m và kéo dài đáy lớn thêm 5m về cùng một phía để được hình thang mới. Diện tích hình thang mới này bằng diện tích của một hình chữ nhật có chiều rộng là 30m và chiều dài 51m. Hãy tính đáy bé, đáy lớn của thửa ruộng ban đầu.

B. Lý thuyết Tứ giác

1. Định nghĩa tứ giác

Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Chú ý:

   Tứ giác ABCD còn được gọi tên là tứ giác BCDA,ADCB, ... . Các điểm A,B,C,D được gọi là các đỉnh. Các đoạn thẳng AB,BC,CD,DA được gọi là các cạnh.

   Tứ giác ABCD trên hình gọi là tứ giác lồi.

Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác

2. Tổng các góc của một tứ giác

Định lí: Tổng các góc của một tứ giác bằng 360⁰.

Tổng quát: Aˆ + Bˆ + Cˆ + Dˆ = 360⁰.

Ví dụ: Cho tứ giác ABCD trong đó có Aˆ = 60⁰,Cˆ = 150⁰, Dˆ = 75⁰. Tính số đo của góc Bˆ?

Hướng dẫn:

Theo định lý, tổng các góc của một tứ giác bằng 360⁰.

Khi đó ta có: Aˆ + Bˆ + Cˆ + Dˆ = 360⁰.

⇔ 60⁰ + Bˆ + 150⁰ + 75⁰ = 360⁰

⇔ Bˆ = 360⁰ - 285⁰ = 75⁰.

Vậy Bˆ = 75⁰.