Với giải bài 1 trang 66 Toán lớp 8 chi tiết trong Bài 1: Tứ giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 1: Tứ giác

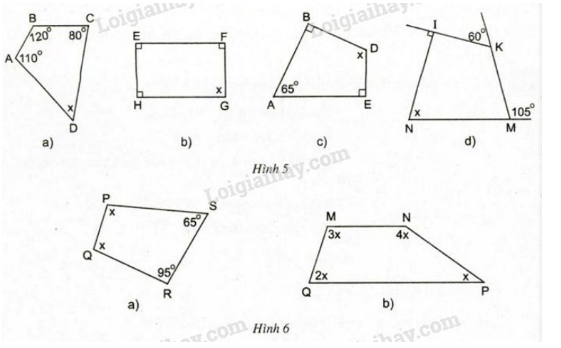
Bài 1 trang 66 sgk Toán 8 tập 1: Tìm x ở hình 5, hình 6:

Phương pháp giải: Áp dụng định lý: Tổng các góc của một tứ giác bằng ${360}^0.$

Lời giải:

Áp dụng: Tổng bốn góc trong 1 tứ giác bằng 3600

Ta có: Ở hình 5

a) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $ABCD$ ta được:

$\begin{array}{rl}& \hat{A}+\hat{B}+\hat{C}+\hat{D}={360}^0\\ & \Rightarrow \hat{D}={360}^0-\left(\hat{A}+\hat{B}+\hat{C}\right)\\ & \Rightarrow x={360}^0-\left({110}^0+{120}^0+{80}^0\right)\\ & ={360}^0-{310}^0={50}^0\end{array}$

b) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $EFGH$ ta được:

$\begin{array}{rl}& \hat{E}+\hat{F}+\hat{G}+\hat{H}={360}^0\\ & \Rightarrow \hat{G}={360}^0-\left(\hat{E}+\hat{F}+\hat{H}\right)\\ & \Rightarrow x={360}^0-\left({90}^0+{90}^0+{90}^0\right)\\ & ={360}^0-{270}^0={90}^0\end{array}$

c) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $ABDE$ ta được:

$\begin{array}{rl}& \hat{A}+\hat{B}+\hat{D}+\hat{E}={360}^0\\ & \Rightarrow \hat{D}={360}^0-\left(\hat{A}+\hat{B}+\hat{E}\right)\\ & \Rightarrow x={360}^0-\left({65}^0+{90}^0+{90}^0\right)\\ & ={360}^0-{245}^0={115}^0\end{array}$

d) Ta có: $\widehat{IKM}+{60}^0={180}^0$ (hai góc kề bù) $\Rightarrow \widehat{IKM}={180}^0-{60}^0={120}^0$

$\widehat{KMN}+{105}^0={180}^0$ (hai góc kề bù) $\Rightarrow \widehat{KMN}={180}^0-{105}^0={75}^0$

Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $MNIK$ ta được:

$\begin{array}{rl}& \widehat{KMN}+\widehat{MNI}+\widehat{NIK}+\widehat{IKM}={360}^0\\ & \Rightarrow \widehat{MNI}={360}^0-\left(\widehat{KMN}+\widehat{IKM}+\widehat{NIK}\right)\\ & \Rightarrow x={360}^0-\left({75}^0+{120}^0+{90}^0\right)\\ & ={360}^0-{285}^0={75}^0\end{array}$

Ở hình 6

a) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $PQRS$ ta được:

$\begin{array}{rl}& \hat{P}+\hat{Q}+\hat{R}+\hat{S}={360}^0\\ & \Rightarrow \hat{P}+\hat{Q}={360}^0-\left(\hat{S}+\hat{R}\right)\\ & \Rightarrow x+x={360}^0-\left({65}^0+{95}^0\right)\\ & \Rightarrow 2x={360}^0-{160}^0\\ & \Rightarrow x=\frac{{360}^0-{160}^0}{2}\\ & \Rightarrow x=\frac{{200}^0}{2}\\ & \Rightarrow x={100}^0\end{array}$

b) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $MNPQ$ ta được:

$\begin{array}{rl}& \hat{M}+\hat{N}+\hat{P}+\hat{Q}={360}^0\\ & 3x+4x+x+2x={360}^0\\ & 10x={360}^0\\ & x=\frac{{360}^0}{10}={36}^0\end{array}$

Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác: