Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Luyện tập chung trang 82 chi tiết sách Toán 7 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Luyện tập chung trang 82
Bài tập
Phương pháp giải:
-Chứng minh
Lời giải:
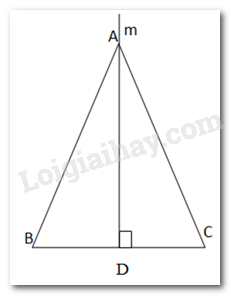
Từ A kẻ đường thẳng m vuông góc với BC tại trung điểm D của BC.
AD là đường trung tuyến của BC.
Xét và có:
(2 cạnh tương ứng)
cân tại A (đpcm).
Phương pháp giải:
-Ba đường cao trong tam giác đồng quy tại một điểm.
Lời giải:

Xét tam giác MNC có
{B}
B là trực tâm của tam giác MNC
Phương pháp giải:
-Lấy ba điểm phân biệt A, B, C trên đường viền ngoài mảnh tôn.
- Xác định giao của các đường trung trực.
Lời giải:
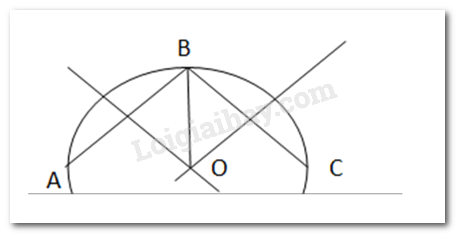
-Lấy ba điểm phân biệt A, B, C trên đường viền ngoài mảnh tôn.
- Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại O. Khi đó O là tâm cần xác định.
Phương pháp giải:
(Hai góc sole trong)
(Hai góc đồng vị)
Lời giải:
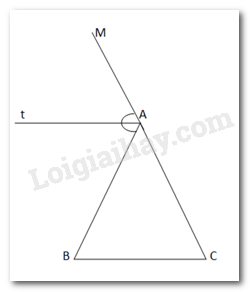
Gọi AM là tia đối của AC. At là đường phân giác của
Ta có: nên:
(Hai góc sole trong)
(Hai góc đồng vị)
Mà
Vậy tam giác ABC cân tại A ( Dấu hiệu nhận biết tam giác cân).
Bài 9.35 Trang 83 Toán lớp 7: Kí hiệu là diện tích tam giác ABC. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC.a) Chúng minh
Gợi ý: Sử dụng để chứng minh .
b) Chứng minh .
Phương pháp giải:
a)
Kẻ ,
Sử dụng để chứng minh .
b)
-Chứng minh
-Sử dụng
Lời giải:
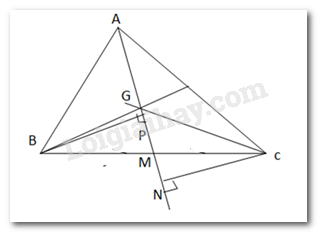
a)
Kẻ ,
Sử dụng để chứng
minh .
b)
-Chứng minh
-Sử dụng
Lời giải
a) Vì G là trọng tâm tam giác ABC nên
Kẻ ta có
(1)
Tương tự, kẻ , ta có
Cộng 2 vế của (1) và (2) ta có:
b)
Ta có
Xét và có:
BM = CM ( M là trung điểm của BC)
(2 góc đối đỉnh)
(cạnh huyền – góc nhọn)
BP = CN (cạnh tương ứng)
Ta có:
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác