Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Luyện tập chung trang 70 chi tiết sách Toán 7 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Luyện tập chung trang 70
Bài tập
Phương pháp giải:
Sử dụng định lí:
+ Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
Lời giải:
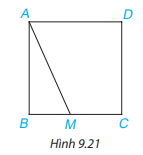
Vì ABCD là hình vuông nên BC = CD ( tính chất)
Ta coi M nằm trên cạnh BC
+) M khác B
AB là đường vuông góc kẻ từ A đến BC; AM là đường xiên kẻ từ A đến BC nên AB < AM ( đường vuông góc luôn nhỏ hơn đường xiên). Do đó, AM lớn hơn độ dài cạnh của hình vuông
+) M trùng B:
AM = AB. Do đó, AM bằng độ dài cạnh của hình vuông
Trường hợp M nằm trên cạnh CD tương tự.
Vậy độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó.
Phương pháp giải:
Kiểm tra tổng độ dài 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất không. Nếu thỏa mãn thì có tam giác có ba cạnh như vậy.
Lời giải:
Ta có: 2,5 + 3,4 = 5,9 cm < 6 cm nên không có tam giác nào với độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm.
Phương pháp giải:
+ Xét 2 trường hợp: cạnh còn lại dài 2 cm hoặc 5 cm
+ Từ bất đẳng thức tam giác, suy ra độ dài cạnh còn lại.
+ Chu vi tam giác = Tổng độ dài 3 cạnh
Lời giải:
Vì tam giác đã cho cân nên cạnh còn lại có độ dài là 2 cm hoặc 5 cm.
+) Nếu độ dài cạnh còn lại là 2 cm:
Ta có: 2 + 2 < 5 ( không thỏa mãn bất đẳng thức tam giác) (Loại).
+) Nếu độ dài cạnh còn lại là 5 cm:
2 + 5 > 5 (thỏa mãn bất đẳng thức tam giác)
Do đó, độ dài cạnh còn lại của tam giác là 5 cm.
Chu vi tam giác đó là:
2 + 5 + 5 = 12 (cm)
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh cần tìm là số tự nhiên lẻ.
Lời giải:
Gọi độ dài cạnh cần tìm là x ( cm) ( x là số tự nhiên lẻ)
Áp dụng bất đẳng thức tam giác vào tam giác đã cho, ta có:
7 – 2 < x < 7 + 2
5 < x < 9
Mà x là số tự nhiên lẻ
x = 7
Vậy độ dài cạnh còn lại của tam giác đó là 7 cm.
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)
Chu vi tam giác = Tổng độ dài 3 cạnh
Lời giải:
Gọi độ dài cạnh còn lại của tam giác là c.
Áp dụng bất đẳng thức tam giác, ta có:
a – b < c < a + b
a – b + a + b < c + a + b < a + b + a + b
2a < chu vi tam giác < 2 (a+b)
Vậy chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a+b).
Phương pháp giải:
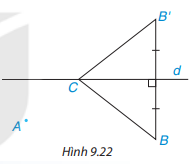
Gọi B’ là điểm sao cho d là đường trung trực của BB’.
Áp dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
Lời giải:
Gọi B’ là điểm sao cho d là đường trung trực của BB’
Khi đó, CB = CB’ ( tính chất đường trung trực của đoạn thẳng)
+) Nếu A,C,B’ không thẳng hàng thì ta lập được tam giác AB’C. Khi đó, theo bất đẳng thức tam giác, ta có:
AC + CB’ > AB’hay AC + CB > AB’, tức là độ dài đường ống dẫn nước lớn hơn độ dài AB’.
+) Nếu A,C,B’ thẳng hàng thì C nằm giữa A và B’ nên AC + CB’ = AB’, tức là độ dài đường ống dẫn nước bằng độ dài AB’.
Vậy khi đặt điểm C nằm trên bờ kênh d, sao cho A,C,B’ thẳng hàng thì tổng độ dài đường ống dẫn nước từ máy bơm đế hai khu vườn là ngắn nhất.
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 33: Quan hệ giữa ba cạnh của một tam giác
Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
Luyện tập chung trang 82
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
