Sách bài tập Toán 7 Bài 4 (Chân trời sáng tạo): Định lí và chứng minh định lí

Nguyễn Mạnh Tài Ngày: 22-09-2024 Lớp 7

2.8 K

Với giải sách bài tập Toán 7 Bài 4: Định lí và chứng minh định lí sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 4: Định lí và chứng minh định lí

Giải SBT Toán 7 trang 86 Tập 1

Bài 1 trang 86 Sách bài tập Toán 7 Tập 1: Ta gọi hai góc có tổng bằng 180° là hai góc bù nhau. Hãy viết giả thiết, kết luận bằng kí hiệu và chứng minh định lí: “Hai góc cùng bù một góc thứ ba thì hai góc đó bằng nhau”.

Lời giải

Viết giả thiết và kết luận bằng kí hiệu:

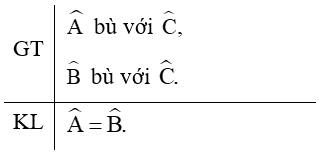
Sách bài tập Toán 7 Bài 4: Định lí và chứng minh định lí - Chân trời sáng tạo (ảnh 1)

Chứng minh định lí:

Theo GT ta có:

• $\hat{A}$ bù với $\hat{C}$ nên $\hat{A} + \hat{C} = 180 °$

Suy ra $\hat{A} = 180 ° - \hat{C}$ (1)

• $\hat{B}$ bù với $\hat{C}$ nên $\hat{B} + \hat{C} = 180 °$

Suy ra $\hat{B} = 180 ° - \hat{C}$ (2)

Từ (1) và (2) suy ra $\hat{A} = \hat{B} .$

Vậy $\hat{A} = \hat{B} .$

Bài 2 trang 86 Sách bài tập Toán 7 Tập 1: Cho định lí “Hai góc đối đỉnh thì bằng nhau”.

a) Hãy vẽ hình minh hoạ, phát biểu giả thiết của định lí trên.

b) Hãy chứng minh định lí đó.

Lời giải

a) Hình vẽ minh họa:

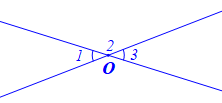
Sách bài tập Toán 7 Bài 4: Định lí và chứng minh định lí - Chân trời sáng tạo (ảnh 1)

Viết giả thiết và kết luận bằng kí hiệu:

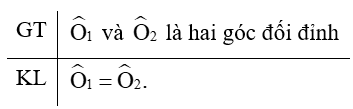
Sách bài tập Toán 7 Bài 4: Định lí và chứng minh định lí - Chân trời sáng tạo (ảnh 1)

b) Chứng minh định lí:

Ta có:

• ${\hat{O}}_{1}$ và ${\hat{O}}_{3}$ là hai góc kề bù nên

${\hat{O}}_{1} + {\hat{O}}_{3} = 180 °$

Suy ra ${\hat{O}}_{1} = 180 ° - {\hat{O}}_{3}$ (1)

• ${\hat{O}}_{2}$ và ${\hat{O}}_{3}$ là hai góc kề bù nên

${\hat{O}}_{2} + {\hat{O}}_{3} = 180 °$

Suy ra ${\hat{O}}_{2} = 180 ° - {\hat{O}}_{3}$ (2)

Từ (1) và (2) suy ra ${\hat{O}}_{1} = {\hat{O}}_{2} .$

Vậy ${\hat{O}}_{1} = {\hat{O}}_{2} .$

Bài 3 trang 86 Sách bài tập Toán 7 Tập 1: Chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.

Lời giải

Hình vẽ minh họa:

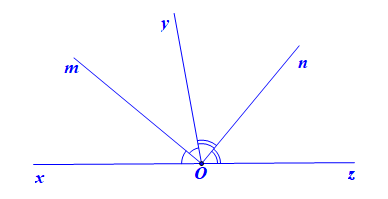
Sách bài tập Toán 7 Bài 4: Định lí và chứng minh định lí - Chân trời sáng tạo (ảnh 1)

Viết giả thiết và kết luận bằng kí hiệu:

Sách bài tập Toán 7 Bài 4: Định lí và chứng minh định lí - Chân trời sáng tạo (ảnh 1)

Chứng minh định lí:

Vì tia Om là tia phân giác của $\hat{x O y}$ nên ta có:

$\hat{x O m} = \hat{m O y} = \frac{1}{2} \hat{x O y}$ (1)

Vì tia On là tia phân giác của $\hat{y O z}$ nên ta có:

$\hat{y O n} = \hat{n O z} = \frac{1}{2} \hat{y O z}$ (2)

Từ (1) và (2) ta có:

$\hat{m O y} + \hat{y O n} = \frac{1}{2} \hat{x O y} + \frac{1}{2} \hat{y O z}$ $= \frac{1}{2} (\hat{x O y} + \hat{y O z})$

Mà $\hat{x O y}$ và $\hat{y O z}$ là hai góc kề bù nên:

$\hat{x O y} + \hat{y O z} = 180 °$

Do đó $\hat{m O y} + \hat{y O n} = \frac{1}{2} .180 ° = 90 °$

Hay $\hat{m O n} = 90 ° .$

Vậy $\hat{m O n} = 90 ° .$

Bài 4 trang 86 Sách bài tập Toán 7 Tập 1: Chứng minh định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.

Lời giải

Hình vẽ minh họa:

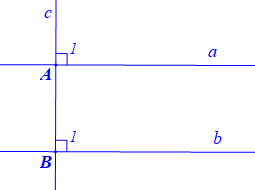
Sách bài tập Toán 7 Bài 4: Định lí và chứng minh định lí - Chân trời sáng tạo (ảnh 1)

Viết giả thiết và kết luận bằng kí hiệu:

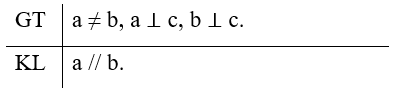
Sách bài tập Toán 7 Bài 4: Định lí và chứng minh định lí - Chân trời sáng tạo (ảnh 1)

Chứng minh định lí:

Vì a ⊥ c (GT) nên ${\hat{A}}_{1} = 90 °$

Vì b ⊥ c (GT) nên ${\hat{B}}_{1} = 90 °$

Do đó ${\hat{A}}_{1} = {\hat{B}}_{1} = 90 °$

Mà hai góc ${\hat{A}}_{1}$ và ${\hat{B}}_{1}$ ở vị trí đồng vị

Suy ra a // b.

Vậy a // b.

Bài 5 trang 86 Sách bài tập Toán 7 Tập 1: Hãy phát biểu phần kết luận còn thiếu của các định lí sau:

a) Hai góc cùng phụ một góc thứ ba thì .?.

b) Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì .?.

Lời giải

a) Hai góc cùng phụ một góc thứ ba thì bằng nhau.

b) Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.

Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Hai đường thẳng song song

Bài 4: Định lí và chứng minh định lí

Bài tập cuối chương 4

Bài 1: Thu thập và phân loại dữ liệu

Bài 2: Biểu đồ hình quạt tròn

Lý thuyết Định lí và chứng minh một định lí

1. Khái niệm định lý

Định lý là một khẳng định được suy ra từ những khẳng định được coi là đúng.

Khi định lý được phát biểu dưới dạng “Nếu … thì …”, phần nằm giữa chữ “Nếu” và chữ “thì” là phần giả thiết (viết tắt là GT), phần nằm sau chữ “thì” là phần kết luận (viết tắt là KL).

Ví dụ: Định lý: “Hai góc đối đỉnh thì bằng nhau ”

Lý thuyết Toán 7 Chân trời sáng tạo Bài 4: Định lí và chứng minh một định lí (ảnh 1)