Với giải ý b Bài 4.31 trang 65 SBT Toán lớp 10 Kết nối tri thức chi tiết trong Bài 11: Tích vô hướng của hai vectơ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải sách bài tập Toán lớp 10 Bài 11: Tích vô hướng của hai vectơ
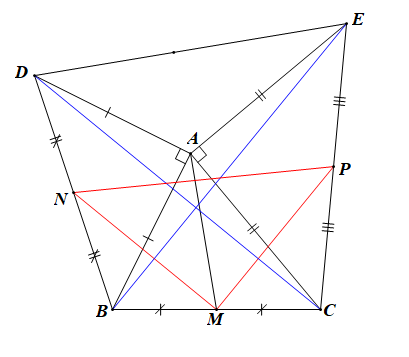
Bài 4.31 trang 65 SBT Toán 10 Tập 1: Cho tam giác ABC có Dựng ra phía ngoài tam giác hai tam giác vuông cân đỉnh A là ABD và ACE. Gọi M, N, P theo thứ tự là trung điểm BC, BD, CE. Chứng minh rằng:
b) BE vuông góc với CD;
c) Tam giác MNP là một tam giác vuông cân.
Lời giải:
b) Ta có:
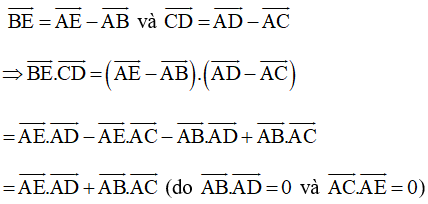
Ta có:
•
Và
• AB = AD và AC = AE
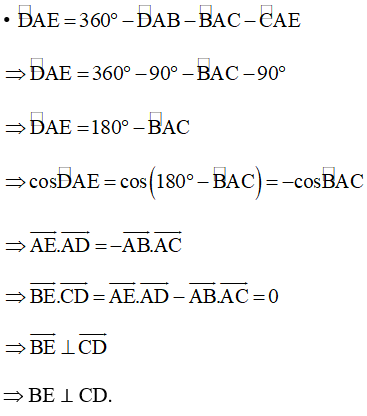
Þ BE ⊥ CD.
c) Ta có:
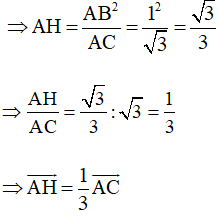
=> BE = CD (1)
Xét tam giác BCD có M, N lần lượt là trung điểm của BC, BD
Nên MN là đường trung bình của ∆BCD
và MN // CD (2)
Chứng minh tương tự ta cũng có:
MP là đường trung bình của ∆BCE
và MP // BE (3)
Từ (1), (2) và (3) suy ra MN = MP.
Vì BE ⊥ CD (câu b), MN // CD và MP // BE
Nên MN ⊥ MP
Tam giác MNP có MN = MP và
Suy ra tam giác MNP là tam giác vuông cân tại M.
Xem thêm các bài giải sách bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 4.29 trang 65 SBT Toán 10 Tập 1: Cho tam giác đều ABC có độ dài các cạnh bằng 1...
Bài 4.30 trang 65 SBT Toán 10 Tập 1: Cho hình chữ nhật ABCD có AB = 1, Gọi M là trung điểm của AD...
Bài 4.32 trang 65 SBT Toán 10 Tập 1: Cho hai vectơ và thoả mãn và ..
Bài 4.34 trang 65 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho hai điểm A(2; 1) và B(4; 3)...
Bài 4.36 trang 66 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho hai điểm A(1; 1) và B(7; 5)...
Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 10: Vectơ trong mặt phẳng tọa độ
Bài 11: Tích vô hướng của hai vectơ
Bài 13: Các số đặc trưng đo xu thế trung tâm
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
