Với giải Bài 8 trang 88 Toán 12 Tập 2 Cánh diều chi tiết trong Bài tập cuối chương 5 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài tập cuối chương 5

Bài 8 trang 88 Toán 12 Tập 2: Xác định vị trí tương đối của hai đường thẳng ∆₁ và ∆₂ trong mỗi trường hợp sau:

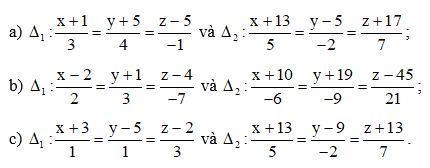
Lời giải:

a) Đường thẳng ∆₁ đi qua điểm M₁(– 1; – 5; 5) và có $\overrightarrow{u_1}=\left(3;4;-1\right)$ là vectơ chỉ phương.

Đường thẳng ∆₂ đi qua điểm M₂(– 13; 5; – 17) và có $\overrightarrow{u_2}=\left(5;-2;7\right)$ là vectơ chỉ phương.

Ta có $\frac{3}{5}\ne \frac{4}{-2}$, suy ra hai vectơ $\overrightarrow{u_1},\overrightarrow{u_2}$ không cùng phương.

$\overrightarrow{M_1{M}_2}=\left(-12;10;-22\right)$, $\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]=\left(\left|\begin{array}{cc}4& -1\\ -2& 7\end{array}\right|;\left|\begin{array}{cc}-1& 3\\ 7& 5\end{array}\right|;\left|\begin{array}{cc}3& 4\\ 5& -2\end{array}\right|\right)=\left(26;-26;-26\right)$.

Do $\left[\overrightarrow{u_1}\cdot \overrightarrow{u_2}\right]\cdot \overrightarrow{M_1{M}_2}=$ 26 ∙ (– 12) + (– 26) ∙ 10 + (– 26) ∙ (– 22) = 0 nên $\overrightarrow{u_1},\overrightarrow{u_2},\overrightarrow{M_1{M}_2}$ đồng phẳng.

Vậy ∆₁ cắt ∆₂.

b) Đường thẳng ∆₁ đi qua điểm M₁(2; – 1; 4) và có $\overrightarrow{u_1}=\left(2;3;-7\right)$ là vectơ chỉ phương.

Đường thẳng ∆₂ đi qua điểm M₂(– 10; – 19; 45) và có $\overrightarrow{u_2}=\left(-6;-9;21\right)$ là vectơ chỉ phương.

Ta có $\overrightarrow{u_2}=-3\overrightarrow{u_1}$, suy ra hai vectơ $\overrightarrow{u_1},\overrightarrow{u_2}$ cùng phương.

$\overrightarrow{M_1{M}_2}=\left(-12;-18;41\right)$ và $\frac{-12}{2}=\frac{-18}{3}\ne \frac{41}{-7}$ nên $\overrightarrow{u_1},\overrightarrow{M_1{M}_2}$ không cùng phương.

Vậy ∆₁ // ∆₂.

c) Đường thẳng ∆₁ đi qua điểm M₁(– 3; 5; 2) và có $\overrightarrow{u_1}=\left(1;1;3\right)$ là vectơ chỉ phương.

Đường thẳng ∆₂ đi qua điểm M₂(– 13; 9; – 13) và có $\overrightarrow{u_2}=\left(5;-2;7\right)$ là vectơ chỉ phương.

Ta có $\frac{1}{5}\ne \frac{1}{-2}$, suy ra hai vectơ $\overrightarrow{u_1},\overrightarrow{u_2}$ không cùng phương.

$\overrightarrow{M_1{M}_2}=\left(-10;4;-15\right)$, $\left[\overrightarrow{u_1},\overrightarrow{u_2}\right]=\left(\left|\begin{array}{cc}1& 3\\ -2& 7\end{array}\right|;\left|\begin{array}{cc}3& 1\\ 7& 5\end{array}\right|;\left|\begin{array}{cc}1& 1\\ 5& -2\end{array}\right|\right)=\left(13;8;-7\right)$.

Do $\left[\overrightarrow{u_1}\cdot \overrightarrow{u_2}\right]\cdot \overrightarrow{M_1{M}_2}=$13 ∙ (– 10) + 8 ∙ 4 + (– 7) ∙ (– 15) = 7 ≠ 0 nên $\overrightarrow{u_1},\overrightarrow{u_2},\overrightarrow{M_1{M}_2}$ không đồng phẳng.

Vậy ∆₁ và ∆₂ chéo nhau.