Với giải Bài 2 trang 74 Toán 9 Tập 2 Chân trời sáng tạo chi tiết trong Bài 2: Tứ giác nội tiếp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Tứ giác nội tiếp

Bài 2 trang 74 Toán 9 Tập 2: Cho tam giác nhọn ABC. Gọi A', B', C' lần lượt là chân đường cao kẻ từ A, B, C và H là trực tâm của tam giác đó. Hãy chỉ ra các tứ giác nội tiếp có trong hình.

Lời giải:

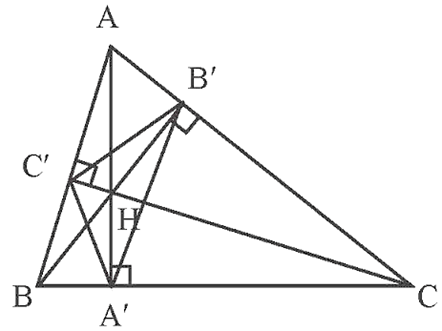
Ta có ∆AB'H vuông tại B' và ∆AC'H vuông tại C' cùng nội tiếp đường tròn đường kính AH.

Suy ra tứ giác AB'HC' nội tiếp đường tròn đường kính AH.

Tương tự, ta có tứ giác BA'HC' nội tiếp đường tròn đường kính BH và tứ giác CA'HC' nội tiếp đường tròn đường kính BH và tứ giác CA'HB' nội tiếp đường tròn đường kính CH.

Ta lại có ∆AB'B vuông tại B' và ∆AA'B vuông tại A' cùng nội tiếp đường tròn đường kính AB.

Suy ra tứ giác AB'A'B nội tiếp đường tròn đường kính AB.

Tương tự, ta có tứ giác BC'B'C nội tiếp đường tròn đường kính BC và tứ giác AC'A'C nội tiếp đường tròn đường kính BH và tứ giác CA'HB' nội tiếp đường tròn đường kính AC.