Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 3: Đa giác đều và phép quay chi tiết sách Toán 9 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 3: Đa giác đều và phép quay

Khởi động trang 75 Toán 9 Tập 2:

− Độ dài các đoạn thẳng;

− Góc hợp bởi hai đoạn thẳng liên tiếp.

Lời giải:

Trong mỗi hình, độ dài các đoạn thẳng bằng nhau, độ lớn các góc hợp bởi hai đoạn thẳng liên tiếp bằng nhau.

1. Khái niệm đa giác đều

Khám phá 1 trang 75 Toán 9 Tập 2: Có nhận xét gì về cạnh và góc của mỗi đa giác sau?

Lời giải:

Trong Hình 2, ta thấy:

− Độ dài các cạnh của mỗi đa giác là bằng nhau.

− Số đo góc của mỗi đa giác là bằng nhau.

Thực hành 1 trang 77 Toán 9 Tập 2: Cho đường tròn (O; R), trên đó lấy các điểm M, N, P, Q, R sao cho số đo các cung $\stackrel{⏜}{MN},\stackrel{⏜}{NP},\stackrel{⏜}{PQ},\text{\hspace{0.17em}\hspace{0.17em}}\stackrel{⏜}{QR},\stackrel{⏜}{RM}$ bằng nhau. Đa giác MNPQR có là đa giác đều không? Vì sao?

Lời giải:

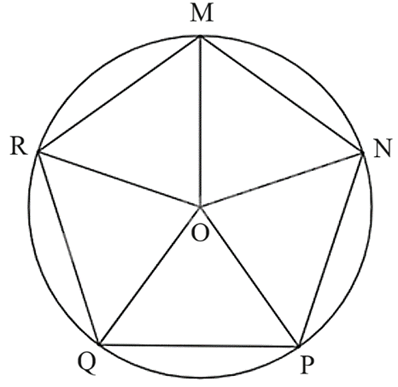
Các cung $\stackrel{⏜}{MN},\stackrel{⏜}{NP},\stackrel{⏜}{PQ},\text{\hspace{0.17em}\hspace{0.17em}}\stackrel{⏜}{QR},\stackrel{⏜}{RM}$ chia đường tròn (O; R) thành 6 cung có số đo bằng nhau, suy ra số đo mỗi cung là 360° : 5 = 72°.

Ta có $\widehat{MON}$ là góc nội tiếp chắn cung MN suy ra $\widehat{MON}$ = 72^o.

Xét ΔMON, có: OM = ON = R suy ra ΔMON cân tại O.

Suy ra $\widehat{OMN}=\widehat{ONM}$ (tính chất tam giác cân).

Do đó $\widehat{OMN}=\widehat{ONM}=\frac{180°-\widehat{MON}}{2}=54°.$

Tương tự, ta có $\widehat{OPN}=\widehat{ONP}=54°.$

Suy ra $\widehat{MPN}=\widehat{OPN}+\widehat{ONP}=54°+54°=108°.$

Xét ΔOMN và ΔONP có:

$\widehat{MON}=\widehat{NOP};$ OM = OP; ON chung.

Do đó ΔOMN = ΔONP (c.g.c).

Suy ra MN = NP (hai cạnh tương ứng).

Chứng minh tương tự, ta thu được ngũ giác MNPQR có các cạnh bằng nhau và các góc đều bằng nhau (đều bằng 108°).

Vậy MNPQR là một đa giác đều.

Vận dụng 1 trang 77 Toán 9 Tập 2: Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA. Đa giác MNPQRS có là đa giác đều không? Vì sao?

Lời giải:

Do ABCDEF là lục giác đều nên

• $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=\widehat{E}=\widehat{F}=120°$.

• AB = BC = CD = DE = EF = FA.

Vì M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA.

Suy ra AM = MB = BN = NC = CP = PD = DQ = QE = ER = RF = FS = SA.

Xét ΔSAM và ΔMBN có:

$\widehat{A}=\widehat{B}$ (chứng minh trên);

AM = BN (chứng minh trên);

SA = MB (chứng minh trên).

Do đó ΔSAM = ΔMBN  (c.g.c).

Suy ra SM = MN (hai cạnh tương ứng).

Chứng minh tương tự ta được: MN = NP, NP = PQ, QR = RS, RS = SM.          (1)

Vì AS = AM (chứng minh trên) suy ra ΔASM cân tại A.

Suy ra $\widehat{\text{AS}M}=\widehat{\text{ASM}}$ (tính chất tam giác cân).

Do đó $\widehat{\text{AS}M}=\widehat{\text{ASM}}=\frac{180°-\widehat{A}}{2}=30°$ (tổng 3 góc trong của tam giác).

Tương tự ta thu được:

• $\widehat{BMN}=\widehat{\text{BNM}}=\frac{180°-\widehat{B}}{2}=30°$;

• $\widehat{CNP}=\widehat{CPN}=\frac{180°-\widehat{C}}{2}=30°$;

• $\widehat{DPQ}=\widehat{DQP}=\frac{180°-\widehat{D}}{2}=30°$;

• $\widehat{EQR}=\widehat{\text{ER}Q}=\frac{180°-\widehat{E}}{2}=30°$;

• $\widehat{FRS}=\widehat{FSR}=\frac{180°-\widehat{F}}{2}=30°$.

Ta có $\widehat{RSM}=180°-\widehat{FSR}-\widehat{ASM}=180°-30°-30°=120°.$

Tương tự, ta được: $\widehat{AMN}=\widehat{MNP}=\widehat{NQP}=\widehat{PQR}=\widehat{QRS}=120°.$ (2)

Từ (1) và (2), suy ra MNPQRS là đa giác đều.

2. Phép quay

Khám phá 2 trang 77 Toán 9 Tập 2: Vẽ hình vuông ABCD tâm O (Hình 5a). Cắt một tấm bìa hình vuông (gọi là ℋ) cùng độ dài cạnh với hình vuông ABCD (Hình 5b). Đặt hình vuông ℋ trùng khít lên hình vuông ABCD sao cho tại đỉnh M của H trùng với điểm A, rồi dùng đinh ghim cố định tâm của ℋ tại tâm O của hình vuông ABCD (Hình 5c). Quay hình vuông ℋ quanh điểm O ngược chiều kim đồng hồ cho đến khi đỉnh M của ℋ trùng lại với đỉnh A (Hình 5d).

a) Khi điểm M trùng với B thì M vạch lên một cung tròn có số đo bằng bao nhiêu?

b) Trong quá trình trên, hình vuông ℋ trùng khít với hình vuông ABCD bao nhiêu lần (không tính vị trí ban đầu trước khi quay)? Ứng với mỗi lần đó, điểm M vạch nên cung có số đo bao nhiêu?

Lời giải:

a) Khi điểm M trùng với B thì M vạch lên một cung tròn có số đo bằng 270°.

b) Trong quá trình trên, hình vuông H trùng khít với hình vuông ABCD 4 lần (không tính vị trí ban đầu trước khi quay).

• Lần 1, điểm M vạch lên cung số đo 90°.

• Lần 2, điểm M vạch lên cung số đo 180°.

• Lần 3, điểm M vạch lên cung số đo 270°.

• Lần 4, điểm M vạch lên cung số đo 360°.

Thực hành 2 trang 78 Toán 9 Tập 2: Tìm phép quay biến hình ngũ giác đều tâm I thành chính nó (Hình 8).

Lời giải:

Ta có I đỉnh của ngũ giác đều chia đường tròn (I) thành 5 cung bằng nhau, mỗi cung đo có số đo 72°.

Do đó, các phép quay 72°, 144°, 216°, 288° hoặc 360° tâm I cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ biến ngũ giác đều tâm I thành chính nó.

Vận dụng 2 trang 78 Toán 9 Tập 2: Một vòng quay may mắn có dạng hình đa giác đều 10 cạnh (Hình 9). Tìm các phép quay biến đa giác này thành chính nó.

Lời giải:

Gọi O là tâm đối xứng của đa giác đều 10 cạnh.

Ta có 10 đỉnh của đa giác đều, 10 cạnh chia đường tròn thành 10 cung bằng nhau mỗi cung có số đo 36°.

Do đó, các phép quay 36°, 72°, 108°, 144°, 180°, 216°, 252°, 288°, 324° hoặc 360°; tâm O cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ biến đa giác đều 10 cạnh thành chính nó.

3. Hình phẳng đều trong thực tế

Thực hành 3 trang 79 Toán 9 Tập 2: Em hãy tìm một số hình phẳng đều trong thực tế.

Lời giải:

Hình phẳng đều trong thực tế: mỗi mặt của rubik, bàn cờ, hộp mứt tết, viên gạch trang trí, biển báo giao thông,...

Bài tập

Bài 1 trang 79 Toán 9 Tập 2: Gọi tên đa giác đều trong mỗi hình sau và tìm các phép quay có thể biến mỗi hình dưới đây thành chính nó.

Lời giải:

• Hình 11a) là tam giác đều.

Các phép quay biến tam giác đều thành chính nó là các phép quay 120°, 240° hoặc 360° tâm O cùng chiều hay ngược chiều kim đồng hồ.

• Hình 11b) là hình vuông.

Các phép quay biến hình vuông thành chính nó là các phép quay 90°, 180°, 270°, 360° tâm I cùng chiều hay ngược chiều kim đồng hồ.

• Hình 11c) là ngũ giác đều.

Các phép quay biến ngũ giác đều thành chính nó là các phép quay 72°, 144°, 216°, 288°, 360° tâm A cùng chiều hay ngược chiều kim đồng hồ.

• Hình 11d) là lục giác đều.

Các phép quay biến lục giác đều thành chính nó là các phép quay 60°, 120°, 180°, 240°, 300°, 360° tâm B cùng chiều hay ngược chiều kim đồng hồ.

• Hình11 e) là bát giác đều.

Các phép quay biến bát giác đều thành chính nó là các phép quay 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360° tâm C cùng chiều hay ngược chiều kim đồng hồ.

Bài 2 trang 79 Toán 9 Tập 2: Cho đa giác đều 9 cạnh có tâm O và AB, BC là hai cạnh đa giác (Hình 12).

a) Tìm số đo các góc $\widehat{AOB},\widehat{ABO},\widehat{ABC}.$

b) Tìm các phép quay biến đa giác thành chính nó.

Lời giải:

a) Ta có 9 đỉnh của đa giác chia đường tròn thành 9 phần bằng nhau, số đo mỗi cung là:

360° : 9 = 40°.

Vì $\widehat{AOB}$ là góc nội tiếp chắn cung AB nhỏ nên $\widehat{AOB}=40°.$

Do OA = OB = R nên tam giác AOB cân tại O

Suy ra $\widehat{OAB}=\widehat{OBA}=\frac{180°-\widehat{AOB}}{2}=70°.$

Tương tự, ta có $\widehat{COB}=40°.$

Suy ra $\widehat{OBC}=\widehat{OCB}=\frac{180°-\widehat{BOC}}{2}=70°.$

Ta có $\widehat{ABC}=\widehat{OBA}+\widehat{OBC}=70°+70°=140°.$

b) Các phép quay 40°, 80°, 120°, 160°, 200°, 240°, 280°, 320° hoặc 360° tâm O cùng chiều hay ngược chiều kim đồng hồ biến đa giác thành chính nó.

Bài 3 trang 80 Toán 9 Tập 2: Đường viền ngoài của chiếc đồng hồ trong Hình 13 được làm theo hình đa giác đều nào? Tìm phép quay biến đa giác này thành chính nó.

Lời giải:

Đường viền ngoài của chiếc đồng hồ trong Hình 13 được làm theo hình bát giác đều.

Ta có 8 đỉnh của đa giác được chia thành 8 phần bằng nhau, mỗi cung có số đo 45°.

Do đó, các phép quay biến bát giác đều thành chính nó là 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360° theo chiều hoặc ngược chiều kim đồng hồ.

Bài 4 trang 80 Toán 9 Tập 2: Cho đường tròn (O; R).

a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên (O; R).

b) Tính các cạnh của các hình vừa vẽ theo R.

Lời giải:

a) Hình tam giác đều GHK, hình vuông MNPQ, hình lục giác đều ABCDEF có các đỉnh nằm trên (O; R) được vẽ như hình dưới đây.

b) • Xét tam giác đều GHK.

Kẻ đường cao GI (I ∈ HK). Xét tam giác GIK vuông tại I, ta có:

GI = $\frac{3}{2}$GO = $\frac{3}{2}$R;

GI = GK . sin K, suy ra $GK=\frac{GI}{\sin K}=\frac{\frac{3}{2}R}{\frac{\sqrt{3}}{2}}=R\sqrt{3}.$

• Xét hình vuông MNPQ.

Tam giác NOP vuông tại O.

Theo định lí Pythagore, ta có: NP² = ON² + OP² = R² + R² = 2R².

Suy ra NP = R$\sqrt{2}$.

 • Xét hình lục giác đều ABCDEF.

Tam giác AOB có OA = OB và $\widehat{AOB}=\frac{360°}{6}=60°$ nên là tam giác AOB đều.

Suy ra AB = OA = OB = R.

Vậy cạnh của tam giác đều GHK là R$\sqrt{3}$, cạnh hình vuông MNPQ là R$\sqrt{2}$ và cạnh hình lục giác đều ABCDEF là R.

Bài 5 trang 80 Toán 9 Tập 2: Tìm các hình phẳng có tính đều:

a) Trong tự nhiên;

b) Trong sản xuất, thiết kế, mĩ thuật.

Lời giải:

a) Các hình phẳng có tính đều trong tự nhiên như con sao biển, bông hoa, lát cam,...

b) Các hình phẳng có tính đều trong sản xuất, thiết kế, mĩ thuật: trang trí nội thất, gạch,...

Bài 6 trang 80 Toán 9 Tập 2: Vòng trong của mái giếng trời hình hoa sen của nhà ga Bến Thành (Thành phố Hồ Chí Minh) có dạng đa giác đều 12 cạnh (Hình 14).

Hãy chỉ ra các phép quay biến đa giác đều thành chính nó.

Lời giải:

Ta có 12 đỉnh của đa giác chia  đường tròn thành 12 phần bằng nhau. Số đo mỗi cung là 30°.

Do đó, các phép quay biến đa giác này thành chính nó là các phép quay 30°, 60°, 90°, 120°, 150°, 180°, 210°, 240°, 270°, 300°, 330° hoặc 360° theo chiều kim đồng hồ hay ngược chiều kim đồng hồ.

Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Bài 2. Tứ giác nội tiếp

Bài 3. Đa giác đều và phép quay

Bài tập cuối chương 9

Bài 1. Hình trụ

Bài 2. Hình nón

Bài 3. Hình cầu

Lý thuyết Đa giác đều và phép quay

1. Khái niệm đa giác đều

− Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau được gọi là đa giác đều.

Chú ý:

− Đa giác đều có số cạnh bằng n được gọi là n-giác đều.

− Với n lần lượt bằng 3, 4, 5, 6, 8 … ta có tam giác đều, tứ giác đều (hình vuông), ngũ giác đều, lục giác đều, bát giác đều,…

− Khi nói đến đa giác đều mà không chú thích gì thêm, ta hiểu đó là đa giác lồi.

− Người ta chứng minh được, với mỗi đa giác đều có đúng một điểm I cách đều tất cả các đỉnh của đa giác. Điểm I gọi là tâm của đa giác đó.

Ví dụ: Dưới đây là một số đa giác đều thường gặp:

2. Phép quay

− Phép quay thuận chiều α° (0° < α° < 360°) tâm O giữ nguyên điểm O, biến điểm M khác điểm O thành điểm M' thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM' thì điểm M tạo nên cung MM' có số đo α°.

− Định nghĩa tương tự cho phép quay ngược chiều α° tâm O.

− Phép quay 0° hay 360° giữ nguyên mọi điềm.

Chú ý:

−  Ta coi mỗi phép quay tâm O biến O thành chính nó.

− Nếu một phép quay biến các điểm M trên hình a thành các điểm M' thì các điểm M' tạo thành hình a'. Khi đó, ta nói phép quay biến hình a thành hình a'. Nếu hình a' trùng với hình a thì ta nói phép quay biến hình a thành chính nó.

Ví dụ: Cho tam giác đều ABC tâm O như hình dưới đây:

Phép quay biến điểm A thành điểm C sẽ biến các điểm C, B tương ứng thành các điểm B, A như hình dưới đây:

Đây là phép quay thuận chiều 120° tâm O hoặc phép quay ngược chiều 240° tâm O.

3. Hình phẳng đều trong thực tế

− Tương tự như các đa giác đều, trong tự nhiên, sản xuất, thiết kế, … cũng có các hình phẳng đều.

Ví dụ: Dưới đây là một số đa giác đều trong thực tế: