Với tóm tắt lý thuyết Toán lớp 9 Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.
Lý thuyết Toán 9 Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn
A. Lý thuyết Đường tròn. Vị trí tương đối của hai đường tròn
1. Khái niệm đường tròn
|
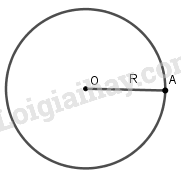
Trong mặt phẳng, đường tròn tâm O bán kính R là tập hợp các điểm cách điểm O một khoảng bằng R (R > 0), kí hiệu là (O;R). |
Chú ý:
- Một đường tròn hoàn toàn xác định khi biết tâm và bán kính.
- Khi không quan tâm đến bán kính của đường tròn (O;R), ta cũng có thể kí hiệu đường tròn là (O).
Vị trí tương đối của điểm và đường tròn
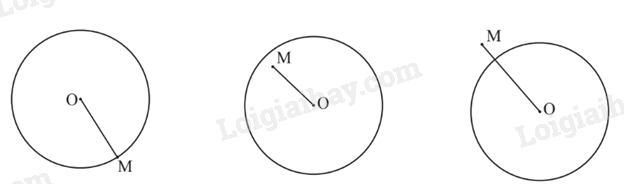
Cho đường tròn (O; R) và điểm M. Khi đó:
- Nếu điểm M thuộc đường tròn (O) (hay ta còn nói điểm M nằm trên đường tròn (O), hoặc đường tròn (O) đi qua điểm M) thì OM = R và ngược lại.
- Nếu điểm M nằm bên trong (hay nằm trong, ở trong) đường tròn (O) thì OM < R và ngược lại.
- Nếu điểm M nằm bên ngoài (hay nằm ngoài, ở ngoài) đường tròn (O) thì OM > R và ngược lại.
2. Liên hệ giữa đường kính và dây của đường tròn
Chú ý:
- Đoạn thẳng nối hai điểm phân biệt thuộc đường tròn được gọi là dây (hay dây cung) của đường tròn.
- Dây đi qua tâm là đường kính của đường tròn. Trong các dây của đường tròn, dây lớn nhất là đường kính.
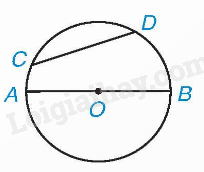
Ví dụ: Cho hai điểm C, D cùng thuộc một đường tròn. Đoạn thẳng CD gọi là dây cung hoặc dây. Đường kính AB là một dây đi qua tâm.
3. Tính đối xứng của đường tròn
Nhận xét: Điểm đối xứng của một điểm tùy ý trên đường tròn qua tâm của đường tròn cũng nằm trên đường tròn đó.
|
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó. |
Nhận xét: Điểm đối xứng của một điểm tùy ý trên đường tròn qua một đường thẳng đi qua tâm của đường tròn cũng nằm trên đường tròn đó.
|
Đường tròn là hình có trục đối xứng. Mỗi đường thẳng đi qua tâm là một trục đối xứng của đường tròn đó. |
Ví dụ:
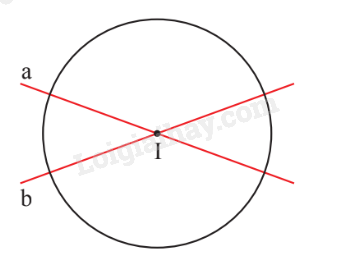
Hình tròn tâm I có:
I là tâm đối xứng;
Đường thẳng a, b là các trục đối xứng của hình tròn (I).
4. Vị trí tương đối của hai đường tròn
Hai đường tròn cắt nhau
|
Hai đường tròn có đúng hai điểm chung gọi là hai đường tròn cắt nhau.
|
Mỗi điểm chung của hai đường tròn cắt nhau được gọi là một giao điểm của hai đường tròn đó.
Nếu hai đường tròn (O;R) và (O’;r) với cắt nhau thì .
Hai đường tròn tiếp xúc nhau
|
Hai đường tròn có đúng một điểm chung gọi là hai đường tròn tiếp xúc nhau (tại điểm chung đó). |
Điểm chung của hai đường tròn tiếp xúc nhau được gọi là tiếp điểm.
Có hai trường hợp về hai đường tròn tiếp xúc nhau:
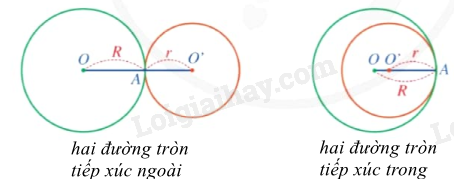
Nếu hai đường tròn (O;R) và (O’;r) tiếp xúc ngoài thì tiếp điểm A nằm giữa O, O’ và . Điều ngược lại cũng đúng.
Với R > r, nếu hai đường tròn (O;R) và (O’;r) tiếp xúc trong thì điểm O’ nằm giữa O, A và . Điều ngược lại cũng đúng.
Hai đường tròn không giao nhau
|
Hai đường tròn không có điểm chung gọi là hai đường tròn không giao nhau. |
Có hai trường hợp về hai đường tròn không giao nhau:
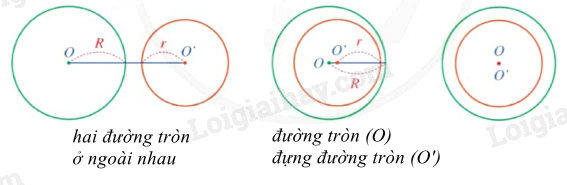
Nếu hai đường tròn (O;R) và (O’;r) ở ngoài nhau thì . Điều ngược lại cũng đúng.
Với R > r, nếu đường tròn (O) đựng đường tròn (O’) thì . Điều ngược lại cũng đúng.
Nhận xét: Ta có thể nhận biết vị trí tương đối của hai đường tròn thông qua hệ thức liên hệ giữa OO’ với R và r được tóm tắt trong bảng sau:
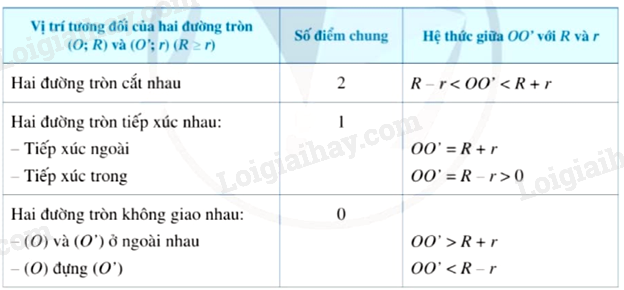
Ví dụ 1: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:
4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.
Ví dụ 2: Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.
Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.
Ví dụ 3: Cho đường tròn (O;3cm) và (O’;4cm) có thì nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.
Sơ đồ tư duy Đường tròn. Vị trí tương đối của hai đường tròn

B. Bài tập Đường tròn. Vị trí tương đối của hai đường tròn
Bài 1. Cho đường tròn (O; 5 cm) và hai điểm A, B. Biết rằng cm và OB = 5 cm. Khi đó:
A. Điểm A nằm trong (O), điểm B nằm trên (O);
B. Điểm A nằm trên (O), điểm B nằm trong (O);
C. Điểm A nằm ngoài (O), điểm B nằm trên (O);
D. Điểm A nằm trong (O), điểm B nằm ngoài (O).
Hướng dẫn giải
Đáp án đúng là: A
Đường tròn (O) có bán kính R = 5 cm.
Vì cm < 5 cm nên OA < R, do đó điểm A nằm trong đường tròn (O).
Vì OB = R = 5 cm nên điểm B nằm trên đường tròn (O).
Vậy ta chọn phương án A.
Bài 2. Đường tròn có bao nhiêu trục đối xứng?
A. 1;
B. 2;
C. 3;
D. Vô số.
Hướng dẫn giải
Đáp án đúng là: D
Mỗi đường thẳng đi qua tâm của đường tròn là một trục đối xứng của đường tròn đó.
Vậy đường tròn có vô số trục đối xứng.
Bài 3. Cho hai đường tròn (O; 9 cm), (O’; 8 cm) với OO’ = 17 cm. Kết luận nào sau đây đúng về vị trí tương đối của hai đường tròn?
A. Hai đường tròn ở ngoài nhau;
B. Hai đường tròn tiếp xúc ngoài;
C. Hai đường tròn tiếp xúc trong;
D. Hai đường tròn cắt nhau.
Hướng dẫn giải
Đáp án đúng là: B
Ta thấy bán kính của hai đường tròn (O), (O’) lần lượt là R = 9 cm và r = 8 cm.
Vì R + r = 9 + 8 = 17 (cm) nên OO’ = R + r.
Vậy hai đường tròn đã cho tiếp xúc ngoài.
Bài 4. Cho đường tròn (O), đường kính BC. Chứng minh rằng với điểm A bất kì (khác B và C) nằm trên đường tròn (O), ta đều có BC < AB + AC < 2BC.
Hướng dẫn giải
Áp dụng bất đẳng thức tam giác cho tam giác ABC, ta có: BC < AB + AC (1)
Đường tròn (O), có: AB là dây cung, BC là đường kính nên AB < BC.
Chứng minh tương tự, ta được AC < BC.
Khi đó AB + AC < BC + BC = 2BC (2)
Từ (1), (2), ta có: BC < AB + AC < 2BC.
Bài 5. Cho đường tròn (O; R), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d; C và D lần lượt là điểm đối xứng với A và B qua O.
a) Ba điểm B, C và D có thuộc (O) không? Vì sao?
b) Chứng minh rằng AB // CD.
c) Chứng minh rằng C và D đối xứng với nhau qua d.
Hướng dẫn giải
a) ⦁Ta có B là điểm đối xứng với A thuộc (O) qua d, mà d đi qua O nên điểm B cũng nằm trên (O).
⦁Ta có C là điểm đối xứng với A thuộc (O) qua O nên C thuộc (O).
⦁Ta có D là điểm đối xứng với Bthuộc (O) qua O nên C thuộc (O).
Vậy ba điểm B, C và D thuộc (O).
b) Xét ∆OAB và ∆OCD, có:
OA = OC = R (do A, C cùng thuộc (O));
OB = OD = R (do B, D cùng thuộc (O));
(đối đỉnh).
Do đó ∆OAB = ∆OCD (c.g.c).
Suy ra (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AB // CD.
c) Ta có AB // CD (câu b) và d ⊥ AB (do A và B đối xứng với nhau qua d) nên d ⊥ CD.
Tam giác OCD cân tại O (do OC = OD = R) có d là đường cao nên d cũng là đường trung trực của tam giác OCD.
Vậy C và D đối xứng với nhau qua d.
Bài 6. Xác định vị trí tương đối của hai đường tròn (O; R) và (O’; R’) trong mỗi trường hợp sau:
a) OO’ = 20; R = 8; R’ = 4.
b) OO’ = 15; R = 8; R’ = 7.
c) OO’ = 6; R = 9; R’ = 4.
d) OO’ = 1; R = 7; R’ = 5.
e) OO’ = 4; R = 6;R’ = 2.
Hướng dẫn giải
a) Ta thấy: R + R’ = 8 + 4 < 20 nên R + R’ < OO’.
Vậy hai đường tròn (O; R) và (O’; R’) ở ngoài nhau.
b) Ta thấy: R + R’ = 8 + 7 = 15 nên R + R’ = OO’.
Vậy hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài.
c) Ta thấy: 9 – 4 < 6 < 9 + 4 nên R – R’ < OO’ < R + R’.
Vậy hai đường tròn (O; R) và (O’; R’) cắt nhau.
d) Ta thấy: R – R’ = 7 – 5 > 1 nên R – R’ > OO’.
Vậy đường tròn (O; R) đựng đường tròn (O’; R’).
e) Ta thấy: R – R’ = 6 – 2 = 4 nên R – R’ = OO’.
Vậy hai đường tròn đã cho tiếp xúc trong với nhau.
Bài 7. Mô tả vị trí tương đối giữa mỗi cặp đường viền cồng chiêng trong hình chụp bộ cồng chiêng Tây Nguyên ở hình dưới đây.
Hướng dẫn giải
Cặp đường tròn mô tảđường viền ở cặp cồng chiêng trong Hình a) không có điểm chung nên cặp đường tròn này không giao nhau.
Cặp đường tròn mô tảđường viền ở cặp cồng chiêng trong Hình b) có một điểm chung và không có cồng chiêng nào treo trước cồng chiêng còn lại nên cặp đường tròn này tiếp xúc ngoài với nhau.
Cặp đường tròn mô tả đường viền ở cặp cồng chiêng trong Hình c) có hai điểm chung nên cặp đường tròn này cắt nhau tại hai điểm phân biệt.
Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn
Lý thuyết Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn
Lý thuyết Bài 2: Vị trí tương đối của đường thẳng và đường tròn
Lý thuyết Bài 3: Tiếp tuyến của đường tròn
Lý thuyết Bài 4: Góc ở tâm. Góc nội tiếp
Lý thuyết Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên