Với tóm tắt lý thuyết Toán lớp 9 Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

A. Lý thuyết Một số hệ thức về cạnh và góc trong tam giác vuông

1. Tính cạnh góc vuông theo cạnh huyền và tỉ số lượng giác của góc nhọn

Ví dụ 1:

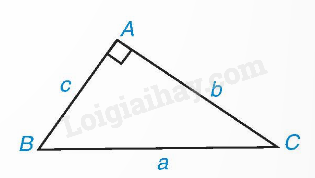
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=a.\sin B=a.\cos C;\\ c=a.\sin C=a.\cos B.\end{array}$

2. Tính cạnh góc vuông theo cạnh góc vuông còn lại và tỉ số lượng giác của góc nhọn

Ví dụ 2:

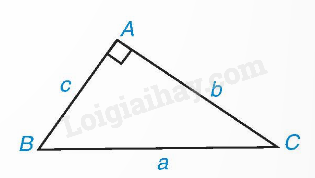
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=c.\tan B=c.\cot C;\\ c=b.\tan C=b.\cot B.\end{array}$

3. Áp dụng tỉ số lượng giác của góc nhọn để giải tam giác vuông

Giải tam giác vuông là tìm tất cả độ dài các cạnh và số đo các góc còn lại của tam giác đó.

Sơ đồ tư duy Một số hệ thức về cạnh và góc trong tam giác vuông

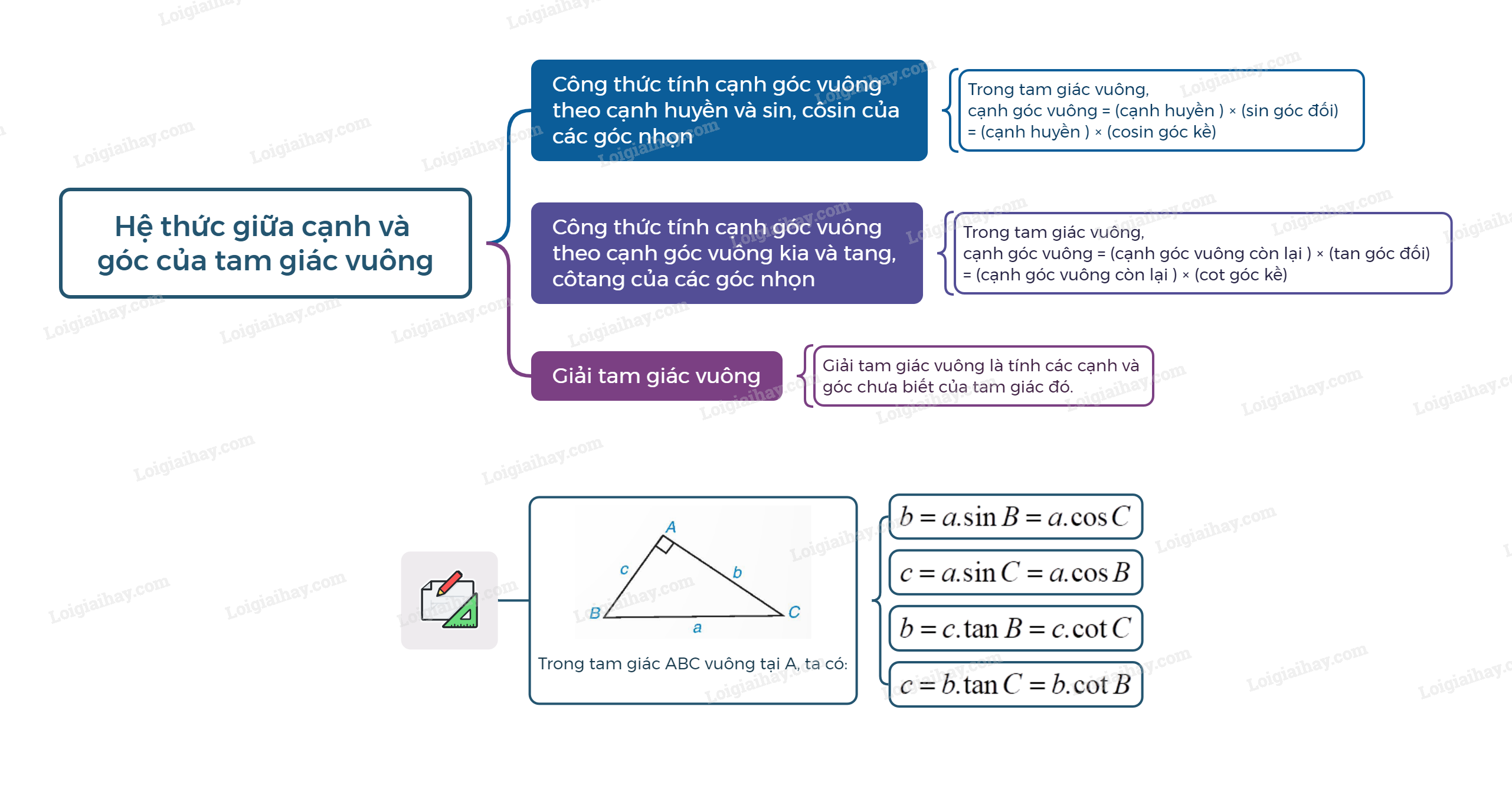
B. Bài tập Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 1. Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?

A. MN = MP.sinP;

B. MN = MP.cosP;

C. MN = MP.tanP;

D. MN = MP.cotP.

Hướng dẫn giải

Đáp án đúng là: A

Tam giác MNP vuông tại N nên MN = MP.sinP.

Bài 2. Cho tam giác ABC vuông tại A có AC = 20 cm, $\hat{C}=60°$. Độ dài các cạnh AB, BC lần lượt là

A. $20\sqrt{3}$cm và 40 cm;

B. $20\sqrt{3}$cm và $40\sqrt{3}$ cm;

C. 20 cm và 40 cm;

D. 20 cm và $20\sqrt{3}$cm.

Hướng dẫn giải

Đáp án đúng là: A

Tam giác ABC vuông tại A nên ta có:

⦁AB = AC.tanC = 20.tan60° = $20\sqrt{3}$cm;

⦁AC = BC.cosC, suy ra $BC=\frac{AC}{\cos C}=\frac{20}{\cos 60°}=40$ cm.

Vậy $AB=20\sqrt{3}$ cm, BC = 40 cm. Ta chọn phương án A.

Bài 3. Cho hình thang ABCD vuông tại A và D, $\hat{C}=50°$. Biết AB = 2, $AD=\frac{6}{5}$. Diện tích (làm tròn kết quả đến hàng phần mười) của hình thang ABCD là

A. S_ABCD ≈ 2 (đvdt);

B. S_ABCD ≈ 3 (đvdt);

C. S_ABCD ≈ 4 (đvdt);

D. S_ABCD ≈ $\frac{5}{2}$(đvdt).

Hướng dẫn giải

Đáp án đúng là: B

Kẻ BE ⊥ CD tại E.

Ta có $\widehat{BAD}=\widehat{ADE}=\widehat{BED}=90°$ nên tứ giác ABED là hình chữ nhật.

Do đó $BE=AD=\frac{6}{5}$ và DE = AB = 2.

Tam giác BEC vuông tại E nên $\tan \widehat{BCE}=\frac{BE}{EC}$.

Suy ra $EC=\frac{BE}{\tan \widehat{BCE}}=\frac{\frac{6}{5}}{\tan 50°}\approx 1$.

Do đó DC = DE + EC ≈ 2 + 1 = 3.

Diện tích hình thang vuông ABCD là:

$S_{ABCD}=\frac{1}{2}\cdot AD\cdot \left(AB+CD\right)\approx \frac{1}{2}\cdot \frac{6}{5}\cdot \left(2+3\right)=3$ (đvdt).

Bài 4. Cho tam giác ABC cân tại A, $\hat{B}=65°,$ đường cao CH = $\frac{18}{5}$. Giải tam giác ABC (làm tròn đến hàng phần mười củađơn vị độ dài).

Hướng dẫn giải

Vì tam giác ABC cân tại A nên $\widehat{ACB}=\widehat{ABC}=65°$.

Tam giác ABC, có: $\widehat{BAC}+\widehat{ACB}+\widehat{ABC}=180°$(tổng ba góc của một tam giác)

Suy ra $\widehat{BAC}=180°-\left(\widehat{ACB}+\widehat{ABC}\right)=180°-\left(65°+65°\right)=50°$.

Tam giác BCH vuông tại H nên $\sin \widehat{CBH}=\frac{CH}{BC}$.

Suy ra $BC=\frac{CH}{\sin \widehat{CBH}}=\frac{\frac{18}{5}}{\sin 65°}\approx 4,0$.

Tam giác AHC vuông tại H nên $\sin \widehat{HAC}=\frac{CH}{AC}$.

Suy ra $AC=\frac{CH}{\sin \widehat{HAC}}=\frac{\frac{18}{5}}{\sin 50°}\approx 4,7.$

Vì tam giác ABC cân tại A nên AB = AC ≈ 4,7.

Vậy AB = AC ≈ 4,7; BC ≈ 4; $\widehat{ACB}=65°$ và $\widehat{BAC}=50°$.

Bài 5. Cho tam giác ABC vuông tại A có đường cao AH (H ∈ BC).

a) Cho BC = 12; CH = 9. Tính số đo $\widehat{ABC}$.

b) Lấy điểm D nằm giữa hai điểm A và C. Kẻ AK ⊥ BD. Chứng minh rằng BK.BD = BH.BC.

Hướng dẫn giải

a) Ta có BH = BC – CH = 12 – 9 = 3.

Xét ∆ABH và ∆CBA, có:

$\widehat{AHB}=\widehat{BAC}=90°$;

$\widehat{ABC}$ chung.

Do đó ∆ABH ᔕ ∆CBA (g.g).

Suy ra $\frac{AB}{CB}=\frac{BH}{BA}$.

Khi đó AB² = BC.BH = 12.3 = 36.

Vì vậy AB = 6.

Tam giác ABC vuông tại A nên $\cos \widehat{ABC}=\frac{AB}{BC}=\frac{6}{12}=\frac{1}{2}$.

Suy ra $\widehat{ABC}=60°$.

b) Xét ∆ABK và ∆DBA, có:

$\widehat{AKB}=\widehat{BAD}=90°$;

$\widehat{ABD}$ chung.

Do đó ∆ABK ᔕ ∆DBA (g.g)

Suy ra $\frac{AB}{DB}=\frac{BK}{BA}$ nên AB² = BD.BK.

Mà AB² = BC.BH (câu a)

Vậy BK.BD = BH.BC.

Bài 6. Một cần cẩu đang nâng một khối gỗ trên sông. Biết tay cẩu có chiều dài là 16 m và nghiêng một góc 35° so với phương nằm ngang (như hình vẽ).Tính chiều dài của đoạn dây cáp (làm tròn kết quả đến hàng phần mười).

Hướng dẫn giải

Dựa vào hình vẽ, ta thấy:

⦁ Tay cẩu là đoạn AB có độ dài là 16 m;

⦁ Tay cẩu nghiêng một góc 35° so với phương nằm ngang, tức là $\widehat{BAC}=35°.$

⦁ Chiều dài đoạn dây cáp là đoạn BC.

Tam giác ABC vuông tại C nên:

$BC=AB\cdot \sin \widehat{BAC}=16\cdot \sin 35°\approx 9,2$ (m).

Vậy chiều dài của đoạn dây cáp bằng khoảng 9,2 m.

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Tỉ số lượng giác của góc nhọn

Lý thuyết Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Lý thuyết Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn

Lý thuyết Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn

Lý thuyết Bài 2: Vị trí tương đối của đường thẳng và đường tròn

Lý thuyết Bài 3: Tiếp tuyến của đường tròn