Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số chi tiết sách Toán 9 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

Khởi động trang 61 Toán 9 Tập 1: Để lái xe an toàn khi đi qua đoạn đường có dạng cung tròn, người lái cần biết tốc độ tối đa cho phép là bao nhiêu. Vì thế, ở những đoạn đường đó thường có bảng chỉ dẫn cho tốc độ tối đa cho phép của ô tô. Tốc độ tối đa cho phép $v\left(m/s\right)$ được tính bởi công thức $v=\sqrt{rg\mu }$, trong đó $r\left(m\right)$ là bán kính của cung đường, $g=9,8m/s^2$, $\mu$ là hệ số ma sát trượt của đường.

Hãy viết biểu thức tính $r$ khi biết $\mu =0,12$. Trong toán học, biểu thức đó được gọi là gì?

Lời giải:

$v=\sqrt{r.0,12.9,8}$ nên $v_{}^2=r.1,176$. Vậy $r=\frac{v_{}^2}{1,176}$.

Đây là biểu thức bậc hai.

Hoạt động 1 trang 61 Toán 9 Tập 1: Cửa hàng điện máy trưng bày một chiếc ti vi màn hình phẳng 55in, tức là độ dài đường chéo của màn hình tivi bằng 55in (1in = 2,54cm). Gọi $x\left(in\right)$ là chiều rộng của màn hìn tivi (Hình 5). Viết công thức tính chiều dài của màn hình ti vi theo $x$.

Lời giải:

Chiều dài của màn hình ti vi là: $\sqrt{{55}^2-x^2}$.

1. Căn thức bậc hai

Luyện tập 1 trang 62 Toán 9 Tập 1: Mỗi biểu thức sau có phải là một căn thức bậc hai hay không?

a. $\sqrt{2x-5}$.

b. $\sqrt{\frac{1}{x}}$.

c. $\frac{1}{x+1}$.

Lời giải:

a. Biểu thức $\sqrt{2x-5}$ là một căn thức bậc hai vì $2x-5$ là một biểu thức đại số.

b. Biểu thức $\sqrt{\frac{1}{x}}$ là một căn thức bậc hai vì $\frac{1}{x}$ là một biểu thức đại số.

c. Biểu thức $\frac{1}{x+1}$ không là một căn thức bậc hai.

Luyện tập 2 trang 62 Toán 9 Tập 1: Tính giá trị của $\sqrt{2x^2+1}$ tại:

a. $x=2$;

b. $x=-\sqrt{12}$.

Lời giải:

a. Thay $x=2$ vào biểu thức, ta được: $\sqrt{{2.2}^2+1}=\sqrt{9}=3$.

b. Thay $x=-\sqrt{12}$ vào biểu thức, ta được: $\sqrt{2.{\left(-\sqrt{12}\right)}^2+1}=\sqrt{25}=5$.

Hoạt động 2 trang 62 Toán 9 Tập 1: Cho căn thức bậc hai $\sqrt{x-1}$. Biểu thức đó có xác định hay không tại mỗi giá trị sau?

a. $x=0$.

b. $x=1$.

c. $x=2$.

Lời giải:

a. Thay $x=0$ vào biểu thức, ta được: $\sqrt{0-1}=\sqrt{-1}$.

Vậy biểu thức đã cho không xác định.

b. Thay $x=1$ vào biểu thức, ta được: $\sqrt{1-1}=\sqrt{0}=0$.

Vậy biểu thức đã cho xác định.

c. Thay $x=2$ vào biểu thức, ta được: $\sqrt{2-1}=\sqrt{1}=1$.

Vậy biểu thức đã cho xác định.

Luyện tập 3 trang 63Toán 9 Tập 1: Tìm điều kiện xác định cho mỗi căn thức bậc hai sau:

a. $\sqrt{x+1}$;

b. $\sqrt{x^2+1}$.

Lời giải:

a. $\sqrt{x+1}$ xác định khi $x+1\ge 0$ hay $x\ge -1$.

b. $\sqrt{x^2+1}$ xác định khi $x^2+1\ge 0$ (đúng $\mathrm{\forall }x\in \mathbb{R}$).

2. Căn thức bậc ba

Hoạt động 3 trang 63 Toán 9 Tập 1: Thể tích V của một khối lập phương được tính bởi công thức: $V=a^3$ với a là độ dài cạnh của khối lập phương. Viết công thức tính độ dài cạnh của khối lập phương theo thể tích V của nó.

Lời giải:

Công thức tính độ dài cạnh của khối lập phương là: $a=\sqrt[3]{V}$.

Luyện tập 4 trang 64 Toán 9 Tập 1: Mỗi biểu thức sau có phải là một căn thức bậc ba hay không?

a. $\sqrt[3]{2x^2-7}$;

b. $\sqrt[3]{\frac{1}{5x-4}}$;

c. $\frac{1}{7x+1}$.

Lời giải:

a. Biểu thức $\sqrt[3]{2x^2-7}$ là một căn thức bậc ba vì $2x^2-7$ là một biểu thức đại số.

b. Biểu thức $\sqrt[3]{\frac{1}{5x-4}}$ là một căn thức bậc ba vì $\frac{1}{5x-4}$ là một biểu thức đại số.

c. Biểu thức $\frac{1}{7x+1}$ không là một căn thức bậc ba.

Luyện tập 5 trang 64 Toán 9 Tập 1: Tính giá trị của $\sqrt[3]{x^3}$ tại $x=3;x=-2;x=-10$.

Lời giải:

Thay $x=3$ vào biểu thức, ta được: $\sqrt[3]{3^3}=\sqrt[3]{27}=3$.

Thay $x=-2$ vào biểu thức, ta được: $\sqrt[3]{{\left(-2\right)}^3}=\sqrt[3]{-8}=-2$.

Thay $x=-10$ vào biểu thức, ta được: $\sqrt[3]{{\left(-10\right)}^3}=\sqrt[3]{-1000}=-10$.

Hoạt động 4 trang 64 Toán 9 Tập 1: Cho căn thức bậc ba $\sqrt[3]{\frac{2}{x-1}}$. Biểu thức đó có xác định hay không tại mỗi giá trị sau?

a. $x=17$.

b. $x=1$.

Lời giải:

a. Thay $x=17$ vào biểu thức, ta được: $\sqrt[3]{\frac{2}{17-1}}=\sqrt[3]{\frac{2}{16}}=\sqrt[3]{\frac{1}{8}}=\frac{1}{2}$.

Vậy biểu thức đã cho xác định.

b. Thay $x=1$ vào biểu thức, ta được: $\sqrt[3]{\frac{2}{1-1}}=\sqrt[3]{\frac{2}{0}}$.

Do $\frac{2}{0}$ không xác định nên biểu thức đã cho không xác định.

Luyện tập 6 trang 64 Toán 9 Tập 1: Tìm điều kiện xác dịnh cho mỗi căn thức bậc ba sau:

a. $\sqrt[3]{x^2+x}$

b. $\sqrt[3]{\frac{1}{x-9}}$

Lời giải:

a. $\sqrt[3]{x^2+x}$ xác định với mọi số thực $x$ vì $x^2+x$ xác định với mọi số thực $x$.

b. $\sqrt[3]{\frac{1}{x-9}}$ xác định với $x\ne 9$ vì $\frac{1}{x-9}$ xác định với $x\ne 9$.

Bài tập

Bài 1 trang 65 Toán 9 Tập 1: Tính giá trị của mỗi căn thức bậc hai sau:

a. $\sqrt[]{17-x^2}$ tại $x=1;x=-3;x=2\sqrt[]{2}$;

b. $\sqrt[]{x^2+x+1}$ tại $x=0;x=-1;x=-7$.

Lời giải:

a. Thay $x=1$ vào biểu thức, ta được: $\sqrt{17-1^2}=\sqrt{17-1}=\sqrt{16}=4$.

Thay $x=-3$ vào biểu thức, ta được: $\sqrt{17-{\left(-3\right)}^2}=\sqrt{17-9}=\sqrt{8}$.

Thay $x=2\sqrt{2}$ vào biểu thức, ta được: $\sqrt{17-{\left(2\sqrt{2}\right)}^2}=\sqrt{17-8}=\sqrt{9}=3$.

b. Thay $x=0$ vào biểu thức, ta được: $\sqrt{0^2+0+1}=\sqrt{1}=1$.

Thay $x=-1$ vào biểu thức, ta được: $\sqrt{{\left(-1\right)}^2+\left(-1\right)+1}=\sqrt{1}=1$.

Thay $x=-7$ vào biểu thức, ta được: $\sqrt{{\left(-7\right)}^2+\left(-7\right)+1}=\sqrt{49-7+1}=\sqrt{43}$.

Bài 2 trang 65 Toán 9 Tập 1: Tìm điều kiện xác định cho mỗi căn thức bậc hai sau:

a. $\sqrt[]{x-6}$

b. $\sqrt[]{17-x}$

c. $\sqrt[]{\frac{1}{x}}$

Lời giải:

a. $\sqrt{x-6}$ xác định khi $x-6\ge 0$ hay $x\ge 6$.

b. $\sqrt{17-x}$ xác định khi $17-x\ge 0$ hay $x\le 17$.

c. $\sqrt{\frac{1}{x}}$ xác định khi $\frac{1}{x}\ge 0$ và $x\ne 0$ hay $x>0$.

Bài 3 trang 65 Toán 9 Tập 1: Tính giá trị của mỗi căn thức bậc ba sau:

a. $\sqrt[3]{2x-7}$ tại $x=-10;x=7,5;x=-0,5$

b. $\sqrt[3]{x^2+4}$ tại $x=0;x=2;x=\sqrt[]{23}$.

Lời giải:

a. Thay $x=-10$ vào biểu thức, ta được: $\sqrt[3]{2.\left(-10\right)-7}=\sqrt[3]{-20-7}=\sqrt[3]{-27}=-3$.

Thay $x=7,5$ vào biểu thức, ta được: $\sqrt[3]{2.7,5-7}=\sqrt[3]{15-7}=\sqrt[3]{8}=2$.

Thay $x=-0,5$ vào biểu thức, ta được: $\sqrt[3]{2.\left(-0,5\right)-7}=\sqrt[3]{-1-7}=\sqrt[3]{-8}=-2$.

b. Thay $x=0$ vào biểu thức, ta được: $\sqrt[3]{0^2+4}=\sqrt[3]{4}$.

Thay $x=2$ vào biểu thức, ta được: $\sqrt[3]{2^2+4}=\sqrt[3]{4+4}=\sqrt[3]{8}=2$.

Thay $x=\sqrt[]{23}$ vào biểu thức, ta được: $\sqrt[3]{{\left(\sqrt[]{23}\right)}^2+4}=\sqrt[3]{23+4}=\sqrt[3]{27}=3$.

Bài 4 trang 66 Toán 9 Tập 1: Tìm điều kiện xác định cho mỗi căn thức bậc ba sau:

a. $\sqrt[3]{3x+2}$

b. $\sqrt[3]{x^3-1}$

c. $\sqrt[3]{\frac{1}{2-x}}$

Lời giải:

a. $\sqrt[3]{3x+2}$ xác định với mọi số thực $x$ vì $3x+2$ xác định với mọi số thực $x$.

b. $\sqrt[3]{x^3-1}$ xác định với mọi số thực $x$ vì $x^3-1$ xác định với mọi số thực $x$.

c. $\sqrt[3]{\frac{1}{2-x}}$ xác định với $x\ne 2$ vì $\frac{1}{2-x}$ xác định với $x\ne 2$.

Bài 5 trang 66 Toán 9 Tập 1: Có hai xã A, B cùng ở một bên bờ sông Lam, khoảng cách từ hai xác đó đến bờ sông lần lượt là $A{A}^{\prime }=500m,B{B}^{\prime }=600m$ và người ta đo dược $A^{\prime }{B}^{\prime }=2200m$. Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Giả sử vị trí của trạm cung cấp nước sạch đó là điểm M trên đoạn $A^{\prime }{B}^{\prime }$ với $M{A}^{\prime }=x\left(m\right)$, $0<x<2200$ (minh họa ở Hình 6).

a. Hãy tính tổng khoảng cách $MA+MB$ theo $x$.

b. Tính tổng khoảng cách $MA+MB$ khi $x=1200$ (làm tròn kết quả đến hàng đơn vị của mét).

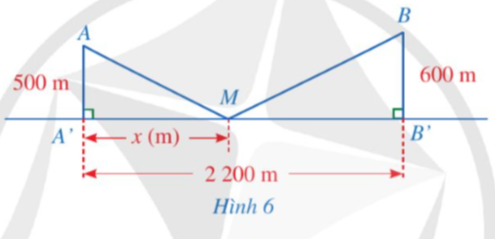
Lời giải:

a. Ta có: $MB=2200-x$

Áp dụng định lý Py – ta – go vào tam giác MAA’ ta có:

$\begin{array}{l}M{A}^2=MA{}^{\prime 2}+AA{}^{\prime 2}\\ M{A}^2=x^2+{500}^2\\ MA=\sqrt{x^2+{500}^2}\end{array}$

Áp dụng định lý Py – ta – go vào tam giác $MB{B}^{\prime }$ ta có:

$\begin{array}{l}M{B}^2=BB{}^{\prime 2}+MB{}^{\prime 2}\Rightarrow M{B}^2={600}^2+{\left(2200-x\right)}^2\\ M{B}^2=360000+4840000-4400x+x^2=5200000-4400x+x^2\\ MB=\sqrt{5200000-4400x+x^2}\end{array}$

Vậy $MA+MB=\sqrt{x^2+{500}^2}+\sqrt{5200000-4400x+x^2}$.

b. Thay $x=1200$vào biểu thức tính $MA+MB$, ta được:

$\begin{array}{l}MA+MB=\sqrt{{1200}^2+{500}^2}+\sqrt{5200000-4400.1200+{1200}^2}\\ =\sqrt{1440000+250000}+\sqrt{5200000-5280000+1440000}\\ =\sqrt{1690000}+\sqrt{1360000}\\ MA+MB\approx 2466\left(cm\right)\approx 24\left(m\right).\end{array}$

Bài 6 trang 66 Toán 9 Tập 1: Hệ quả của hiện tượng nóng lên toàn cầu là băng của một số sông băng đang tan chảy. Mười hai năm sau khi băng biến mất, những loài thực vật nhỏ bé, được gọi là địa y, bắt đầu mọc trên đá. Mỗi nhóm địa y phát triển ở dạng (gần như) một hình tròn. Đường kính $d\left(mm\right)$ của hình tròn này và tuổi của địa y có thể được tính gần đúng bằng công thức: $d=7\sqrt{t-12}$ với t là số năm tính từ khi băng biến mất $\left(t\ge 12\right)$. Tính đường kính của hình tròn do địa y tạo nên sau khi băng biến mất 13 năm; 16 năm.

Lời giải:

Đường kính của hình tròn do địa y tạo nên sau khi băng biến mất 13 năm là:

$d=7\sqrt{13-12}=7\sqrt{1}=7\left(mm\right)$.

Đường kính của hình tròn do địa y tạo nên sau khi băng biến mất 16 năm là:

$d=7.\sqrt{16-12}=7\sqrt{4}=14\left(mm\right)$.

Bài 7 trang 66 Toán 9 Tập 1: Chiều cao ngang vai của một con voi đực ở châu Phi là h (cm) có thể được tính xấp xỉ bằng công thức: $h=62,5.\sqrt[3]{t}+75,8$ với t là tuổi của con voi tính theo năm.

a. Một con voi đực 8 tuổi có chiều cao ngang vai là bao nhiêu centimét?

b. Nếu một con voi đực có chiều cao ngang vai là 205cm thì con voi đó bao nhiêu tuổi (làm tròn kết quả đến hàng đơn vị)?

Lời giải:

a. Một con voi đực 8 tuổi thì có chiều cao ngang vai là: $h=62,5.\sqrt[3]{8}+75,8=62,5.2+75,8=200,8\left(cm\right)$

b. Nếu một con voi đực có chiều cao ngang vai là 205cm thì con voi đó số tuổi là:

$\begin{array}{l}205=62,5\sqrt[3]{t}+75,8\\ \sqrt[3]{t}=2,0672\\ t\approx 9\end{array}$

Vậy nếu một con voi đực có chiều cao ngang vai là 205cm thì con voi đó 9 tuổi.

Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

§2. Một số phép tính về căn bậc hai của số thực

§3. Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

§4. Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Bài tập cuối chương 3

§1. Tỉ số lượng giác của góc nhọn

§2. Một số hệ thức về cạnh và góc trong tam giác vuông

Lý thuyết Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

1. Căn thức bậc hai

Khái niệm căn thức bậc hai

Ví dụ: $\sqrt{2x-1}$, $\sqrt{-\frac{1}{3}{x}^2+2}$ là các căn thức bậc hai.

Điều kiện xác định của căn thức bậc hai

Ví dụ: Điều kiện xác định của căn thức $\sqrt{2x+1}$ là $2x+1\ge 0$ hay $x\ge -\frac{1}{2}$.

Điều kiện xác định của căn thức $\sqrt{-\frac{1}{3}x+2}$ là $-\frac{1}{3}x+2\ge 0$ hay $x\le 6$.

2. Căn thức bậc ba

Khái niệm căn thức bậc ba

Chú ý: Các số, biến số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, khai căn (bậc hai hay bậc ba) làm thành một biểu thức đại số.

Ví dụ: $\sqrt[3]{x}$, $\sqrt[3]{\frac{1}{x+1}}$ là các căn thức bậc ba.

Điều kiện xác định của căn thức bậc ba

Ví dụ:

$\sqrt[3]{5x-11}$ xác định với mọi số thực x vì $5x-11$ xác định với mọi số thực x.

$\sqrt[3]{\frac{1}{x-1}}$ xác định với $x\ne 1$ vì $\frac{1}{x-1}$ xác định với $x\ne 1$.