Với tóm tắt lý thuyết Toán lớp 9 Bài 4: Hình quạt tròn và hình vành khuyên sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.
Lý thuyết Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên
A. Lý thuyết Hình quạt tròn và hình vành khuyên
1. Độ dài cung tròn
Công thức tính chu vi đường tròn
Công thức tính độ dài C của đường tròn (O; R), đường kính d = 2R là:
Công thức tính độ dài cung tròn
|
Trên đường tròn bán kính R, độ dài l của một cung có số đo được tính theo công thức: . |
Ví dụ:
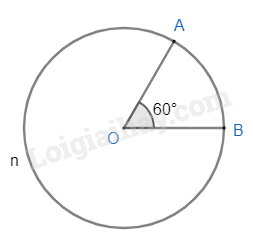
Đường tròn (O; 2cm), .
- Cung nhỏ AB bị chắn bởi góc ở tâm AOB.
Do đó sđ
Độ dài của cung AB là:
Cung lớn AnB có số đo là:
sđ.
Độ dài của cung AnB là:
2. Hình quạt tròn
Khái niệm hình quạt tròn
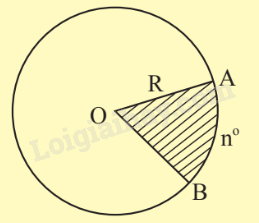
|
Hình quạt tròn là một phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai mút của cung đó. |
Diện tích hình quạt tròn
|
Diện tích hình quạt tròn bán kính R ứng với cung :
|
Ví dụ: Diện tích hình quạt tròn có độ dài tương ứng với nó là cm, bán kính là R = 5cm là:
3. Hình vành khuyên
Khái niệm hình vành khuyên
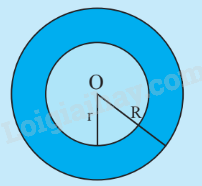
|
Cho hai đường tròn đồng tâm và với . Hình vành khuyên là phần mặt phẳng giới hạn bởi hai đường tròn (O;r) và (O;R) được tính bởi công thức: . |
Diện tích hình vành khuyên
|
Diện tích của hình vành khuyên tạo bởi hai đường tròn đồng tâm và có bán kính R và r: (với R > r) |
Ví dụ: Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là:
Sơ đồ tư duy Hình quạt tròn và hình vành khuyên
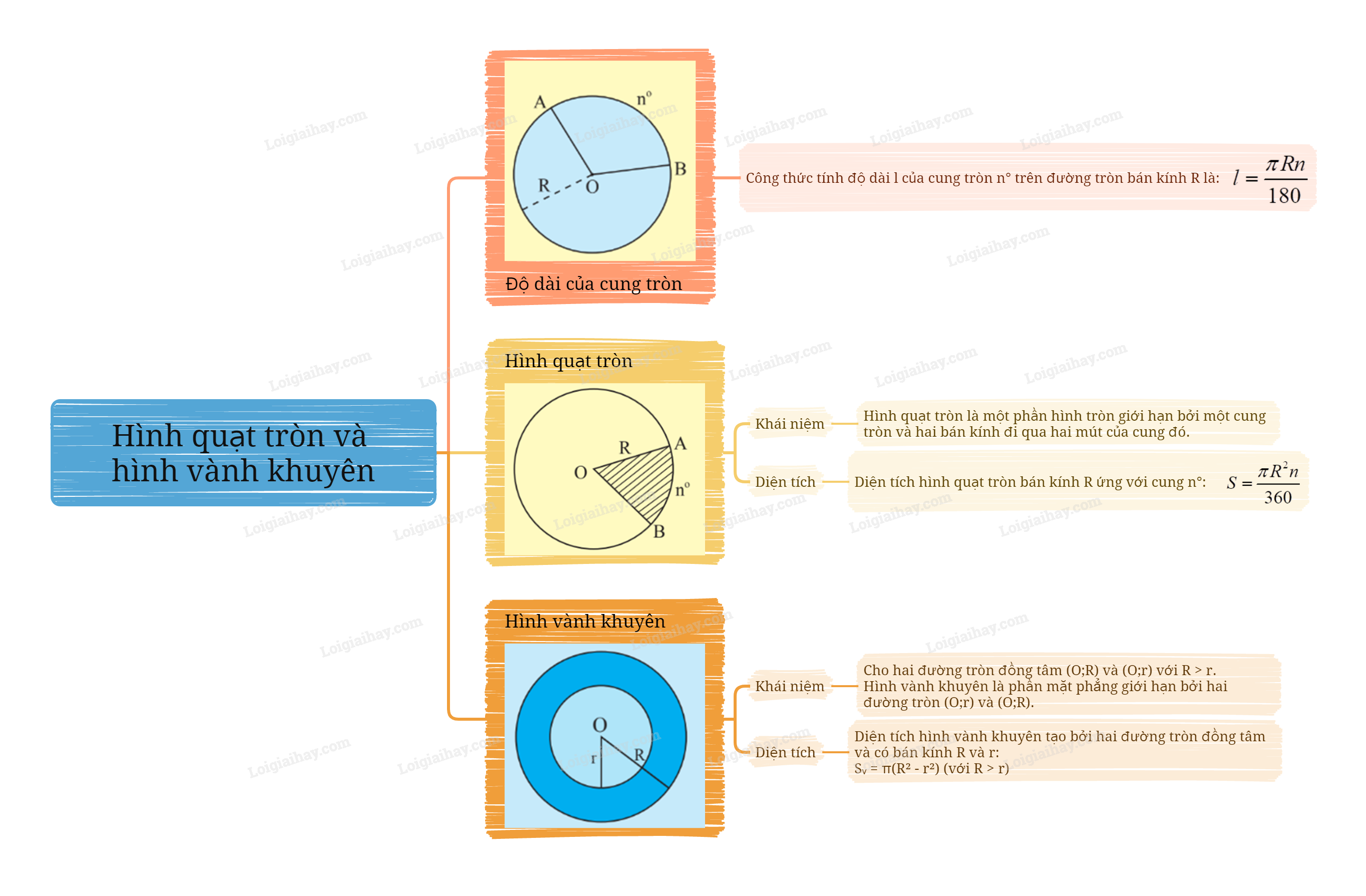
B. Bài tập Hình quạt tròn và hình vành khuyên
Bài 1. Diện tích hình quạt tròn bán kính R, ứng với cung 45° là
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: D
Diện tích hình quạt tròn bán kính R, ứng với cung 45° là:
Diện tích hình quạt tròn bán kính R, ứng với cung 45° là
Bài 2. Diện tích hình vành khuyên giới hạn bởi đường tròn (O; 1 cm) và (O; 3 cm) là
A. 10 cm2;
B. 8 cm2;
C. 8π cm2;
D. 10π cm2.
Hướng dẫn giải
Đáp án đúng là: C
Diện tích hình vành khuyên giới hạn bởi đường tròn (O; 1 cm) và (O; 3 cm) là:
(cm2).
Bài 3. Cho đường tròn (O; 5 cm).
a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây bằng 2,5 cm;
b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm);
c) Tính số đo và độ dài của cung nhỏ AB;
d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.
Hướng dẫn giải
Theo đề bài, ta có hình vẽ sau:
a) Vẽ bán kính OM của đường tròn, trên OM lấy điểm H sao cho OH = 2,5 cm.
Kẻ đoạn thẳng AB vuông góc với OH tại H, cắt đường tròn tại A và B.
Khi đó, ta được dây cung AB cần vẽ.
b) Gọi H là trung điểm của AB.
Xét ∆OAH và ∆OBH có:
OA = OB = R; OH chung; .
Do đó ∆OAH = ∆OBH (cạnh huyền – cạnh góc vuông)
Suy ra AH = BH (hai cạnh tương ứng) và AB = 2AH.
Xét ∆OAH vuông tại H có: AH2 + OH2 = OA2 (định lí Pythagore)
Hay AH2 = OA2 – OH2 = 52 – 2,52 = 18,75.
Suy ra (cm) và (cm).
Vậy độ dài của dây AB khoảng 8,66 cm.
c) Xét ∆OAH vuông tại H có:
suy ra
Mà ∆OAH = ∆OBH suy ra (hai góc tương ứng)
Suy ra và
Độ dài cung AB là: (cm).
Vậy và độ dài cung nhỏ AB bằng .
d) Diện tích hình quạt tròn ứng với cung nhỏ AB là:
(cm2).
Vậy diện tích hình quạt tròn ứng với cung nhỏ AB bằng cm2.
Bài 4. Tính độ dài các cung 60°; 90°; 150° của đường tròn (O; 5 cm) (làm tròn kết quả đến hàng phần trăm).
Hướng dẫn giải
Cung 60°, bán kính R = 5 cm có độ dài là: (cm).
Cung 90°, bán kính R = 5 cm có độ dài là: (cm).
Cung 150°, bán kính R = 5 cm có độ dài là:
Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 1: Tỉ số lượng giác của góc nhọn
Lý thuyết Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông
Lý thuyết Bài 2: Tiếp tuyến của đường tròn
Lý thuyết Bài 3: Góc ở tâm, góc nội tiếp
Lý thuyết Bài 4: Hình quạt tròn và hình vành khuyên