Với tóm tắt lý thuyết Toán lớp 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông

A. Lý thuyết Hệ thức giữa cạnh và góc của tam giác vuông

1. Hệ thức giữa cạnh và góc của tam giác vuông

Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn

Ví dụ 1:

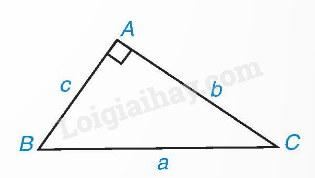
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=a.\sin B=a.\cos C;\\ c=a.\sin C=a.\cos B.\end{array}$

Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn

Ví dụ 2:

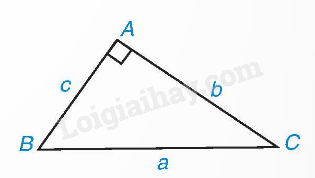
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=c.\tan B=c.\cot C;\\ c=b.\tan C=b.\cot B.\end{array}$

2. Giải tam giác vuông

Giải tam giác vuông là tính các cạnh và góc chưa biết của tam giác đó.

Sơ đồ tư duy Hệ thức giữa cạnh và góc của tam giác vuông

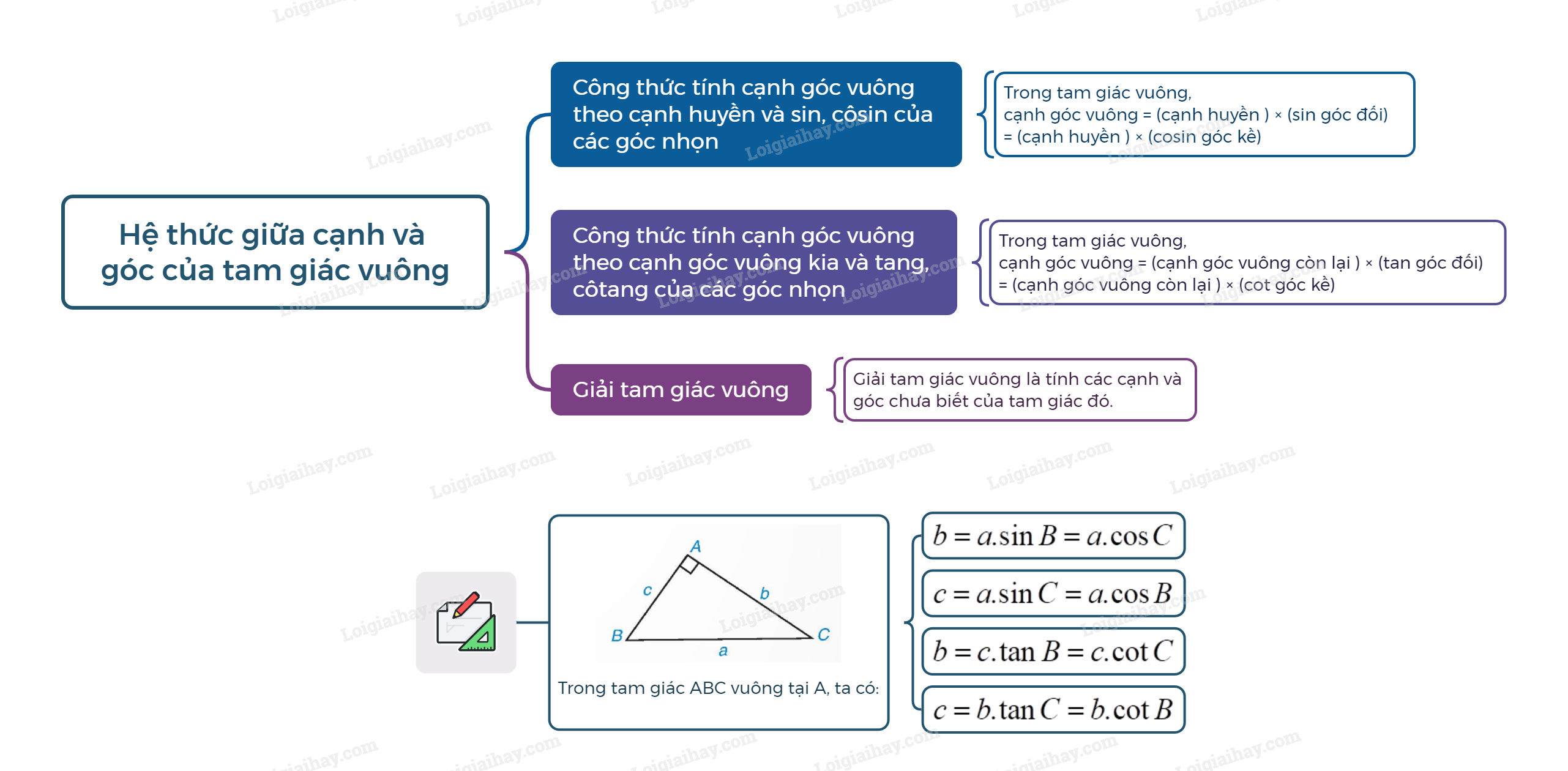
B. Bài tập Hệ thức giữa cạnh và góc của tam giác vuông

Bài 1. Cho tam giác ABC vuông tại A có AB = 5 cm, $\widehat{B}=30°.$ Độ dài hai cạnh còn lại là:

A. $AC=\frac{5\sqrt{3}}{3}$ cm; $BC=\frac{10\sqrt{3}}{3}$ cm;

B. $AC=\frac{10\sqrt{3}}{3}$ cm; $BC=\frac{5\sqrt{3}}{3}$ cm;

C. $AC=5\sqrt{3}$ cm; $BC=10\sqrt{3}$ cm;

D. $AC=\frac{10}{3}$ cm; $BC=\frac{5}{3}$ cm.

Hướng dẫn giải

Đáp án đúng là: A

Ta có: $\tan B=\frac{AC}{AB}$ nên $AC=AB.\tan B=5.\tan 30°=\frac{5\sqrt{3}}{3}$ cm.

Áp dụng định lí Pythagore, ta có:

$B{C}^2=A{B}^2+A{C}^2=5^2+{\left(\frac{5\sqrt{3}}{3}\right)}^2=\frac{100}{3}$.

Suy ra $BC=\sqrt{\frac{100}{3}}=\frac{10\sqrt{3}}{3}$ cm.

Bài 2. Cho tam giác DEF có $\widehat{E}=60°,$$\widehat{F}=42°,$ đường cao DS = 12 cm (như hình vẽ)

Độ dài của cạnh EF của tam giác DEF (kết quả làm tròn đến hàng phần mười) bằng

A. 25,6 cm;

B. 19,8 cm;

C. 20,2 cm;

D. 18,6 cm.

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác DEF có DS là đường cao, ta có: $\widehat{DSE}=\widehat{DSF}=90°.$

Suy ra tam giác DES vuông tại S và tam giác DFS vuông tại S.

Xét tam giác DES vuông tại S, ta có:

$\tan E=\frac{DS}{ES}$ nên $ES=\frac{DS}{\tan E}=\frac{12}{\tan 60°}=\frac{12}{\sqrt{3}}=4\sqrt{3}\approx 6,9$ cm.

Xét tam giác DES vuông tại S, ta có:

$\tan F=\frac{DS}{FS}$ nên $FS=\frac{DS}{\tan F}=\frac{12}{\tan 42°}\approx 13,3$ cm.

Mà EF = ES + FS = 6,9 + 13,3 = 20,2 cm.

Vậy độ dài cạnh EF là 20,2 cm.

Bài 3. Cho tam giác ABC vuông tại A có đường cao AH và góc B = α. Tìm giá trị α sao cho BH = 3CH.

Hướng dẫn giải

Theo đề bài, ta có hình vẽ sau:

Đặt AH = h.

Xét tam giác ABH vuông tại H, ta có:

BH = AH.cot B = h.cot α.

Xét tam giác ACH vuông tại H, ta có:

CH = AH.cot C = AH.tan B = h.tan α.

BH = 3CH suy ra $\frac{BH}{CH}=\frac{h.\cot \alpha }{h.\tan \alpha }=\frac{\frac{1}{\tan \alpha }}{\tan \alpha }=\frac{1}{{\tan }^2\alpha }=3$

Do đó $\tan \alpha =\frac{\sqrt{3}}{3}=\tan 30°.$

Vậy α = 30°.

Bài 4. Một cầu trượt ở công viên có độ dốc là 28° và độ cao là 1,8 m. Tìm độ dài của mặt cầu trượt.

Hướng dẫn giải

Áp dụng hệ thức về cạnh và góc trong tam giác vuông ABC vuông tại A.

Khi đó, độ dài mặt cầu trượt là:

$AB=\frac{1,8}{\sin 28°}\approx 3,83$ (m).

Vậy độ dài của mặt cầu trượt khoảng 3,83 m.

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 1: Tỉ số lượng giác của góc nhọn

Lý thuyết Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông

Lý thuyết Bài 1: Đường tròn

Lý thuyết Bài 2: Tiếp tuyến của đường tròn

Lý thuyết Bài 3: Góc ở tâm, góc nội tiếp

Lý thuyết Bài 4: Hình quạt tròn và hình vành khuyên