Với tóm tắt lý thuyết Toán lớp 9 Bài 1: Tỉ số lượng giác của góc nhọn sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn

A. Lý thuyết Tỉ số lượng giác của góc nhọn

1. Định nghĩa tỉ số lượng giác của một góc nhọn

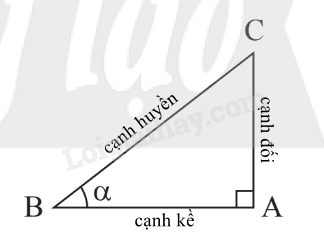
Tip học thuộc nhanh:

Chú ý: Với góc nhọn $\alpha$, ta có:

$0<\sin \alpha <1$; $0<\cos \alpha <1$.

$\cot \alpha =\frac{1}{\tan \alpha }$.

Ví dụ:

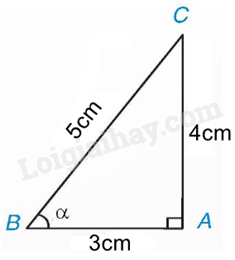
Theo định nghĩa của tỉ số lượng giác, ta có:

$\sin \alpha =\frac{AC}{BC}=\frac{4}{5}$, $\cos \alpha =\frac{AB}{BC}=\frac{3}{5}$, $\tan \alpha =\frac{AC}{AB}=\frac{4}{3}$, $\cot \alpha =\frac{AB}{AC}=\frac{3}{4}$

Bảng giá trị lượng giác của các góc nhọn đặc biệt

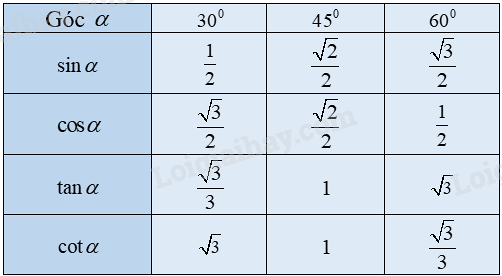
Ví dụ: $P=\frac{\sin {30}^0.\cos {60}^0}{\tan {45}^0}=\frac{\frac{1}{2}.\frac{1}{2}}{1}=\frac{1}{4}$.

2. Tỉ số lượng giác của hai góc phụ nhau

Định lí về tỉ số lượng giác của hai góc phụ nhau

Ví dụ:

$\begin{array}{l}\sin {60}^0=\cos \left({90}^0-{60}^0\right)=\cos {30}^0;\\ \cos {52}^0{30}^{\prime }=\sin \left({90}^0-{52}^0{30}^{\prime }\right)=\sin {37}^0{30}^{\prime };\\ \tan {80}^0=\cot \left({90}^0-{80}^0\right)=\cot {10}^0;\\ \cot {82}^0=\tan \left({90}^0-{82}^0\right)=\tan 8^0.\end{array}$

3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn

Người ta thường dùng các đơn vị số đo góc là độ (kí hiệu: ${}^0$), phút (kí hiệu: ${}^{\prime }$), giây (kí hiệu: ${}^{″}$).

Ta có thể sử dụng nhiều loại máy tính cầm tay để tính các tỉ số lượng giác của góc nhọn và tính số đo của góc nhọn khi biết một tỉ số lượng giác của nó.

Lưu ý: ta cần đổi đơn vị đo về độ.

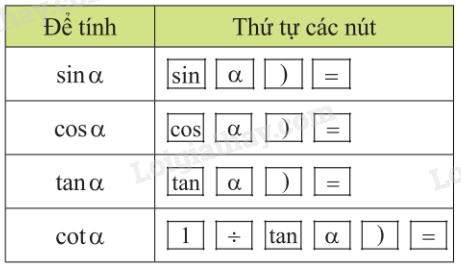
Tính các tỉ số lượng giác của các góc nhọn

Để tính tỉ số lượng giác của một góc $\alpha$, ta dùng các nút:

Để tính $\cot \alpha$, ta tính $\cot \alpha =\frac{1}{\tan \alpha }$ hoặc $\tan \left({90}^0-\alpha \right)$.

Bảng tóm tắt cách tính tỉ số lượng giác của một góc nhọn

Xác định số đo của góc nhọn khi biết một tỉ số lượng giác của góc đó

Bảng tóm tắt cách tính số đo của một góc nhọn khi biết một tỉ số lượng giác

Để tìm $\alpha$ khi biết $\cot \alpha$, ta tính $\tan \alpha =\frac{1}{\cot \alpha }$ và dùng $\tan \alpha$ để tính $\alpha$.

Một số công thức mở rộng:

+) ${\sin }^2\alpha +{\cos }^2\alpha =1$

+) $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$

+) $\cot \alpha =\frac{\cos \alpha }{\sin \alpha }$

+) $\tan \alpha .\cot \alpha =1$

+) $\frac{1}{{\cos }^2\alpha }={\tan }^2\alpha +1$

+) $\frac{1}{{\sin }^2\alpha }={\cot }^2\alpha +1$

Sơ đồ tư duy Tỉ số lượng giác của góc nhọn

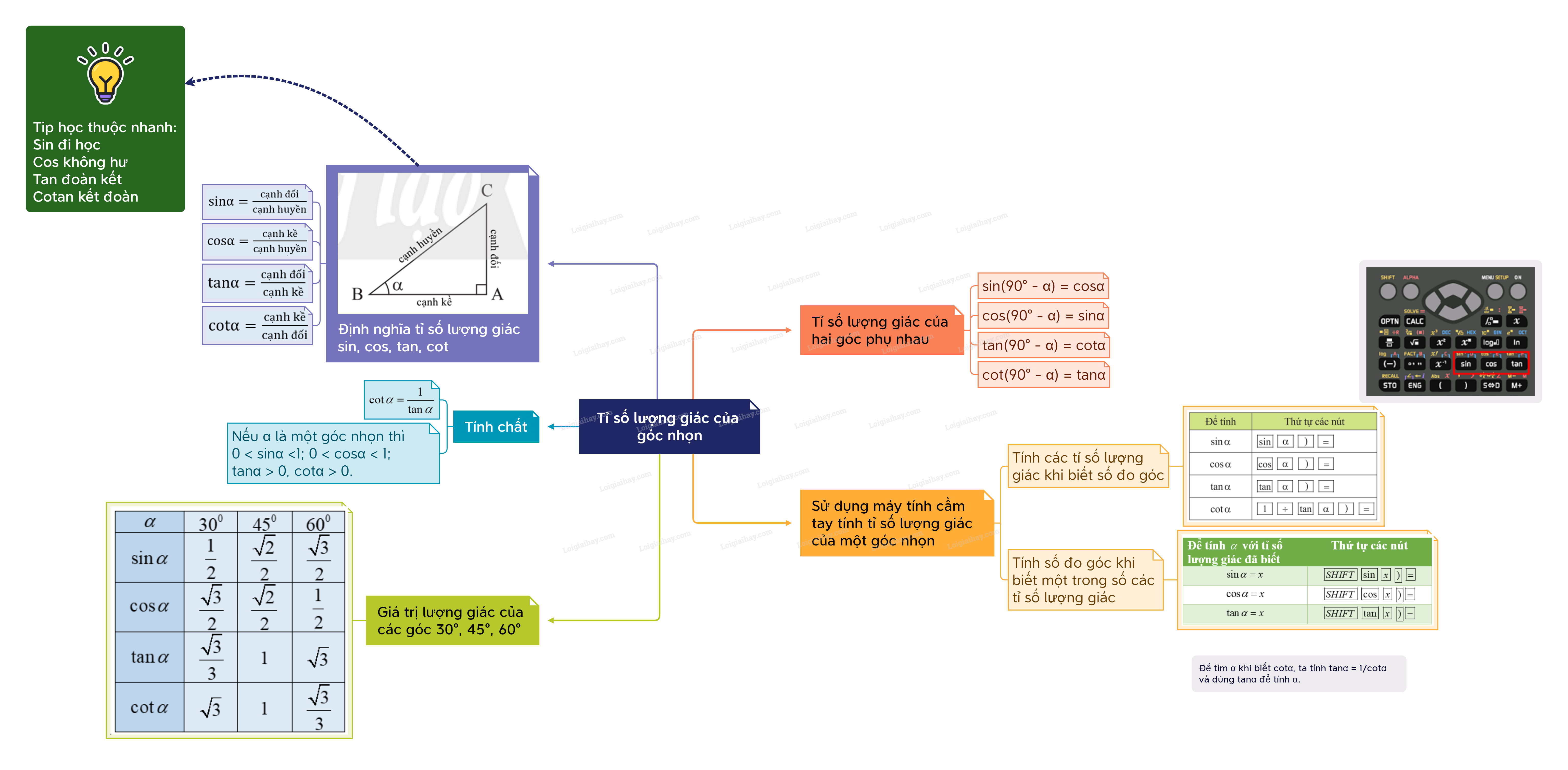
B. Bài tập Tỉ số lượng giác của góc nhọn

Bài 1. Cho α là góc nhọn bất kỳ. Chọn khẳng định đúng.

A. $\sin \alpha +\cos \alpha =1;$

B. ${\sin }^2\alpha +{\cos }^2\alpha =1;$

C. ${\sin }^3\alpha +{\cos }^3\alpha =1;$

D. $\sin \alpha -\cos \alpha =1.$

Hướng dẫn giải

Đáp án đúng là: B

Cho α là góc nhọn bất kỳ, khi đó ${\sin }^2\alpha +{\cos }^2\alpha =1.$

Bài 2. Cho α là góc nhọn bất kỳ. Chọn khẳng định sai.

A. $\tan \alpha =\frac{\sin \alpha }{\cos \alpha };$

B. $\cot \alpha =\frac{\cos \alpha }{\sin \alpha };$

C. $\tan \alpha .\cot \alpha =1;$

D. ${\tan }^2\alpha -1={\cos }^2\alpha .$

Hướng dẫn giải

Đáp án đúng là: D

Cho α là góc nhọn bất kỳ, khi đó:

• ${\sin }^2\alpha +{\cos }^2\alpha =1;$$\tan \alpha .\cot \alpha =1.$

• $\tan \alpha =\frac{\sin \alpha }{\cos \alpha };$$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }.$

• $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha };$$1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }.$

Bài 3. Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác của góc B trong mỗi trường hợp sau:

a) BC = 12 cm; AB = 8 cm;

b) $AB=a\sqrt{2};$$AC=2\sqrt{2}a.$

Hướng dẫn giải

a) Theo định lí Pythagore, ta có: BC² = AB² + AC²

Suy ra AC² = BC² – AB² = 12² – 8² = 80.

Do đó $AC=4\sqrt{5}$ cm.

Các tỉ số lượng giác của góc B là:

• $\sin B=\frac{AC}{BC}=\frac{4\sqrt{5}}{12}=\frac{\sqrt{5}}{3};$$\cos B=\frac{AB}{BC}=\frac{8}{12}=\frac{2}{3}.$

• $\tan B=\frac{AC}{AB}=\frac{4\sqrt{5}}{8}=\frac{\sqrt{5}}{2};$$\cot B=\frac{AB}{AC}=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}.$

Vậy $\sin B=\frac{\sqrt{5}}{3};\cos B=\frac{2}{3};\tan B=\frac{\sqrt{5}}{2};\cot B=\frac{2\sqrt{5}}{5}.$

b) Theo định lí Pythagore, ta có: BC² = AB² + AC²

$={\left(a\sqrt{2}\right)}^2+{\left(2\sqrt{2}a\right)}^2$$=2a^2+8a^2$$=10a^2$

Suy ra $BC=a\sqrt{10}.$

Các tỉ số lượng giác của góc B là:

• $\sin B=\frac{AC}{BC}=\frac{2\sqrt{2}a}{a\sqrt{10}}=\frac{2\sqrt{5}a}{5};$$\cos B=\frac{AB}{BC}=\frac{a\sqrt{2}}{a\sqrt{10}}=\frac{\sqrt{5}}{5}.$

• $\tan B=\frac{AC}{AB}=\frac{2\sqrt{2}a}{a\sqrt{2}}=2;$$\cot B=\frac{1}{\tan B}=\frac{1}{2}.$

Vậy $\sin B=\frac{2\sqrt{5}a}{5};\cos B=\frac{\sqrt{5}}{5};\tan B=2;\cot B=\frac{1}{2}.$

Bài 4. Rút gọn và tính các biểu thức sau:

a) $A=\sin 15°-\sin 60°+\cos 30°-\cos 75°+5;$

b) $B={\sin }^{2}82°+\cot 24°.\cot 66°+{\cos }^{2}82°.$

Hướng dẫn giải

a) Ta có: $A=\sin 15°-\sin 60°+\cos 30°-\cos 75°+5$

$=\left(\sin 15°-\cos 75°\right)+\left(\cos 30°-\sin 60°\right)+5$

$=\left(\cos 75°-\cos 75°\right)+\left(\cos 30°-\cos 30°\right)+5$

= 0 + 0 + 5 = 5.

b) Ta có: $B={\sin }^{2}82°+\cot 24°.\cot 66°+{\cos }^{2}82°$

$=\left({\sin }^{2}82°+{\cos }^{2}82°\right)+\cot 24°.\cot 66°$

$=1+\tan 66°.\cot 66°$

= 1 + 1 = 2.

Bài 5. Cho tam giác ABC vuông tại A có AC = 10 cm, $\cos A=\frac{1}{2}.$ Tính  sinA và độ dài cạnh AB và BC.

Hướng dẫn giải

Ta có: ${\sin }^{2}A+{\cos }^{2}A=1$ suy ra ${\sin }^{2}A=1-{\cos }^{2}A.$ 

Do đó $\sin A=\sqrt{1-{\cos }^{2}A}.$

• Thay $\cos A=\frac{1}{2},$ ta có: $\sin A=\sqrt{1-{\left(\frac{1}{2}\right)}^2}=\frac{\sqrt{3}}{2}$ (do sin A > 0 vì góc A nhọn).

Ta lại có: $\cos A=\frac{AB}{AC}$ suy ra AB = AC.cos A.

• Thay $\cos A=\frac{1}{2},$ AC = 10 cm, ta có: $AB=10\cdot \frac{1}{2}=5$ (cm).

Mà $\sin A=\frac{BC}{AC}$ suy ra BC = AC.sin A.

• Thay $\sin A=\frac{\sqrt{3}}{2},$ AC = 10 cm, ta có: $BC=10\cdot \frac{\sqrt{3}}{2}=5\sqrt{3}$ (cm)

Vậy $\sin A=\frac{\sqrt{3}}{2},$AB = 5 cm, $BC=5\sqrt{3}$ cm

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Lý thuyết Bài 1: Tỉ số lượng giác của góc nhọn

Lý thuyết Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông

Lý thuyết Bài 1: Đường tròn

Lý thuyết Bài 2: Tiếp tuyến của đường tròn

Lý thuyết Bài 3: Góc ở tâm, góc nội tiếp