Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 1: Căn bậc hai chi tiết sách Toán 9 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 1: Căn bậc hai
Hoạt động khám phá 1 trang 37 Toán 9 Tập 1: Cho trục số được vẽ trên lưới ô vuông đơn vị như Hình 1.
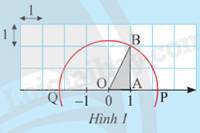
a) Tính độ dài cạnh huyền OB của tam giác vuông OAB.
b) Vẽ đường tròn tâm O bán kính OB, đường tròn này cắt trục số tại hai điểm P và Q.
Gọi x là số thực được biểu diễn bởi điểm P, y là số thực được biểu diễn bởi điểm Q.
Thay mỗi ? bằng số thích hợp để có các đẳng thức:
x2 = ?, y2 = ?.
Lời giải:
a) Áp dụng định lí Pythagore vào tam giác vuông OAB ta có:
OB =
b)
1. Căn bậc hai
Thực hành 1 trang 38 Toán 9 Tập 1: Tính các căn bậc hai của mỗi số sau:
a) 36
b)
c) 1,44
d) 0
Lời giải:
a) Ta có 62 = 36, nên 36 có hai căn bậc hai là 6 và – 6
b) Ta có = , nên có hai căn bậc hai là và -
c) Ta có (1,2)2 = 1,44 nên 1,44 có hai căn bậc hai là 1,2 và – 1,2
d) Số 0 chỉ có một căn bậc hai là chính nó
Thực hành 2 trang 38 Toán 9 Tập 1: Sử dụng dấu căn bậc hai để viết các căn bậc hai của mỗi số:
a) 11
b) 2,5
c) – 0,09
Lời giải:
a) Các căn bậc hai của 11 là và -
b) Các căn bậc hai của 2,5 là và -
c) Do – 0,09 là số âm nên nó không có căn bậc hai.
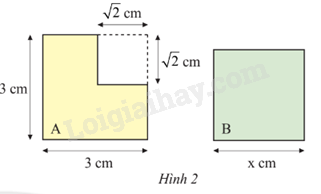
Lời giải:
Xét hình A:
Ta có diện tích cả hình vuông cạnh 3cm là : 3.3 = 9 cm2
Ta có diện tích cả hình vuông cạnh cm là : . = 2 cm2
Suy ra diện tích hình A là: 9 – 2 = 7 cm2
Mà hình vuông B bằng diện tích hình A là 7 cm2
Nên x.x = x2 = 7 suy ra x = cm.
2.Tính căn bậc hai bằng máy tính cầm tay
a)
b)
c)
Lời giải:
a)
b)
c)
Thực hành 6 trang 39 Toán 9 Tập 1: Sử dụng máy tính cầm tay để:
a) Tìm các căn bậc hai của 10,08 (kết quả làm tròn đến chữ số thập phân thứ tư)
b) Tính giá trị của biểu thức (kết quả làm tròn đến chữ số thập phân thứ năm)
Lời giải:
a) Ta có hai căn bậc hai của 10,08 là và
b)
3. Căn thức bậc hai
Hoạt động khám phá 2 trang 40 Toán 9 Tập 1: Một chiếc thang dài 5m tựa vào bức tường như Hình 3.
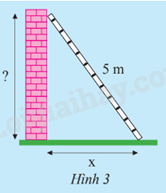
a) Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân tường?
b) Tính độ cao trên khi x nhận giá trị lần lượt là 1; 2; 3; 4.
Lời giải:
a) Đỉnh thang có độ cao là: (m).
b) Khi x = 1 thì độ cao là (m)
Khi x = 2 thì độ cao là (m)
Khi x = 3 thì độ cao là (m)
Khi x = 4 thì độ cao là (m)
Lời giải:
ĐKXĐ: 3x + 6 0 suy ra x - 2
Thay x = 5 vào A = , ta được: A =
Thực hành 8 trang 40 Toán 9 Tập 1: Cho biểu thức P = . Tính giá trị của P khi:
a) a = 5; b = 0
b) a = 5; b = -5
c) a = 2; b = -4
Lời giải:
a) Thay a = 5; b = 0 vào P = , ta được:
P =
b) Thay a = 5; b = -5 vào P = , ta được:
P =
c) Thay a = 2; b = -4 vào P = thì biểu thức P không khác định vì
a2 – b2 = -12 < 0 .
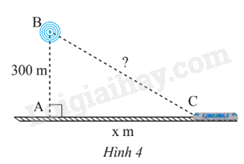
a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.
b) Tính khoảng cách trên khi x = 400; x = 1000 (kết quả làm tròn đến hàng đơn vị của mét).
Lời giải:
a) Ta có khoảng cách từ trạm phát sóng đến đầu tàu là: (m)
b) Thay x = 400 thì khoảng cách từ trạm phát sóng đến đầu tàu là: (m)
Thay x = 1000 thì khoảng cách từ trạm phát sóng đến đầu tàu là: (m)
Bài tập
Đề bài
Bài 1 trang 41 Toán 9 Tập 1: Tìm các căn bậc hai của mỗi số sau:
a) 16
b) 2500
c)
d) 0,09
Lời giải:
a) Ta có 42 = 16, nên 16 có hai căn bậc hai là 4 và – 4
b) Ta có 502 = 2500, nên 2500 có hai căn bậc hai là 50 và – 50
c) Ta có nên có hai căn bậc hai là và –
d) Ta có 0,32 = 0,09 nên 0,09 có hai căn bậc hai là 0,3 và – 0,3.
Bài 2 trang 41 Toán 9 Tập 1: Tính
a)
b)
c)
d)
Lời giải:
a)
b)
c)
d)
Bài 3 trang 41 Toán 9 Tập 1: Biết rằng 252 = 625, tìm các căn bậc hai của các số 625 và 0,0625
Lời giải:
625 có hai căn bậc hai là 25 và – 25
0,0625 có hai căn bậc hai là 0,25 và – 0,25.
a)
b)
c)
Lời giải:
a)
b)
c)
Bài 5 trang 41 Toán 9 Tập 1: Tính giá trị của các biểu thức:
a)
b)
Lời giải:
a)
b)
Bài 6 trang 41 Toán 9 Tập 1: Tìm x, biết:
a) x2 = 121
b) 4x2 = 9
c) x2 = 10
Lời giải:
a) x2 = 121
x2 = 112
b) 4x2 = 9
(2x)2 = 32
c) x2 = 10
Bài 7 trang 41 Toán 9 Tập 1: Tính giá trị của các biểu thức sau khi x = 16; y = 9
a)
b)
c)
d)
Lời giải:
a) Thay x = 16; y = 9, ta được
b) Thay x = 16; y = 9, ta được
c) Thay x = 16; y = 9, ta được
c) Thay x = 16; y = 9, ta được
Bài 8 trang 41 Toán 9 Tập 1: Cho biểu thức P = . Tính giá trị của P khi:
a) x = 3; y = - 2
b) x = 1; y = 4
Lời giải:
a) Thay x = 3; y = - 2 vào P = , ta được: P =
b) Thay x = 1; y = 4 vào P = không xác định vì 12 – 1.4 + 1 = - 2 < 0.
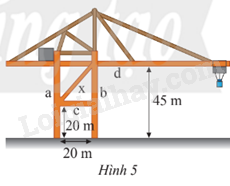
Lời giải:
Nhìn vào hình 5:
Ta có độ dài một cạnh góc vuông là 20 m và cạnh góc vuông còn lại là 45 – 20 = 25 m
x = (m).
Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 3. Tính chất của phép khai phương
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Lý thuyết Căn bậc hai
1. Căn bậc hai
Khái niệm căn bậc hai
|
Cho số thực a không âm. Số thực x thỏa mãn được gọi là một căn bậc hai của a. |
Chú ý:
- Mỗi số dương a có đúng hai căn bậc hai là hai số đối nhau: số dương là (căn bậc hai số học của a) và số âm là .
- Số 0 chỉ có đúng một căn bậc hai là chính nó, ta viết .
- Số âm không có căn bậc hai.
- Phép toán tìm căn bậc hai số học của số không âm gọi là phép khai căn bậc hai hay phép khai phương (gọi tắt là khai phương).
- Nếu thì . Suy ra .
Ví dụ:
2. Tính căn bậc hai của một số bằng máy tính cầm tay
|
Để tính các căn bậc hai của một số , chỉ cần tính . Có thể dễ dàng làm điều này bằng cách sử dụng MTCT.
Sử dụng nút này để bấm căn bậc hai. |
Ví dụ:
Bấm lần lượt các phím  ta tính được .
ta tính được .
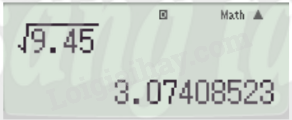
Vậy căn bậc hai của 9,45 (làm tròn đến chữ số thập phân thứ hai) là 3,07 và -3,07.
Tính chất của căn bậc hai
|
với mọi số thực a. |
Ví dụ: ; .
3. Căn thức bậc hai
Khái niệm căn thức bậc hai
|
Với A là một biểu thức đại số, ta gọi là căn thức bậc hai của A, còn A được gọi là biểu thức lấy căn hoặc biểu thức dưới dấu căn. |
Ví dụ: , là các căn thức bậc hai.
Chú ý:
- Ta cũng nói là một biểu thức. Biểu thức xác định (hay có nghĩa) khi A nhận giá trị không âm.
- Khi A nhận giá trị không âm nào đó, khai phương giá trị này ta nhận được giá trị tương ứng của biểu thức .
Ví dụ:
+ Căn thức xác định khi hay .
Tại thì .
+ Giá trị của biểu thức tại là:
.