Với giải sách bài tập Toán 9 Bài 1: Căn bậc hai sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Bài 1: Căn bậc hai

Bài 1 trang 40 sách bài tập Toán 9 Tập 1: Tìm các căn bậc hai của các số:

a) 0,81;

b) $\frac{1}{100};$

c)$1\frac{7}{9};$                  

d) 10⁶.

Lời giải:

a) Ta có 0,9² = 0,81 nên 0,81 có hai căn bậc hai là 0,9 và ‒0,9.

b) Ta có ${\left(\frac{1}{10}\right)}^2=\frac{1}{100}$ nên $\frac{1}{100}$ có hai căn bậc hai là $\frac{1}{10}$ và $\frac{1}{100}$

c) Ta có ${\left(\frac{4}{3}\right)}^2=\frac{16}{9}=1\frac{7}{9},$ nên $1\frac{7}{9}$ có hai căn bậc hai là $\frac{4}{3}$ và $-\frac{4}{3}.$

d) Ta có (10³)² = 10⁶ nên 10⁶ có hai căn bậc hai là 10³ = 1 000 và ‒10³ = ‒1 000.

Bài 2 trang 40 sách bài tập Toán 9 Tập 1: Tìm số có căn bậc hai là:

a) $\sqrt{6};$

b) 0,5;

c) $-\sqrt{16};$

d) $-\frac{1}{2}.$

Lời giải:

a) Ta có: ${\left(\sqrt{6}\right)}^2=6$

Vậy số có căn bậc hai là $\sqrt{6}$ là 6.

b) Ta có: 0,5² = 0,25

Vậy số có căn bậc hai là 0,5 là 0,25.

c) Ta có: ${\left(-\sqrt{16}\right)}^2=16$

Vậy số có căn bậc hai là $-\sqrt{16}$ là 16.

d) Ta có: ${\left(-\frac{1}{2}\right)}^2=\frac{1}{4}$

Vậy số có căn bậc hai là $-\frac{1}{2}$ là $\frac{1}{4}.$

Bài 3 trang 40 sách bài tập Toán 9 Tập 1: Tìm x, biết:

a) x² = 64;

b) 9x² = 1;

c) 4x² = 25.

Lời giải:

a) x² = 64

    x² = 8² = (‒8)²

    x = 8 hoặc x = ‒8.

Vậy x ∈ {8; ‒8}.

b) 9x² = 1

$x^2=\frac{1}{9}$

$x^2={\left(\frac{1}{3}\right)}^2={\left(-\frac{1}{3}\right)}^2$

$x=\frac{1}{3}$ hoặc $x=-\frac{1}{3}.$

Vậy $x\in \left\{\frac{1}{3};-\frac{1}{3}\right\}.$

c) 4x² = 25

$x^2=\frac{25}{4}$

$x^2={\left(\frac{5}{2}\right)}^2={\left(-\frac{5}{2}\right)}^2$

$x=\frac{5}{2}$ hoặc $x=-\frac{5}{2}.$

Vậy $x\in \left\{\frac{5}{2};-\frac{5}{2}\right\}.$

Bài 4 trang 40 sách bài tập Toán 9 Tập 1: Tìm x, biết:

a) $\sqrt{x}=9;$

b) $\sqrt{x}=\sqrt{5};$

c) $3\sqrt{x}=1$

d) $2\sqrt{x+1}=12.$

Lời giải:

a) 

x = 81.

Vậy x = 81.

b) $\sqrt{x}=\sqrt{5}$

${\left(\sqrt{x}\right)}^2={\left(\sqrt{5}\right)}^2$

x = 5.

Vậy x = 5.

c) $3\sqrt{x}=1$

${\left(3\sqrt{x}\right)}^2=1^2$

9x = 1

$x=\frac{1}{9}$

Vậy $x=\frac{1}{9}$

d) $2\sqrt{x+1}=12$

${\left(2\sqrt{x+1}\right)}^2={12}^2$

4(x+1) = 144

x + 1 = 36

x = 35.

Vậy x = 35.

Bài 5 trang 41 sách bài tập Toán 9 Tập 1: Tính giá trị của các biểu thức:

a) ${\left(\sqrt{18}\right)}^2+{\left(-\sqrt{12}\right)}^2;$

b) $\sqrt{{\left(-10\right)}^2}-\sqrt{144};$

c) $\sqrt{9^2}\cdot {\left(-\sqrt{6}\right)}^2;$

d) $\sqrt{\mathrm{0,16}}:{\left(-\sqrt{4}\right)}^2.$

Lời giải:

a) ${\left(\sqrt{18}\right)}^2+{\left(-\sqrt{12}\right)}^2=18+12=30.$

b) $\sqrt{{\left(-10\right)}^2}-\sqrt{144}=10-\sqrt{{12}^2}=10-12=-2.$

c) $\sqrt{9^2}\cdot {\left(-\sqrt{6}\right)}^2=9\cdot 6=54.$

d) $\sqrt{\mathrm{0,16}}:{\left(-\sqrt{4}\right)}^2=\sqrt{{\mathrm{0,4}}^2}:4=\mathrm{0,4}:4=\mathrm{0,1.}$

Bài 6 trang 41 sách bài tập Toán 9 Tập 1: Tính giá trị của các biểu thức:

a) $A=\sqrt{144}-{\left(-\sqrt{11}\right)}^2+4\cdot {\left(\sqrt{\frac{7}{2}}\right)}^2-{\left(-\sqrt{3}\right)}^4;$

b) $B={\left(-\sqrt{12}\right)}^2:\sqrt{16}-\sqrt{\frac{1}{49}}\cdot {\left(\sqrt{7}\right)}^2.$

Lời giải:

a) $A=\sqrt{{12}^2}-11+4\cdot \frac{7}{2}-{\left[{\left(-\sqrt{3}\right)}^2\right]}^2$$=12-11+14-3^2=12-11+14-9=6;$

b) $B=12:\sqrt{4^2}-\sqrt{{\left(\frac{1}{7}\right)}^2}\cdot 7$$=12:4-\frac{1}{7}\cdot 7=3-1=2.$

Bài 7 trang 41 sách bài tập Toán 9 Tập 1: So sánh các cặp số sau:

a) $\sqrt{3}$ và $\sqrt{\frac{5}{2}};$

b) 4 và $\sqrt{15}.$

Lời giải:

a) Ta có: $3=\frac{6}{2}>\frac{5}{2}$ nên $\sqrt{3}>\sqrt{\frac{5}{2}}.$

b) Ta có: 16 > 15 nên $\sqrt{16}>\sqrt{15}$ hay $4>\sqrt{15}.$

Bài 8 trang 41 sách bài tập Toán 9 Tập 1: Sắp xếp các số sau theo thứ tự từ nhỏ đến lớn.

$\frac{1}{5};-\sqrt{3};-\sqrt{\frac{3}{2}};\sqrt{5}.$

Lời giải:

– Ta chia các số trên thành hai nhóm:

+ Nhóm 1: gồm hai số $-\sqrt{3}$ và $-\sqrt{\frac{3}{2}};$

+ Nhóm 2: gồm hai số $\frac{1}{5}$ và $\sqrt{5}.$

– So sánh các số trong nhóm 1: $-\sqrt{3}$ và $-\sqrt{\frac{3}{2}};$

Ta có: $3=\frac{6}{2}>\frac{3}{2}$ nên $\sqrt{3}>\sqrt{\frac{3}{2}},$ suy ra $-\sqrt{3}<-\sqrt{\frac{3}{2}}.$

– So sánh các số trong nhóm 2: $\frac{1}{5}$ và $\sqrt{5}.$

Ta có: $\frac{1}{25}<5$ nên $\sqrt{\frac{1}{25}}<\sqrt{5}$

Mà $\sqrt{\frac{1}{25}}=\sqrt{{\left(\frac{1}{5}\right)}^2}=\frac{1}{5},$ suy ra $\frac{1}{5}<\sqrt{5}.$

Mặt khác, các số trong nhóm 1 là các số âm và các số trong nhóm 2 là các số dương. Do vậy, ta có: $-\sqrt{3}<-\sqrt{\frac{3}{2}}<\frac{1}{5}<\sqrt{5}.$

Vậy sắp xếp các số đã cho theo thứ tự từ nhỏ đến lớn như sau:

$-\sqrt{3};-\sqrt{\frac{3}{2}};\frac{1}{5};\sqrt{5}.$

Bài 9 trang 41 sách bài tập Toán 9 Tập 1: Tìm x để căn thức xác định:

a) $\sqrt{2x+7};$

b) $\sqrt{12-3x};$

c) $\sqrt{\frac{1}{x-4}};$

d) $\sqrt{x^2+1}.$

Lời giải:

a) Biểu thức $\sqrt{2x+7}$ xác định khi 2x + 7 ≥ 0 hay 2x ≥ ‒7, hay $x\ge -\frac{7}{2}.$

b) Biểu thức $\sqrt{12-3x}$ xác định khi 12 ‒ 3x ≥ 0 hay ‒3x ≥ ‒12, hay x ≤ 4.

c) Biểu thức $\sqrt{\frac{1}{x-4}}$ xác định khi $\frac{1}{x-4}\ge 0$ hay x ‒ 4 > 0 (do 1 > 0), hay x > 4.

d) Với mọi x ∈ ℝ, ta luôn có x² ≥ 0, do đó x² + 1 ≥ 1 hay x² + 1 > 0.

Suy ra căn thức $\sqrt{x^2+1}$ xác định với mọi số thực x.

Bài 10 trang 41 sách bài tập Toán 9 Tập 1: Tìm giá trị của biểu thức $A=\sqrt{a^2+9a}$ khi a = 16.

Lời giải:

Với a = 16, ta có a² + 9a = 16² + 9.16 = 256 + 144 = 400.

Khi đó, $A=\sqrt{400}=\sqrt{{20}^2}=20.$

Bài 11 trang 41 sách bài tập Toán 9 Tập 1: Diện tích S của hình tròn bán kính r được tính theo công thức S = πr².

a) Viết công thức tính bán kính r theo diện tích S của hình tròn.

b) Tính bán kính r (cm) của hình tròn có diện tích 20 cm² (kết quả làm tròn đến hàng phần mười của xăngtimét).

Lời giải:

a) Từ S = πr², ta có $r^2=\frac{S}{\pi },$ suy ra $r=\sqrt{\frac{S}{\pi }}$ (do r > 0).

Vậy công thức tính bán kính r theo diện tích S của hình tròn là $r=\sqrt{\frac{S}{\pi }}$

b) Với S = 20 cm², ta có $r=\sqrt{\frac{20}{\pi }}\approx \mathrm{2,5}$ (cm).

Bài 12 trang 41 sách bài tập Toán 9 Tập 1: Thời gian rơi t tính theo giây của một vật được thả rơi tự do từ độ cao h (m) cho đến khi chạm đất thoả mãn hệ thức h = 5t².

a) Tính thời gian rơi của vật khi h = 20 m và khi h = 10 m (kết quả làm tròn đến hàng phần mười của giây).

b) Viết công thức biểu thị thời gian rơi t theo độ cao h (h > 0).

Lời giải:

a) Với h = 20 m, ta có 20 = 5t² hay t² = 4, suy ra t = 2 (giây) (do t > 0).

Với h = 10 m, ta có 10 = 5t² hay t² = 2 suy ra $t=\sqrt{2}\approx \mathrm{1,4}$(giây) (do t > 0).

b) Từ h = 5t², suy ra $t^2=\frac{h}{5},$ suy ra $t=\sqrt{\frac{h}{5}}$ (do t > 0).

Vậy công thức biểu thị thời gian rơi t theo độ cao h (h > 0) là: $t=\sqrt{\frac{h}{5}}.$

Bài 13 trang 41 sách bài tập Toán 9 Tập 1: Cho hình chữ nhật ABCD có diện tích bằng 10 cm² và tỉ số giữa hai cạnh kề nhau AB : AD = 3 : 2. Tìm độ dài cạnh AB (kết quả làm tròn đến hàng phần mười của xăngtimét).

Lời giải:

Đặt AB = x (cm) (x > 0).

Ta có $\frac{AB}{AD}=\frac{3}{2},$ suy ra $AD=\frac{2AB}{3}=\frac{2x}{3}\text{ (cm).}$

Diện tích hình chữ nhật ABCD là $S=AB\cdot AD=x\cdot \frac{2x}{3}=\frac{2x^2}{3}$ (cm²).

Theo đề bài, hình chữ nhật ABCD có diện tích bằng 10 cm² nên ta có:

$\frac{2x^2}{3}=\mathrm{10,}$ suy ra x² = 15, suy ra $x=\sqrt{15}\approx \mathrm{3,9}$ (cm) (do x > 0).

Vậy độ dài cạnh AB là khoảng 3,9 cm.

Bài 14 trang 41 sách bài tập Toán 9 Tập 1: Tìm tất cả các số tự nhiên n sao cho $\sqrt{9-n}$ là số tự nhiên.

Lời giải:

⦁ Điều kiện xác định của căn thức $\sqrt{9-n}$ là 9 ‒ n ≥ 0 hay n ≤ 9.

⦁ Vì n là số tự nhiên nên n ≥ 0, suy ra ‒ n ≤ 0, do đó 9 ‒ n ≤ 9.

Suy ra 0 ≤ 9 ‒ n ≤ 9.

⦁ Như vậy, để A = $\sqrt{9-n}$ là số tự nhiên thì 9 ‒ n phải nhận các giá trị là số chính phương.

Do đó 9 ‒ n ∈ {0; 1; 4; 9}.

Ta có bảng sau:

Vậy các giá trị cần tìm của n là 9; 8; 5; 0.

Lý thuyết Căn bậc hai

1. Căn bậc hai

Khái niệm căn bậc hai

Chú ý:

- Mỗi số dương a có đúng hai căn bậc hai là hai số đối nhau: số dương là $\sqrt{a}$ (căn bậc hai số học của a) và số âm là $-\sqrt{a}$.

- Số 0 chỉ có đúng một căn bậc hai là chính nó, ta viết $\sqrt{0}=0$.

- Số âm không có căn bậc hai.

- Phép toán tìm căn bậc hai số học của số không âm gọi là phép khai căn bậc hai hay phép khai phương (gọi tắt là khai phương).

­- Nếu $a>b>0$ thì $\sqrt{a}>\sqrt{b}$. Suy ra $-\sqrt{a}<-\sqrt{b}<0<\sqrt{b}<\sqrt{a}$.

Ví dụ:

• $\sqrt{81}=9$ nên 81 có hai căn bậc hai là 9 và -9.
• Căn bậc hai số học của 121 là $\sqrt{121}=11$.

2. Tính căn bậc hai của một số bằng máy tính cầm tay

Ví dụ:

Bấm lần lượt các phím  ta tính được $\sqrt{9,45}\approx 3,07$.

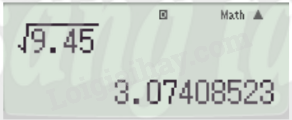
Vậy căn bậc hai của 9,45 (làm tròn đến chữ số thập phân thứ hai) là 3,07 và -3,07.

Tính chất của căn bậc hai

Ví dụ: $\sqrt{{\left(1+\sqrt{2}\right)}^2}=\left|1+\sqrt{2}\right|=1+\sqrt{2}$; $\sqrt{{\left(-3\right)}^2}=\left|-3\right|=3$.

3. Căn thức bậc hai

Khái niệm căn thức bậc hai

Ví dụ: $\sqrt{2x-1}$, $\sqrt{-\frac{1}{3}x+2}$ là các căn thức bậc hai.

Chú ý:

- Ta cũng nói $\sqrt{A}$ là một biểu thức. Biểu thức $\sqrt{A}$ xác định (hay có nghĩa) khi A nhận giá trị không âm.

- Khi A nhận giá trị không âm nào đó, khai phương giá trị này ta nhận được giá trị tương ứng của biểu thức $\sqrt{A}$.

Ví dụ:

+ Căn thức $\sqrt{2x+1}$ xác định khi $2x+1\ge 0$ hay $x\ge -\frac{1}{2}$.

Tại $x=4$ thì $\sqrt{2.4+1}=\sqrt{9}=\sqrt{3^2}=3$.

+ Giá trị của biểu thức $\sqrt{b^2-4ac}$ tại $a=3;b=10;c=3$ là:

  $\sqrt{{10}^2-\mathrm{4.3.3}}=\sqrt{100-36}=\sqrt{64}=\sqrt{8^2}=8$.

Xem thêm các bài giải SBT Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 2

Bài 1: Căn bậc hai

Bài 2: Căn bậc ba

Bài 3: Tính chất của phép khai phương

Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Bài tập cuối chương 3