Với giải HĐ3 trang 29 Chuyên đề Toán 12 Kết nối tri thức chi tiết trong Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 12. Mời các bạn đón xem:

Giải Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính

HĐ3 trang 29 Chuyên đề Toán 12: Xét bài toán quy hoạch tuyến tính F(x; y) = 3x + 4y → min

với các ràng buộc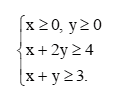 

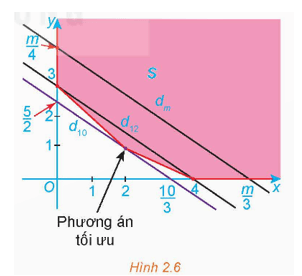
a) Kiểm tra lại rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán.

b) Tìm tập hợp các điểm M(x; y) thoả mãn F(x; y) = 3x + 4y = 12.

c) Với mỗi số thực m, xét đường thẳng d_m: 3x + 4y = m.

Từ hình vẽ, tìm điều kiện của m để d_m ∩ S ≠ ∅.

d) Từ phần c suy ra giá trị nhỏ nhất của F(x; y) trên miền chấp nhận được. Chứng tỏ rằng, giá trị nhỏ nhất này chính là giá trị của F(x; y) tại một điểm cực biên của miền chấp nhận được.

Lời giải:

a) Biểu diễn miền nghiệm của các bất phương trình trong hệ ràng buộc ta thấy rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán.

b) Theo bài, F(x; y) = 3x + 4y = 12.

Vậy tập hợp điểm M(x; y) thỏa mãn yêu cầu đề bài là tập hợp các điểm nằm trên đường thẳng d₁₂: 3x + 4y = 12 nằm trong miền chấp nhận S, chính là tập hợp các điểm nằm trên đoạn thẳng AB (hình vẽ).

b) Đường thẳng d_m song song với AB, có phương không đổi, do đó từ hình vẽ, ta thấy đường thẳng d_m: 3x + 4y = m luôn cắt trục tung tại điểm có tung độ $y=\frac{m}{4}.$

Từ hình vẽ, ta thấy rằng để d_m ∩ S ≠ ∅ thì $\frac{m}{4}\ge \frac{5}{2},$ tức là m ≥ 10.

Vậy m ≥ 10.

c) Ta có: F(x; y) = 3x + 4y = m, mà theo kết quả của câu b, ta có m ≥ 10 nên F(x; y) ≥ 10.

Vậy giá trị nhỏ nhất của F(x; y) trên miền S là 10.

Ta có các điểm cực biên của miền S là: (0; 3), (2; 1), (4; 0).

⦁ F(0; 3) = 3.0 + 4.3 = 12;

⦁ F(2; 1) = 3.2 + 4.1 = 10;

⦁ F(4; 0) = 3.4 + 4.0 = 12.

Vậy giá trị nhỏ nhất của F(x; y) trên miền S chính là giá trị của F(x; y) tại điểm cực biên có tọa độ (2; 1) của miền chấp nhận được.