Bài 4.3 trang 62 Toán lớp 7: Tính các số đo x, y, z trong Hình 4.8

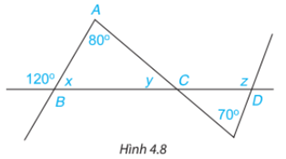
Phương pháp giải:

Lời giải:

Ta có

$x+{120}^o={180}^o$(kề bù)

$\begin{array}{l}\Rightarrow x={180}^o-{120}^o\\ \Rightarrow x={60}^o\end{array}$

Xét tam giác ABC có:

$\begin{array}{l}\hat{A}+\hat{B}+\hat{C}={180}^o\\ \Rightarrow {80}^o+{60}^o+y={180}^o\\ \Rightarrow y={40}^o\end{array}$

Ta có: $\widehat{DCE}=y={40}^o$(đối đỉnh)

$\begin{array}{l}\hat{C}+\hat{D}+\hat{E}={180}^O\\ \Rightarrow {40}^o+\hat{D}+{70}^o={180}^o\\ \Rightarrow \hat{D}={70}^o\\ \hat{D}+z={180}^o\\ \Rightarrow z={180}^o-{70}^o={110}^o\end{array}$

$\begin{array}{l}\hat{C}+\hat{D}+\hat{E}={180}^O\\ \Rightarrow {40}^o+\hat{D}+{70}^o={180}^o\\ \Rightarrow \hat{D}={70}^o\end{array}$

Mà $\hat{D}+z={180}^o$( 2 góc kề bù)

$\Rightarrow z={180}^o-{70}^o={110}^o$

Bài tập vận dụng:

Bài 1. Tính số đo x trong các hình dưới đây:

Hướng dẫn giải

a) Tam giác ABC có: $\hat{A}+\hat{B}+\hat{C}=180°$ (tổng ba góc trong tam giác)

Do đó: $40°+70°+x=180°$

$x=180°-40°-70°$

$x=70°$

Vậy $x=70°$

b) Tam giác DGE có: $\hat{D}+\hat{G}+\hat{E}=180°$ (tổng ba góc trong tam giác)

Do đó: $90°+60°+x=180°$

$x=180°-90°-60°$

$x=30°$

Vậy $x=30°$

c) Tam giác IJK có: $\hat{I}+\hat{J}+\hat{K}=180°$ (tổng ba góc trong tam giác)

Do đó: $50°+x+x=180°$

$x+x=180°-50°$

$2x=130°$

$x=65°$

Vậy $x=65°$

Bài 2. Tính số đo a; b; c trong các hình dưới đây:

Hướng dẫn giải

Ta có: $\widehat{PKt}=\widehat{PQK}+\widehat{QPK}$ (góc ngoài của tam giác)

Do đó: $145°=83°+a$

$a=145°-83°=62°$

Ta có: $\widehat{MPN}=\widehat{QPK}$ (hai góc đối đỉnh)

Do đó: $\widehat{MPN}=a=62°$

Có: $\widehat{NMP}+\widehat{MPN}+\widehat{PNM}=180°$ (tổng ba góc trong tam giác)

Do đó: $b+62°+72°=180°$

$b=180°-62°-72°=46°$

Có: $\widehat{zMP}+\widehat{NMP}=180°$ (hai góc kề bù)

Do đó: $c+b=180°$

$c+46°=180°$

$c=180°-46°=134°$

Vậy $a=62°$; $b=46°$; $c=134°$.

Bài 3. Trong các tam giác dưới đây. Tam giác nào là tam giác nhọn, tam giác vuông, tam giác tù?

Hướng dẫn giải

a) Tam giác MLN có: $\hat{M}+\hat{L}+\hat{N}=180°$ (tổng ba góc trong tam giác)

Do đó: $53°+\hat{L}+37°=180°$⟹$\hat{L}=180°-53°-37°=90°$

Như vậy góc L là góc vuông nên tam giác MLN là tam giác vuông.

b) Tam giác POQ có: $\hat{P}+\hat{O}+\hat{Q}=180°$ (tổng ba góc trong tam giác)

Do đó: $82°+54°+\hat{Q}=180°$⟹$\hat{Q}=180°-82°-54°=44°$< 90°

Như vậy góc Q; góc O; góc P là góc nhọn nên tam giác POQ là tam giác nhọn.

c) Tam giác SRT có: $\hat{S}+\hat{R}+\hat{T}=180°$ (tổng ba góc trong tam giác)

Do đó: $27°+\hat{R}+33°=180°$⟹$\hat{R}=180°-27°-33°=120°$> 90°

Như vậy góc R là góc tù nên tam giác SRT là tam giác tù.