Với giải Luyện tập 2 trang 81 Toán lớp 7 Kết nối tri thức chi tiết trong Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
Luyện tập 2 trang 81 Toán lớp 7: a) Chứng minh trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Phương pháp giải:
a) Chứng minh A thuộc đường trung trực BC nên AD là đường cao.
Chứng minh: từ đó suy ra AD là phân giác góc A
b) Điểm cách đều ba đỉnh là giao của ba đường trung trực trong tam giác GA = GB = GC
Sử dụng kết quả ý a, chứng minh G là giao điểm ba đường phân giác trong tam giác ABC
Lời giải:
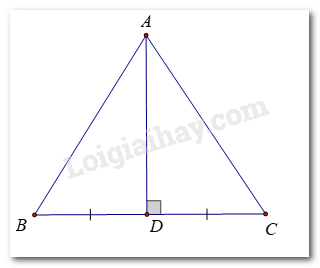
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
thuộc đường trung trực của cạnh BC (t/c)
là đường trung trực của BC.
Xét và có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
AD là tia phân giác góc BAC.
Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
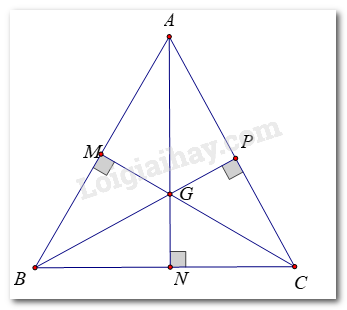
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
là giao điểm ba đường phân giác của tam giác ABC
cách đều ba cạnh của tam giác ABC (Tính chất)
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Câu hỏi trang 77 Toán lớp 7: Mỗi tam giác có mấy đường trung trực...
Vận dụng 1 trang 79 Toán lớp 7: Em hãy trả lời câu hỏi trong tình huống mở đầu...
Câu hỏi trang 79 Toán lớp 7: Mỗi tam giác có mấy đường cao?...
Bài 9.27 trang 81 Toán lớp 7: Cho tam giác ABC có và trực tâm H. Tìm góc BHC...
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác