Với giải Bài 5.23 trang 103 Toán 9 Tập 1 Kết nối tri thức chi tiết trong Bài 16: Vị trí tương đối của đường thẳng và đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn
Bài 5.23 trang 103 Toán 9 Tập 1: Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.
a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB.
b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF.
Lời giải:
a)
Hai tiếp tuyến EM và EA cắt nhau tại E nên EM = EA.
Hai tiếp tuyến FM và EB cắt nhau tại F nên FM = FB.
Chu vi tam giác SEF là:
CSEF = SE + SF + EF = SE + SF + EM + MF
= SE + EA + SF + BF = SA + SB.
Vậy chu vi của tam giác SEF bằng SA + SB.
b)
Vì SA và SB là hai tiếp tuyến cắt nhau tại S nên SO là phân giác của .
Suy ra hay .
Xét ΔSME và ΔSMF có:
SM chung
Do đó ΔSME = ΔSMF (g.c.g)
Suy ra SE = SF (hai cạnh tương ứng).
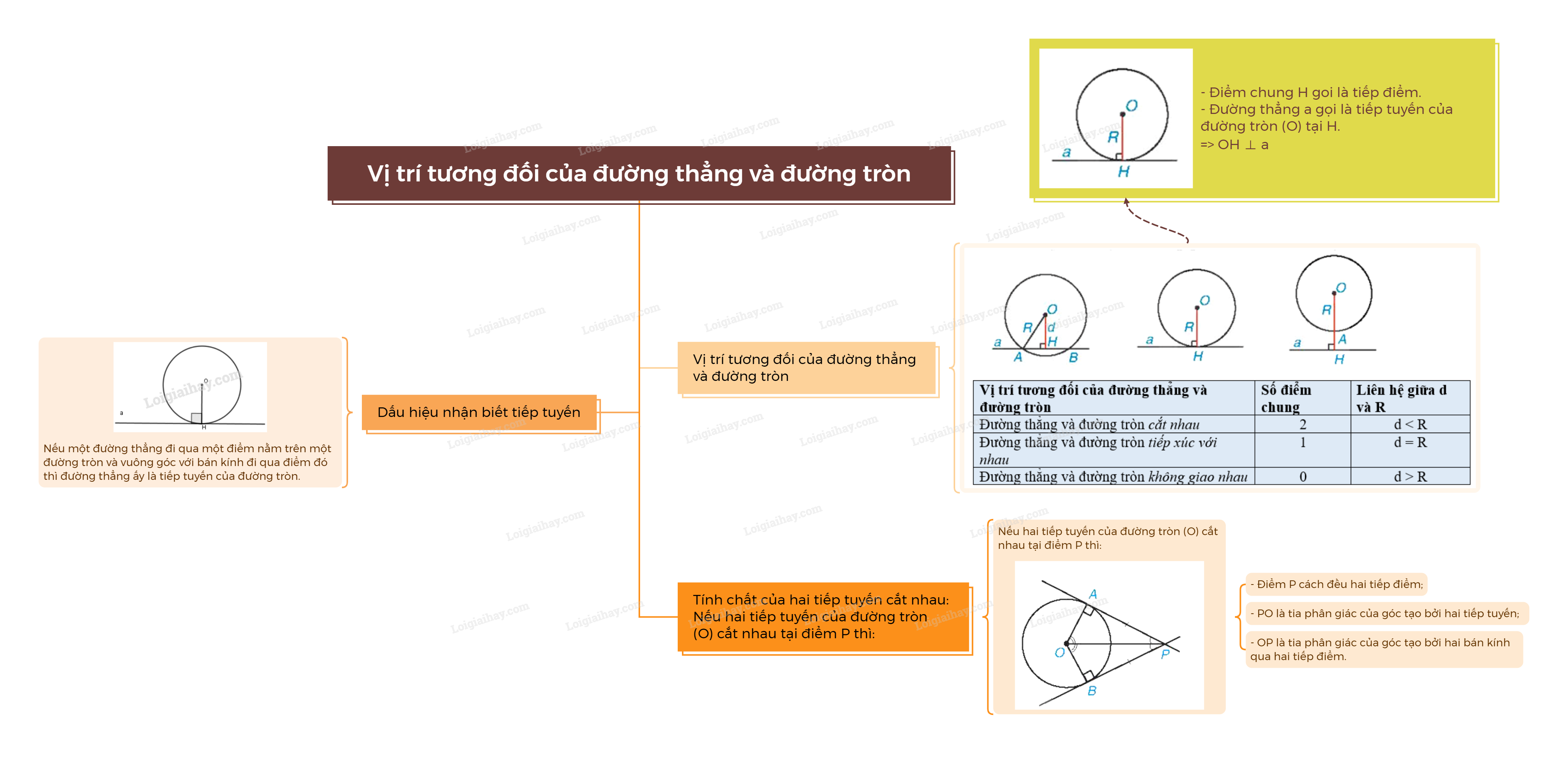
Sơ đồ tư duy Vị trí tương đối của đường thẳng và đường tròn
Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:
HĐ2 trang 100 Toán 9 Tập 1: Cho đoạn thẳng OH và đường thẳng a vuông góc với OH tại H........
Xem thêm các bài giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:
Bài 16. Vị trí tương đối của đường thẳng và đường tròn
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
