Với giải HĐ4 trang 102 Toán 9 Tập 1 Kết nối tri thức chi tiết trong Bài 16: Vị trí tương đối của đường thẳng và đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn
HĐ4 trang 102 Toán 9 Tập 1: (Dựa vào hình vẽ có được sau HĐ3). Bằng cách xét hai tam giác OMA và OMB, chứng minh rằng:
a) MA = MB;
b) MO là tia phân giác của góc AMB;
c) OM là tia phân giác của góc AOB.
Lời giải:
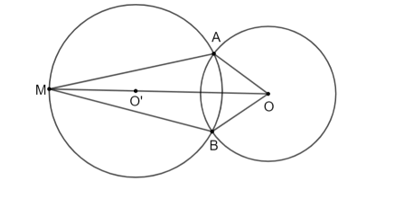
a) Xét hai tam giác vuông OAM và OBM có:
OA = OB; OM chung
Do đó ΔOAM = ΔOBM (cạnh huyền – cạnh góc vuông).
Suy ra AM = BM (hai cạnh tương ứng).
b) Vì ΔOAM = ΔOBM (câu a) nên (hai góc tương ứng).
Suy ra OM là tia phân giác của góc AMB.
c) Vì ΔOAM = ΔOBM (câu a) nên (hai góc tương ứng).
Suy ra Om là tia phân giác của góc AOB.
Lý Thuyết Hai tiếp tuyến cắt nhau của một đường tròn
Tính chất của hai tiếp tuyến cắt nhau
|
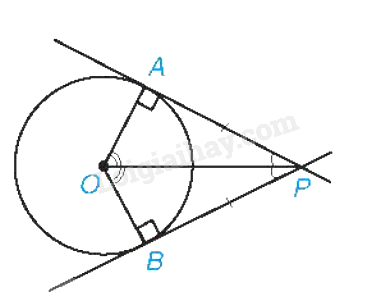
Nếu hai tiếp tuyến của đường tròn (O) cắt nhau tại điểm P thì:
- Điểm P cách đều hai tiếp điểm;
- PO là tia phân giác của góc tạo bởi hai tiếp tuyến;
- OP là tia phân giác của góc tạo bởi hai bán kính qua hai tiếp điểm.
|
Ví dụ: Cho đường tròn (O), B, C (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.
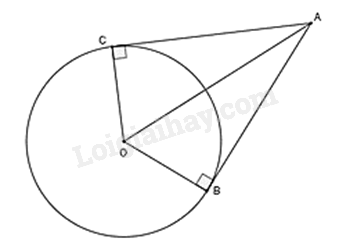
Khi đó:
- AB = AC
- Tia AO là tia phân giác của .
- Tia OA là tia phân giác của .
Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:
Mở đầu trang 99 Toán 9 Tập 1: Người ta gieo một đồng xu hình tròn bán kính 1 cm lên một tờ giấy trải phẳng. Trên tờ giấy đó có vẽ những đường thẳng song song cách đều, tức là những đường thẳng song song mà khoảng cách giữa hai đường thẳng bất kì nằm cạnh nhau luôn bằng nhau. Nếu khoảng cách ấy luôn bằng 2 cm thì có thể xảy ra những trường hợp nào sau đây, vì sao?.......
HĐ1 trang 99 Toán 9 Tập 1: Cho đường thẳng a và điểm O. Gọi H là chân đường vuông góc hạ từ O xuống a, và A là một điểm thuộc tia OH. Trong mỗi trường hợp sau đây, hãy vẽ đường tròn (O; OA) và cho biết đường thẳng a và đường tròn (O; OA) có bao nhiêu điểm chung?.......
Luyện tập 1 trang 100 Toán 9 Tập 1: Cho đường thẳng a và điểm O cách a một khoảng bằng 4 cm. Không vẽ hình, hãy dự đoán xem mỗi đường tròn sau cắt, tiếp xúc hay không cắt đường thẳng a. Tại sao?......
HĐ2 trang 100 Toán 9 Tập 1: Cho đoạn thẳng OH và đường thẳng a vuông góc với OH tại H........
Luyện tập 2 trang 101 Toán 9 Tập 1: Cho một hình vuông có độ dài mỗi cạnh bằng 6 cm và hai đường chéo cắt nhau tại I. Chứng minh rằng đường tròn (I; 3 cm) tiếp xúc với cả bốn cạnh của hình vuông.......
Thực hành trang 101 Toán 9 Tập 1: Cho đường thẳng a và điểm M không thuộc a. Hãy vẽ đường tròn tâm M tiếp xúc với a.......
Vận dụng trang 101 Toán 9 Tập 1: Trở lại tình huống mở đầu. Ở đây, ta hiểu đồng xu nằm đè lên một đường thẳng khi đường tròn (hình ảnh của đồng xu) và đường thẳng ấy cắt nhau.......
HĐ3 trang 101 Toán 9 Tập 1: Cho điểm M ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau:......
HĐ4 trang 102 Toán 9 Tập 1: (Dựa vào hình vẽ có được sau HĐ3). Bằng cách xét hai tam giác OMA và OMB, chứng minh rằng:......
Thử thách nhỏ trang 103 Toán 9 Tập 1: Cho góc xMy và điểm A thuộc tia Mx. Hãy vẽ đường tròn tâm O tiếp xúc với cả hai cạnh của góc xMy sao cho A là một trong hai tiếp điểm.......
Bài 5.20 trang 103 Toán 9 Tập 1: Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 6 cm). Hỏi nếu bạn Thanh dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b thì hình nào đè lên đường thẳng a, hình nào không đè lên đường thẳng a?.......
Bài 5.21 trang 103 Toán 9 Tập 1: Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O)........
Bài 5.22 trang 103 Toán 9 Tập 1: Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).......
Bài 5.23 trang 103 Toán 9 Tập 1: Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F......
Xem thêm các bài giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:
Luyện tập chung trang 96
Bài 16. Vị trí tương đối của đường thẳng và đường tròn
Bài 17. Vị trí tương đối của hai đường tròn
Luyện tập chung trang 108
Bài tập cuối chương 5
Pha chế dung dịch theo nồng độ yêu cầu

