Với giải Luyện tập 2 trang 102 Toán 9 Tập 1 Cánh diều chi tiết trong Bài 2: Vị trí tương đối của đường thẳng và đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn

Luyện tập 2 trang 102 Toán 9 Tập 1: Cho tam giác ABC vuông tại A, AB = 3 cm, BC = 5 cm. Đường thẳng AB có tiếp xúc với đường tròn (C; 4 cm) hay không? Vì sao?

Lời giải:

Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:

BC² = AB² + AC²

Suy ra AC² = BC² – AB² = 5² – 3² = 16.

Do đó AC = 4 cm (do AC > 0).

Vì CA ⊥ AB tại A nên khoảng cách từ điểm C đến đường thẳng AB bằng CA.

Mà AC = 4 cm nên khoảng cách từ tâm C của đường tròn (C; 4 cm) đến đường thẳng AB bằng bán kính của đường tròn.

Vậy đường thẳng AB tiếp xúc với đường tròn (C; 4 cm).

Lý thuyết Đường thẳng và đường tròn tiếp xúc nhau

Nếu đường thẳng và đường tròn tiếp xúc nhau thì đường thẳng được gọi là tiếp tuyến của đường tròn, điểm chung được gọi là tiếp điểm.

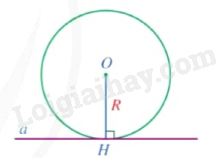
Nhận xét: Đường thẳng a tiếp xúc với đường tròn (O;R) khi khoảng cách từ tâm O đến đường thẳng a bằng R và ngược lại.