Với lời giải Toán 11 trang 64 Tập 2 chi tiết trong Bài 2: Đường thẳng vuông góc với mặt phẳng sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng

Thực hành 5 trang 64 Toán 11 Tập 2: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Vẽ đường thẳng qua O và vuông góc với (ABC) tại H. Chứng minh AH ⊥ BC.

Lời giải:

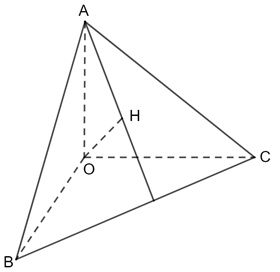
Ta có: $\left\{\begin{array}{l}\mathrm{OA}\perp \mathrm{OB}\\ \mathrm{OA}\perp \mathrm{OC}\end{array}\right.$

⇒ $\mathrm{OA}\perp \left(\mathrm{OBC}\right)\Rightarrow \mathrm{OA}\perp \mathrm{BC}$ (1)

Mà $\mathrm{OH}\perp \left(\mathrm{ABC}\right)\Rightarrow \mathrm{OH}\perp \mathrm{BC}$ (2)

Từ (1) và (2) ⇒ $\Rightarrow \mathrm{BC}\perp \left(\mathrm{OAH}\right)\Rightarrow \mathrm{BC}\perp \mathrm{AH}(\mathrm{AH}\subset \left(\mathrm{OAH}\right)$ .

Vận dụng 3 trang 64 Toán 11 Tập 2: Nêu cách tìm hình chiếu vuông góc của một đoạn thẳng AB trên trần nhà xuống nền nhà bằng hai dây dọi.

Lời giải:

Thả dây dọi từ điểm A và đánh dấu điểm A′ nơi đầu quả dọi chạm sàn.

Thả dây dọi từ điểm B và đánh dấu điểm B′ nơi đầu quả dọi chạm sàn.

Khi đó đoạn thẳng A′B′ là hình chiếu vuông góc của một đoạn thẳng AB trên trần nhà xuống nền nhà.

Bài tập

Bài 1 trang 64 Toán 11 Tập 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD). Cho biết ABCD là hình thang vuông tại A và D, AB = 2AD.

a) Chứng minh CD ⊥ (SAD) .

b) Gọi M là trung điểm của AB . Chứng minh CM ⊥ (SAB) .

Lời giải:

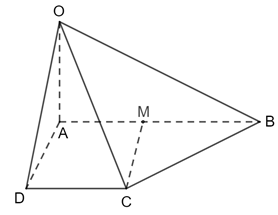
a) Ta có:

$\left.\begin{array}{c}\mathrm{SA}\perp \left(\text{ABCD}\right)\Rightarrow \mathrm{SA} \perp \mathrm{CD}\\ \mathrm{AD}\perp \mathrm{CD}\end{array}\right\}\Rightarrow \text{CD}\perp \left(\text{SAD}\right)$

b) Ta có:

AB // CD ⇒ AM // CD

AM = CD $\left(=\frac{1}{2}\mathrm{AB}\right)$

⇒ AMCD là hình bình hành

Mà $\widehat{\mathrm{MAD}}=90°$ ⇒ AMCD là hình chữ nhật.

$\left.\begin{array}{c}\Rightarrow \mathrm{CM} \perp \mathrm{AB}\\ \mathrm{SA} \perp \left(\mathrm{ABCD}\right)\Rightarrow \mathrm{SA}\perp \mathrm{CM}\end{array}\right\}\Rightarrow \text{CM}\perp \left(\text{SAB}\right)$

Bài 2 trang 64 Toán 11 Tập 2: Cho hình vuông ABCD. Gọi H, K lần lượt là trung điểm của AB, AD. Trên đường thẳng vuông góc với (ABCD) tại H, lấy điểm S. Chứng minh rằng:

a) AC ⊥ (SHK) ;

b) CK ⊥ (SDH) .

Lời giải:

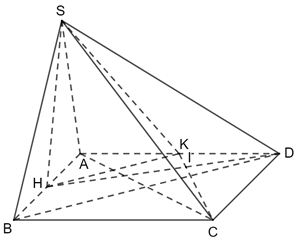
a) Xét tam giác ADB:

H là trung điểm AB

K là trung điểm AD

⇒ HK là đường trung bình của ΔADB.

$\left.\begin{array}{c}\Rightarrow \mathrm{HK} // \mathrm{BD}\\ \mathrm{AC} \perp \mathrm{BD}\end{array}\right\}\Rightarrow \text{AC}\perp \text{HK}$

Ta có:

$\left.\begin{array}{c}\mathrm{AC}\perp \mathrm{HK}\\ \mathrm{SH}\perp \left(\mathrm{ABCD}\right)\Rightarrow \mathrm{SH}\perp \mathrm{AC}\end{array}\right\}\Rightarrow \text{AC}\perp \left(\text{SHK}\right)$

b) Gọi $I=\mathrm{CK}\cap \mathrm{DH}$

Xét ΔAHD và ΔDKC:

AH = DK

$\widehat{\mathrm{HAD}}=\widehat{\mathrm{KDC}}$

AD = CD

⇒ ΔAHD = ΔDKC (c.g.c)

$\Rightarrow \widehat{\mathrm{HDA}}=\widehat{\mathrm{KCD}}$

Ta có: $\widehat{\mathrm{DKC}}+\widehat{\mathrm{KCD}}=90°$

$\Rightarrow \widehat{\mathrm{DKC}}+\widehat{\mathrm{HDA}}=90°$

$\Rightarrow \widehat{\mathrm{DKI}}=180°-\left(\widehat{\mathrm{KDC}}+\widehat{\mathrm{HDA}}\right)=90°$⇒ DH ⊥ CK

Mà SH ⊥ (ABCD) ⇒ SH ⊥ CK

Vậy CK ⊥ (SDH).

Bài 3 trang 64 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng $a\sqrt{2}$ , có các cạnh bên đều bằng 2a.

a) Tính góc giữa SC và AB .

b) Tính diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD) .

Lời giải:

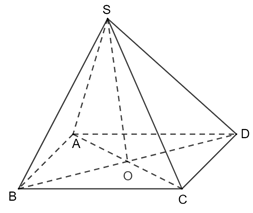
a) Ta có: AB // CD $\Rightarrow$ (SC, AB) = (SC, CD) = $\widehat{\mathrm{SCD}}$

Xét ΔSCD , áp dụng định lí cos, ta có :

$\cos \widehat{\mathrm{SCD}}=\frac{{\mathrm{SC}}^2+{\mathrm{CD}}^2-{\mathrm{SD}}^2}{2.\mathrm{SC}.\mathrm{SD}}=\frac{4a^2+2a^2-4a^2}{2.2a.2a}=\frac{1}{4}$

Do đó $\widehat{\mathrm{SCD}}\approx 75,5°$ .

b) Gọi $O=\mathrm{AC}\cap \mathrm{BD}$

Ta có:

ΔSAC cân tại S nên SO ⊥ AC (1)

ΔSBD cân tại S nên SO ⊥ BD (2)

Từ (1) và (2) suy ra SO ⊥ (ABCD)

Do đó O là hình chiếu vuông góc của S lên (ABCD).

Mà A, B ∈ (ABCD)

Vậy ΔOAB là hình chiếu vuông góc của ΔSAB lên (ABCD).

Ta có: AC = $\sqrt{\mathrm{AB}+\mathrm{BC}}=\sqrt{2a^2+2a^2}=2a$

Mà ABCD là hình vuông nên O là trung điểm của mỗi đường chéo.

⇒ $\mathrm{AO}$ = BO = $\frac{\mathrm{AC}}{2}=a$

⇒ $S_{\mathrm{OAB}}=\frac{1}{2}.\mathrm{AO}.\mathrm{BO}=\frac{1}{2}.a.a=\frac{a^2}{2}$ .

Vậy diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD) là $\frac{a^2}{2}$ .

Bài 4 trang 64 Toán 11 Tập 2: Cho hình chóp S.ABC có SA = SB = SC = a, $\widehat{\mathrm{ASB}}=90°,$ $\widehat{\mathrm{BSC}}=60°$ và $\widehat{\mathrm{ASC}}=120°$ . Gọi I là trung điểm cạnh AC . Chứng minh SI ⊥ (ABC) .

Lời giải:

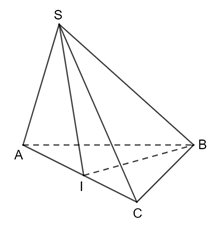
Tam giác SBC cân tại S (vì SB = SC = a ) có $\widehat{\mathrm{BSC}}={60}^{\text{o}}$

Suy ra ΔSBC đều nên BC = a

Áp dụng định lí Pythagore vào ΔSAB vuông tại S , ta có :

$\text{AB}=\sqrt{{\text{SA}}^2+{\text{SB}}^2}=\text{a}\sqrt{2}$

Lời giải:

Áp dụng định lí cos vào ΔSAC , ta có:

$\text{AC}=\sqrt{{\text{SA}}^2+\text{S}{C}^2-2.SA.SC.cos\widehat{ASC}}=\text{a}\sqrt{3}$

Ta có: AB² + BC² = AC² nên ΔABC vuông tại B (theo định lí Pythagore đảo) .

Lại có I là trung điểm AC nên $\mathrm{BI}=\frac{\mathrm{AC}}{2}=\frac{a\sqrt{3}}{2}$

ΔSAC cân tại S mà I là trung điểm của AC nên SI ⊥ AC (1)

$\Rightarrow \text{SI}=\sqrt{{\mathrm{SA}}^2-{\mathrm{AI}}^2}=\frac{a}{2}$

Ta có: SI² + IB² = SB² nên ΔSBI vuông tại I (theo định lí Pythagore đảo) .

Suy ra SI ⊥ IB (2)

Từ (1) và (2) suy ra SI ⊥ (ABC)

Bài 5 trang 64 Toán 11 Tập 2: Một cái lều có dạng hình lăng trụ ABC.A′B′C′ có cạnh bên AA′ vuông góc với đáy (Hình 24). Cho biết AB = AC = 2,4 m; BC = 2 m; AA′ = 3 m

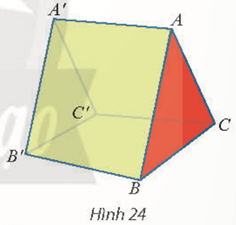
a) Tính góc giữa hai đường thẳng AA′ và BC; A ′B′ và AC.

b) Tính diện tích hình chiếu vuông góc của tam giác ABB′ trên mặt phẳng (BB ′CC′ ) .

Lời giải:

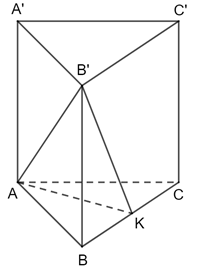
a) + Vì AA′ // BB ′ nên (AA′, BC) = (BB′, BC) = $\widehat{B\text{'}\mathrm{BC}}$

Ta có: AA ′ ⊥ (ABC), AA′ // BB ′ ⇒ BB ′ ⊥ (ABC) hay BB ′ ⊥ BC

⇒ $\widehat{B\text{'}\mathrm{BC}}=90°$

+ Vì A′B′ // AB nên (A ′B′, AC) = (AB, AC) = $\widehat{\mathrm{BAC}}$

ΔABC có:

$\cos \widehat{\mathrm{BAC}}=\frac{{\mathrm{AB}}^2+{\mathrm{AC}}^2-{\mathrm{BC}}^2}{2.\mathrm{AB}.\mathrm{AC}}=\frac{5.76+5,76-4}{2.2,4.2,4}=\frac{47}{72}$

⇒ $\widehat{\mathrm{BAC}}\approx 49,2°$

b) Kẻ AK ⊥ BC. Mà AA ′ ⊥ (ABC), AA ′ // BB′

⇒ BB ′ ⊥ (ABC)

⇒ BB ′ ⊥ AK (1)

Ta có: AK ⊥ BC; BC // B′C' ⇒ AK ⊥ B′C′ (2)

Từ (1) và (2) ⇒ AK ⊥ (BB′C′C)

⇒ K là hình chiếu vuông góc của A trên (BB ′ C ′ C)

Mà B, B ′ ∈ (BB ′ C ′ C)

Vậy ΔKBB ′ là hình chiếu vuông góc của ΔABB ′ lên (BB ′C′C ).

Ta có: ΔABC cân tại A có AK ⊥ BC K là trung điểm của BC

⇒ KB = KC = $\frac{\mathrm{BC}}{2}=1$

⇒ $S_{\mathrm{KBB}\text{'}}=\frac{1}{2}.\mathrm{BB}\text{'}.\mathrm{BK}=\frac{3}{2}$ .

Vậy diện tích hình chiếu vuông góc của tam giác ABB′ trên mặt phẳng (BB′CC′ ) là $\frac{3}{2}$ .