Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 33: Hai tam giác đồng dạng chi tiết sách Toán 8 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 33: Hai tam giác đồng dạng
Giải Toán 8 trang 78 Tập 2
Lời giải:
Quan sát thấy CD và AB song song với nhau.
Sử dụng định lí Thalès, ta nhận xét về hai tỉ lệ và .
Từ đó tìm ra tỉ số giữa các cạnh để tính chiều cao cột đèn.
1. Định nghĩa
Giải Toán 8 trang 79 Tập 2
Lời giải:
Ta thấy .
Lời giải:
Ta có ∆ABC ∽ ∆DEF với tỉ số đồng dạng .
Nhìn hình vẽ ta thấy tam giác GHK vuông tại G nên không thể đồng dạng với hai tam giác còn lại.
Định lí
Thử thách nhỏ trang 80 Toán 8 Tập 2: Cho ΔABC ∽ ΔMNP. Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì tam giác MNP cân tại đỉnh M.
b) Nếu tam giác ABC đều thì tam giác MNP đều.
c) Nếu AB ≥ AC ≥ BC thì MN ≥ MP ≥ NP.
Lời giải:
a) Tam giác ABC cân tại A nên . (1)
Vì ∆ABC ∽ ∆MNP nên ; . (2)
Từ (1) và (2) suy ra suy ra tam giác MNP cân tại M.
b) Vì tam giác ABC đều nên . (3)
Từ (1) và (3) suy ra nên tam giác MNP là tam giác đều.
c) Vì tam giác ABC có AB ≥ AC ≥ BC suy ra (quan hệ giữa góc và cạnh đối diện trong một tam giác). (4)
Từ (2) và (4) suy ra nên MN ≥ MP ≥ NP.
- Hãy viết các cặp góc bằng nhau của hai tam giác ABC và AMN, giải thích vì sao chúng bằng nhau.
- Kẻ đường thẳng đi qua N song song với AB và cắt BC tại P. Hãy chứng tỏ MN = BP và suy ra .
- Tam giác ABC và tam giác AMN có đồng dạng không? Nếu có hãy viết đúng kí hiệu đồng dạng.
Lời giải:
- Các cặp góc bằng nhau của hai tam giác ABC và AMN:
(do MN // BC và các cặp góc này ở vị trí đồng vị);
chung.
- Có MN // BP (vì MN // BC), MB // NP (vì AB // NP) nên MNPB là hình bình hành.
Suy ra MN = BP. Suy ra (Sử dụng định lí Thalès).
- Có ; chung và , suy ra ∆ABC ∽ ∆AMN.
Lời giải:
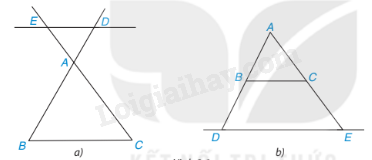
- Vì C ∊ OA, D ∊ OB và CD //AB nên ∆OCD ∽ ∆OAB.
- Vì E ∊ OB, F ∊ OA (thuộc phần kéo dài) và EF // AB nên ∆OEF ∽ ∆OBA.
- Vì F ∊ OC, E ∊ OD (thuộc phần kéo dài) và EF // CD nên ∆OEF ∽ ∆ODC.
Lời giải:
Có EB = 4 m = 400 cm, CD = 1 m = 100 cm.
Vì cọc gỗ và cột đèn đều thẳng đứng. Suy ra AB // DC. Do đó, ΔAEB ∽ ΔEDC.
Suy ra . Mà .
Vậy hai tam giác AEB và EDC đồng dạng với tỉ số .
Do đó, . Suy ra AB = 500 cm = 5 m.
Vậy chiều cao cột đèn là 5 m.
Bài tập
Bài 9.1 trang 82 Toán 8 Tập 2: Cho ∆ABC ∽ ∆MNP, khẳng định nào sau đây không đúng?
a) ∆MNP ∽ ∆ABC.
b) ∆BCA ∽ ∆NPM.
c) ∆CAB ∽ ∆PMN.
d) ∆ACB ∽ ∆MNP.
Lời giải:
Từ giả thiết ta thấy ∆ABC và ∆MNP đồng dạng với các cặp đỉnh tương ứng là A tương ứng M, B tương ứng N, C tương ứng P. Do đó các khẳng định a), b), c) đúng và khẳng định d) không đúng (do nếu viết theo d thì đỉnh C tương ứng với đỉnh N, đỉnh B tương ứng với đỉnh P).
Bài 9.2 trang 82 Toán 8 Tập 2: Những khẳng định nào sau đây là đúng?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác bất kì đồng dạng với nhau.
c) Hai tam giác đều bất kì đồng dạng với nhau.
c) Hai tam giác vuông bất kì đồng dạng với nhau.
d) Hai tam giác đồng dạng thì bằng nhau.
Lời giải:
+ Khẳng định a là khẳng định đúng vì các tam giác bằng nhau thì các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên tỉ số giữa các cạnh tương ứng bằng nhau nên theo định nghĩa hai tam giác đồng dạng thì hai tam giác bằng nhau thì đồng dạng với nhau.
+ Khẳng định c là khẳng định đúng vì tam giác đều thì có các góc bằng 60° và các cạnh bằng nhau nên ta suy ra các góc tương ứng của hai tam giác đều bất kì bằng nhau và tỉ số các cạnh tương ứng của hai tam giác đều bất kì bằng nhau.
+ Khẳng định b sai vì hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau từng đôi một và ba cặp cạnh tương ứng tỉ lệ.
+ Khẳng định d sai vì hai tam giác vuông mới chỉ thỏa mãn một điều kiện để xét đồng dạng, cần thêm tỉ lệ cạnh tương ứng hoặc 1 góc tương ứng bằng nhau.
+ Khẳng định e sai vì hai tam giác đồng dạng chỉ có kích thước tỉ lệ với nhau, còn hai tam giác bằng nhau là có các góc, các cạnh tương ứng bằng nhau.
Lời giải:
- Do N, P lần lượt là trung điểm của CA, AB.
Suy ra PN là đường trung bình của tam giác ABC nên NP // BC (P ∈ AB, N ∈ AC).
Suy ra ΔABC ∽ ΔAPN.
- Do M, P lần lượt là trung điểm của BC, AB.
Suy ra MP là đường trung bình của tam giác ABC nên MP // AC (P ∈ AB, M ∈ BC)
Suy ra ΔABC ∽ ΔPBM.
- Do M, N lần lượt là trung điểm của BC, AC.
Suy ra MN là đường trung bình của tam giác ABC nên MN // AB (N ∈ AC, M ∈ BC).
Suy ra ΔABC ∽ ΔNMC.
- Ta có (do ΔABC ∽ ΔPBM); (do PN // BC); (do cùng bằng góc C); .
Do đó, ΔAPN ∽ ΔPBM.
- Tương tự ta cũng có ΔNMC ∽ ΔPBM.
- Ta có ΔAPN = ΔMNP (g – c – g) vì ; (NP // BC và các cặp góc ở vị trí so le trong) và PN cạnh chung. Do đó ΔAPN ∽ ΔMNP.
Vậy ta có 5 tam giác APN, PBM, NMC, MNP, ABC đôi một đồng dạng với nhau.
Lời giải:
Vì tam giác ABC cân tại A nên . (1)
Tương tự, tam giác MNP cân tại M nên . (2)
Vì nên từ (1) và (2) suy ra .
Lấy B', C', lần lượt là trung điểm của AB, AC thì ta có B'C' // BC.
Do đó (các cặp góc đồng vị).
Hai tam giác AB'C' và MNP có:
(theo giả thiết);
(theo giả thiết);
\ (chứng minh trên).
Vậy ∆MNP = ∆AB'C' (g.c.g).
Mặt khác, ∆AB'C' ∽ ∆ABC (vì B'C' // BC).
Do đó, ∆MNP ∽ ∆ABC với tỉ số đồng dạng .
Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Bài 33: Hai tam giác đồng dạng
Bài 34: Ba trường hợp đồng dạng của hai tam giác
Bài 35: Định lí Pythagore và ứng dụng
Lý thuyết Hai tam giác đồng dạng
1. Định nghĩa
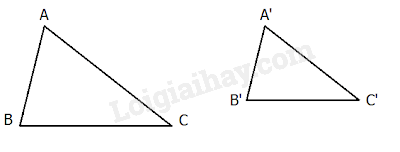
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
Kí hiệu: (viết theo thứ tự cặp đỉnh tương ứng).
Tỉ số là tỉ số đồng dạng của với .
Nhận xét:
- với tỉ số đồng dạng k thì với tỉ số đồng dạng . Ta nói hai tam giác A’B’C’ và ABC đồng dạng với nhau.
- Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng k = 1. Mọi tam giác đồng dạng với chính nó.
- với tỉ số đồng dạng k và với tỉ số đồng dạng m thì với tỉ số đồng dạng k.m.
2. Định lí
Nếu một đường thẳng cắt hai cạnh của một tam giác là song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
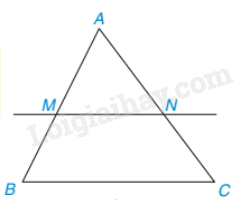
Chú ý. Định lí trên vẫn đúng nếu thay bằng đường thẳng cắt phần kéo dài của hai cạnh tam giác.