Giải SGK Toán 8 Bài 34 (Kết nối tri thức): Ba trường hợp đồng dạng của hai tam giác

Van Anh Ngày: 23-09-2024 Lớp 8

5.8 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác chi tiết sách Toán 8 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác

1. Trường hợp đồng dạng thứ nhất của tam giác

Giải Toán 8 trang 83 Tập 2

Mở đầu trang 83 Toán 8 Tập 2: Trong môn Bóng đá, độ khó của mỗi pha ghi bàn còn được tính bởi góc sút vào cầu môn là rộng hay hẹp. Nếu biết độ rộng của khung thành là 7,32 m, trái bóng cách hai cột gôn lần lượt là 10,98 m và 14,64 m thì em có cách nào để đo được góc sút ở vị trí này bởi các dụng cụ học tập không?

Mở đầu trang 83 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Lời giải:

Vì trong hình vẽ mặt sân được vẽ nghiêng nên nếu đo trực tiếp trong sách giáo khoa sẽ không đúng bằng góc thực tế.

Vẽ một tam giác bằng dụng cụ học tập trên giấy có một góc đúng bằng góc sút. Từ đó sử dụng dụng cụ học tập là thước đo góc để đo góc sút.

HĐ1 trang 83 Toán 8 Tập 2: Cho hai tam giác ABC và A'B'C' có $\frac{A' B'}{A B} = \frac{A' C'}{A C} = \frac{B' C'}{B C}$ .

a) Nếu A′B' = AB thì hai tam giác có đồng dạng với nhau không? Vì sao?

b) Nếu A′B' < AB như Hình 9.11. Trên đoạn thẳng AB lấy điểm M sao cho AM = A′B′. Kẻ đường thẳng qua M song song với BC và cắt AC tại N.

- Hãy giải thích vì sao ΔAMN ∽ ΔABC.

- Hãy chứng tỏ rằng AN = A′C′, MN = B′C′ để suy ra ΔAMN = ΔA'B'C' (c.c.c).

- Hai tam giác A'B'C' và ABC có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.

c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Vì sao?

HĐ1 trang 83 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Lời giải:

a) Nếu A′B′ = AB thì từ $\frac{A' B'}{A B} = \frac{A' C'}{A C} = \frac{B' C'}{B C}$ , suy ra A′C′ = AC và B′C′ = BC.

Do đó ΔABC = ΔA'B'C' (c.c.c). Vậy ΔABC ∽ ΔA'B'C'.

b) Ta có MN // BC ( M ∈ AB, N ∈ AC). Suy ra ΔAMN ∽ ΔABC.

Suy ra $\frac{A M}{A B} = \frac{A N}{A C} = \frac{M N}{B C}$ .

Mà $\frac{A' B'}{A B} = \frac{A' C'}{A C} = \frac{B' C'}{B C}$ nên $\frac{A' B'}{A M} = \frac{A' C'}{A N} = \frac{B' C'}{M N}$ .

Có AM = A'B', suy ra A'C' = AN và B'C' = MN nên ∆AMN = ∆A'B'C' (c.c.c).

Suy ra ∆AMN ∽ ∆A'B'C', mà ∆AMN ∽ ∆ABC nên ∆ABC ∽ ∆A'B'C'.

c) Nếu A'B' > AB, bằng cách đổi vai trò cho ∆ABC và ∆A'B'C' cho nhau thì theo câu b), ta có ∆ABC ∽ ∆A'B'C'.

Giải Toán 8 trang 84 Tập 2

Câu hỏi trang 84 Toán 8 Tập 2: Những cặp tam giác nào dưới đây (H.9.13) là đồng dạng? (các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.

Câu hỏi trang 84 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Lời giải:

Ta có ∆ABC ∽ ∆HGK (c.c.c) vì $\frac{A B}{H G} = \frac{B C}{G K} = \frac{A C}{H K} = \frac{1}{2}$ .

Ta có ∆DEF ∽ ∆MNP (c.c.c) vì $\frac{D E}{M N} = \frac{E F}{N P} = \frac{D F}{M P} = \frac{1}{2}$ .

Giải Toán 8 trang 85 Tập 2

Luyện tập 1 trang 85 Toán 8 Tập 2: Cho tam giác ABC có chu vi bằng 18 cm và tam giác DEF có chu vi bằng 27 cm. Biết rằng AB = 4 cm, BC = 6 cm, DE = 6 cm, FD = 12 cm. Chứng minh ΔABC ∽ ΔDEF.

Lời giải:

Vì chu vi tam giác ABC bằng 18 cm.

Suy ra AB + AC + BC = 18. Suy ra 4 + AC + 6 = 18 nên AC = 8 (cm).

Vì chu vi tam giác DEF bằng 27 cm.

Suy ra DE + EF + DF = 27. Suy ra 6 + EF + 12 = 27 nên EF = 9 (cm)

Ta thấy: $\frac{A B}{D E} = \frac{A C}{D F} = \frac{B C}{E F} = \frac{4}{6} = \frac{8}{12} = \frac{6}{9} = \frac{2}{3}$ .

Suy ra ∆ABC ∽ ∆DEF (c.c.c).

Vận dụng trang 85 Toán 8 Tập 2: Trở lại tình huống mở đầu. Em hãy vẽ một tam giác có ba cạnh tỉ lệ với ba cạnh của tam giác tạo bởi ba đỉnh là trái bóng và hai chân cột gôn. Từ đó tính góc sút bằng góc tương ứng của tam giác vừa vẽ được.

Vuông: Tớ sẽ tính tỉ lệ (7,32 : 10,98 : 14,64) bằng (1 : 1,5 : 2).

Tròn: Tớ sẽ tính tỉ lệ (7,32 : 10,98 : 14,64) bằng (2 : 3 : 4).

Lời giải:

Có thể vẽ tam giác ABC có các cạnh lần lượt bằng 2 cm; 3 cm; 4 cm sau đó xét các tỉ lệ ta thấy $\frac{7,32}{2} = \frac{10,98}{3} = \frac{14,64}{4} = 3,66$ nên tam giác ABC đồng dạng với tam giác tạo bởi ba đỉnh là trái bóng và hai chân cột gôn.

Lấy thước đo góc để đo các góc của tam giác từ đó tính được góc sút.

Ta đo được góc sút bằng khoảng 29°.

2. Trường hợp đồng dạng thứ hai của tam giác

HĐ2 trang 85 Toán 8 Tập 2: Cho hai tam giác ABC và A'B'C' có độ dài các cạnh (theo đơn vị cm) như Hình 9.15. Biết rằng $\hat{A} = \hat{A'} = 60 °$ .

HĐ2 trang 85 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

- So sánh các tỉ số $\frac{A' B'}{A B}, \frac{A' C'}{A C}$ .

- Dùng thước có vạch chia đo độ dài BC, B'C' và tính tỉ số $\frac{B' C'}{B C}$ .

- Theo em, tam giác A'B'C' có đồng dạng với tam giác ABC không? Nếu có thì tỉ số đồng dạng là bao nhiêu?

Lời giải:

- Ta có: $\frac{A' B'}{A B} = \frac{A' C'}{A C} = \frac{3}{2}$ .

- Đo được BC ≈ 2,6 cm; B'C' ≈ 3,9 cm.

Tỉ số $\frac{B' C'}{B C} = \frac{3}{2}$ . Do đó $\frac{A' B'}{A B} = \frac{A' C'}{A C} = \frac{B' C'}{B C}$ .

- Vậy ∆A'B'C' ∽ ∆ABC (c.c.c) với tỉ số đồng dạng là $\frac{3}{2}$ .

Giải Toán 8 trang 86 Tập 2

Câu hỏi trang 86 Toán 8 Tập 2: Những cặp tam giác nào trong Hình 9.17 là đồng dạng? (Các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.

Câu hỏi trang 86 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Lời giải:

Ta có ∆ACB ∽ ∆MPN vì $\hat{A} = \hat{M} = 70 °$ và $\frac{A C}{M P} = \frac{A B}{M N} = \frac{1}{2}$ .

Giải Toán 8 trang 87 Tập 2

Luyện tập 2 trang 87 Toán 8 Tập 2: Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho $\frac{M C}{M B} = \frac{M' C'}{M' B'}$ . Chứng minh rằng ΔA'B'M' ∽ ΔABM.

Lời giải:

Luyện tập 2 trang 87 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Có $\frac{M C}{M B} = \frac{M' C'}{M' B'}$ . Suy ra $\frac{M B - B C}{M B} = \frac{M' B' - B' C'}{M' B'}$

Suy ra $1 - \frac{B C}{M B} = 1 - \frac{B' C'}{M' B'}$ . Do đó, $\frac{B C}{M B} = \frac{B' C'}{M' B'}$ , suy ra $\frac{B' C'}{B C} = \frac{M' B'}{M B}$ . (1)

Vì ΔA′B′C′ ∽ ΔABC. Suy ra $\hat{B} = \hat{B'}$ và $\frac{A' B'}{A B} = \frac{B' C'}{B C}$ . (2)

Từ (1) và (2) suy ra $\frac{M' B'}{M B} = \frac{A' B'}{A B}$ .

Xét tam giác ABM và tam giác A'B'M' có:

$\frac{M' B'}{M B} = \frac{A' B'}{A B}$ và $\hat{B} = \hat{B'}$ (chứng minh trên).

Do đó ΔABM ∽ ΔA′B′M′ (c.g.c).

Tranh luận trang 87 Toán 8 Tập 2: Bạn Lan nhận xét rằng nếu tam giác ABC và tam giác A'B'C' có $\frac{A' B'}{A B} = \frac{A' C'}{A C}$ và $\hat{B} = \hat{B'}$ thì chúng đồng dạng. Theo em bạn Lan nhận xét đúng không vì sao?

Gợi ý: Khi góc ACB tù, lấy điểm M trên tia BC sao cho tam giác AMC cân (H.9.19) rồi xét xem trong hai tam giác ABC và ABM, tam giác nào đồng dạng với tam giác A'B'C'.

Tranh luận trang 87 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Lời giải:

Bạn Lan nhận xét không đúng.

Ví dụ lấy ∆ABM ∽ ∆A'B'C' với $\hat{C'} = \hat{M} < 90 °$ và lấy C trên đoạn MB sao cho ∆AMC cân tại A như H.9.19 thì ∆ABC và ∆A'B'C' không đồng dạng.

3. Trường hợp đồng dạng thứ ba của tam giác

Giải Toán 8 trang 88 Tập 2

HĐ3 trang 88 Toán 8 Tập 2: Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB = 10 m, $\hat{A B C} = 70 °; \hat{B A C} = 80 °$ và vẽ một tam giác A'B'C' trên giấy với A′B′ = 2 cm, $\hat{A' B' C'} = 70 °; \hat{B' A' C'} = 80 °$ .(H.9.20b).

HĐ3 trang 88 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Em hãy dự đoán xem tam giác A'B'C' có đồng dạng với tam giác ABC không. Nếu có thì tỉ số đồng dạng là bao nhiêu?

Lời giải:

Dự đoán: Hai tam giác có hình dạng rất giống nhau chỉ khác về kích thước nên chúng có khả năng đồng dạng với nhau. Khi đó tỉ số đồng dạng bằng $\frac{A' B'}{A B} = \frac{2}{1000} = \frac{1}{500}$ .

(AB = 10 m = 1 000 cm, A'B' = 2 cm)

HĐ4 trang 88 Toán 8 Tập 2: Nếu ΔA'B'C' ∽ ΔABC và anh Pi đo được A′C′ = 3,76 cm thì khoảng cách từ bạn Tròn đến chân cột cờ là bao nhiêu mét?

Lời giải:

Nếu ΔA'B'C'∽ ΔABC thì $\frac{A' C'}{A C} = \frac{A' B'}{A B} = \frac{B' C'}{B C}$ .

Mà A'C' = 3,76 cm và $\frac{A' C'}{A C} = \frac{A' B'}{A B}$ , suy ra $A C = \frac{A' C'}{A' B'} . A B = \frac{3,76 : 100}{2 : 100} \cdot 10 = 18,8 (m)$

Giải Toán 8 trang 89 Tập 2

Câu hỏi trang 89 Toán 8 Tập 2: Những cặp tam giác nào trong Hình 9.22 là đồng dạng? Viết đúng kí hiệu đồng dạng.

Câu hỏi trang 89 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Lời giải:

Xét tam giác MPN có:

$\hat{P} = 180 ° - \hat{M} - \hat{N} = 180 ° - 60 ° - 70 ° = 50 °$ .

Các cặp tam giác đồng dạng trong Hình 9.22 là:

+) ΔACB ∽ ΔDFE (g.g) vì $\hat{A} = \hat{D} = 60 °; \hat{B} = \hat{E} = 50 °$ .

+) ΔACB ∽ ΔMNP (g.g) vì $\hat{A} = \hat{M} = 60 °; \hat{B} = \hat{P} = 50 °$ .

+) ΔDEF ∽ ΔMPN (g.g) vì $\hat{D} = \hat{M} = 60 °; \hat{E} = \hat{P} = 50 °$ .

Luyện tập 3 trang 89 Toán 8 Tập 2: Cho các điểm A, B, C, D như Hình 9.24. Biết rằng $\hat{A B C} = \hat{A D B}$ . Hãy chứng minh ΔABC ∽ ΔADB và AB² = AD . AC.

Luyện tập 3 trang 89 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Lời giải:

Xét tam giác ABC và tam giác ADB có:

$\hat{A B C} = \hat{A D B}$ và $\hat{A}$ chung

Do đó ΔABC ∽ ΔADB (g.g).

Suy ra $\frac{A B}{A D} = \frac{A C}{A B}$ , do đó AB . AB = AD . AC hay AB² = AD . AC.

Giải Toán 8 trang 90 Tập 2

Thử thách nhỏ trang 90 Toán 8 Tập 2: 1. Biết rằng ba đường phân giác của tam giác ABC đồng quy tại I, ba đường phân giác của tam giác A'B'C' đồng quy tại I'. Hãy chứng tỏ rằng nếu $\hat{A' I' B'} = \hat{A I B}$ và $\hat{A' I' C'} = \hat{A I C}$ thì ∆A'B'C' ∽ ∆ABC.

2. Với hai tam giác ABC và A'B'C' trong phần Tranh luận, nếu thêm giải thiết các góc C và C' nhọn thì hai tam giác đó có đồng dạng không?

Lời giải:

Thử thách nhỏ trang 90 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Do tổng các góc trong một tam giác bằng 180^○ nên:

$\frac{\hat{A'} + \hat{B'}}{2} = 180 ° - \hat{A' I' B'} = 180 ° - \hat{A I B} = \frac{\hat{A} + \hat{B}}{2}$ .

Suy ra $\hat{A'} + \hat{B'} = \hat{A} + \hat{B}$ . Do đó $\hat{C'} = 180 ° - \hat{A'} - \hat{B'} = 180 ° - \hat{A} - \hat{B} = \hat{C}$ .

Tương tự ta có $\hat{B} = \hat{B'}$ . Vậy tam giác ABC và A'B'C' có: $\hat{B} = \hat{B'}$ ; $\hat{C} = \hat{C'}$ .

Do đó ∆ABC ∽ ∆A'B'C' (g.g).

2. Nếu góc C và góc C' đều nhọn, lấy điểm M trên tia BC sao cho ∆ABM ∽ ∆A'B'C'.

Giả sử điểm C không trùng với M.

Khi đó ∆ABM ∽ ∆A'B'C' nên $\frac{A' C'}{A M} = \frac{A' B'}{A B} = \frac{B' C'}{B M}$ .

Mà $\frac{A' B'}{A B} = \frac{A' C'}{A C}$ (gt) nên $\frac{A' C'}{A M} = \frac{A' C'}{A C}$ , suy ra AC = AM hay ∆AMC cân tại A.

+) Nếu M nằm giữa B và C thì

$\hat{A M B} = 180 ° - \hat{A M C} = 180 ° - \hat{A C M} > 90 ° > \hat{C'}$ (Vô lí).

+) Nếu C nằm giữa B và M (như Hình 9.19). Khi đó

$\hat{A C B} = 180 ° - \hat{A C M} = 180 ° - \hat{A M B} = 180 ° - \hat{C'} > 90 °$ (Vô lí).

Vậy điểm C phải trùng với M và ∆ABC ∽ ∆A'B'C'.

Bài tập

Bài 9.5 trang 90 Toán 8 Tập 2: Giả thiết nào dưới đây chứng tỏ rằng hai tam giác đồng dạng?

a) Ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.

b) Hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và có một cặp góc bằng nhau.

c) Hai góc của tam giác này bằng hai góc của tam giác kia.

d) Hai cạnh của tam giác này bằng hai cạnh của tam giác kia.

Lời giải:

Giả thiết a) suy ra hai tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh.

Giả thiết c) suy ra hai tam giác đồng dạng theo trường hợp góc – góc.

Các giả thiết b) và d) không suy ra hai tam giác đồng dạng.

Bài 9.6 trang 90 Toán 8 Tập 2: Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4 cm, 8 cm và 10 cm. Tam giác thứ hai có chu vi là 33 cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?

a) 6 cm, 12 cm, 15 cm. b) 8 cm, 16 cm, 20 cm.

c) 6 cm, 9 cm, 18 cm. d) 8 cm, 10 cm, 15 cm.

Lời giải:

Vì 6 + 12 + 15 = 33 (cm) và $\frac{4}{6} = \frac{8}{12} = \frac{10}{15}$ nên bộ ba trong câu a) là độ dài ba cạnh của tam giác thỏa mãn yêu cầu. Các bộ ba còn lại hoặc không có tổng bằng 33 cm hoặc không có tỉ lệ tương ứng với (4 : 8 : 10) nên không thể là độ dài ba cạnh của tam giác thỏa mãn yêu cầu.

Bài 9.7 trang 90 Toán 8 Tập 2: Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA′B′C′ ∽ ΔABC.

Chứng minh rằng $\frac{A' M'}{A M} = \frac{B' N'}{B N} = \frac{C' P'}{C P}$

Lời giải:

Bài 9.7 trang 90 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Vì ΔA′B′C′ ∽ ΔABC nên: $\frac{A' B'}{A B} = \frac{B' C'}{B C} = \frac{A' C'}{A C}$ ; (1)

và $\hat{A' B' C'} = \hat{A B C}; \hat{B' C' A'} = \hat{B C A}; \hat{C' A' B'} = \hat{C A B}$ . (2)

Hai tam giác A'B'M' và ABM có:

$\frac{B' M'}{B M} = \frac{\frac{B' C'}{2}}{\frac{B C}{2}} = \frac{B' C'}{B C} = \frac{B' A'}{B A}$ (theo (1));

$\hat{A' B' M'} = \hat{A' B' C'} = \hat{A B C} = \hat{A B M}$ (theo (2)).

Do đó ΔA′M′B′ ∽ ΔAMB (c.g.c). Suy ra $\frac{A' M'}{A M} = \frac{A' B'}{A B}$ (3).

Tương tự ΔA′C′P′ ∽ ΔACP và $\frac{C' P'}{C P} = \frac{A' C'}{A C}$ (4).

ΔA′B′N′ ∽ ΔABN và $\frac{B' N'}{B N} = \frac{A' B'}{A B}$ (5).

Từ (1), (3), (4) và (5) suy ra $\frac{A' M'}{A M} = \frac{B' N'}{B N} = \frac{C' P'}{C P}$ .

Bài 9.8 trang 90 Toán 8 Tập 2: Cho tam giác ABC có AB = 12 cm, AC = 15 cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM = 10 cm, AN = 8 cm. Chứng minh rằng ΔABC ∽ ΔANM

Lời giải:

Bài 9.8 trang 90 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Có AB = 12 cm , AN = 8 cm. Suy ra $\frac{A N}{A B} = \frac{8}{12} = \frac{2}{3}$ .

AC = 15 cm, AM = 10 cm. Suy ra $\frac{A M}{A C} = \frac{10}{15} = \frac{2}{3}$ .

Suy ra $\frac{A N}{A B} = \frac{A M}{A C}$ .

Xét hai tam giác ABC và tam giác ANM có:

$\frac{A N}{A B} = \frac{A M}{A C}$ , $\hat{A}$ chung.

Do đó ΔABC ∽ ΔANM (c.g.c).

Bài 9.9 trang 90 Toán 8 Tập 2: Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho $\hat{A B N} = \hat{A C M}$ .

a) Chứng minh rằng ΔABN ∽ ΔACM.

b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB . IN = IC . IM.

Lời giải:

Bài 9.9 trang 90 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

a) Xét tam giác ABN và tam giác ACM:

$\hat{A}$ chung, $\hat{A B N} = \hat{A C M}$ (giả thiết)

Suy ra ΔABN ∽ ΔACM (g.g).

b) Vì ΔABN ∽ ΔACM (chứng minh trên) nên $\hat{A N B} = \hat{A M C}$ .

Lại có: $\hat{A N B} + \hat{C N B} = 180 °; \hat{A M C} + \hat{B M C} = 180 °$ (kề bù), suy ra $\hat{C N B} = \hat{B M C}$ .

Xét tam giác IBM và tam giác ICN có:

$\hat{C N B} = \hat{B M C}$ (cmt) và $\hat{I B M} = \hat{I C N}$ (do $\hat{A B N} = \hat{A C M}$ )

Suy ra ΔIBM ∽ ΔICN (g.g).

Suy ra $\frac{I B}{I C} = \frac{I M}{I N}$ . Suy ra IB . IN = IC . IM.

Bài 9.10 trang 90 Toán 8 Tập 2: Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3 m và 2 m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25). Hãy tính độ cao h của điểm đó so với mặt đất.

Bài 9.10 trang 90 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Lời giải:

Bài 9.10 trang 90 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Kí hiệu các điểm như hình vẽ trên.

Ta có: AB, EF, CD đôi một song song vì cùng vuông góc với BC (do dựng thẳng đứng).

Do đó ΔCEF ∽ ΔCAB và ΔBEF ∽ ΔBDC.

Suy ra $\frac{E F}{A B} = \frac{C F}{C B}$ và $\frac{E F}{C D} = \frac{B F}{B C}$ .

Do đó: $\frac{E F}{C D} + \frac{E F}{A B} =$ $\frac{B F}{B C} + \frac{C F}{C B} = \frac{B F + C F}{B C} = \frac{B C}{B C}$ .

Suy ra $\frac{E F (A B + C D)}{C D \cdot B A} = 1$ .

Vậy $h = E F = \frac{C D \cdot A B}{A B + C D} = \frac{2 \cdot 3}{3 + 2} = \frac{6}{5} = 1,2$ (m).

Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Bài 33: Hai tam giác đồng dạng

Bài 34: Ba trường hợp đồng dạng của hai tam giác

Luyện tập chung (trang 91)

Bài 35: Định lí Pythagore và ứng dụng

Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Lý thuyết Ba trường hợp đồng dạng của hai tam giác

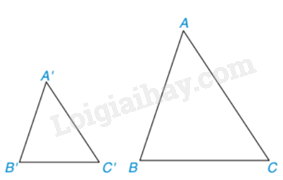
1. Trường hợp đồng dạng thứ nhất của tam giác

Trường hợp đồng dạng cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.

${\begin{cases} Δ A B C, Δ A^{'} B^{'} C^{'}; \\ \frac{A^{'} B^{'}}{A B} = \frac{B^{'} C^{'}}{B C} = \frac{A^{'} C^{'}}{A C} \end{cases} \Rightarrow Δ A^{'} B^{'} C^{'} ∽ Δ A B C$

Lý thuyết Ba trường hợp đồng dạng của hai tam giác (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 1)

2. Trường hợp đồng dạng thứ hai của tam giác

Trường hợp đồng dạng cạnh – góc – cạnh:

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.

${\begin{cases} Δ A B C, Δ A^{'} B^{'} C^{'}; \\ \frac{A^{'} B^{'}}{A B} = \frac{A^{'} C^{'}}{A C}, \hat{A^{'}} = \hat{A} \end{cases} \Rightarrow Δ A^{'} B^{'} C^{'} ∽ Δ A B C$

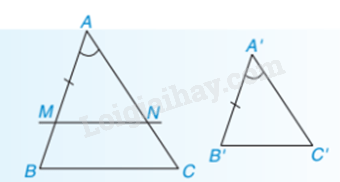
Lý thuyết Ba trường hợp đồng dạng của hai tam giác (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 2)

Nhận xét: Nếu $Δ A^{'} B^{'} C^{'} ∽ Δ A B C$ theo tỉ số k và AM, A’M’ lần lượt là các đường trung tuyến của $Δ A B C$ và $Δ A^{'} B^{'} C^{'}$ thì $\frac{A^{'} M^{'}}{A M} = k$

3. Trường hợp đồng dạng thứ ba của tam giác

Trường hợp đồng dạng góc – góc:

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

${\begin{cases} Δ A B C, Δ A^{'} B^{'} C^{'}; \\ \hat{A^{'}} = \hat{A}, \hat{B^{'}} = \hat{B} \end{cases} \Rightarrow Δ A^{'} B^{'} C^{'} ∽ Δ A B C$

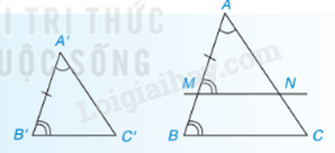
Lý thuyết Ba trường hợp đồng dạng của hai tam giác (Kết nối tri thức 2023) hay, chi tiết | Lý thuyết Toán lớp 8 (ảnh 3)

Nhận xét: $Δ A^{'} B^{'} C^{'} ∽ Δ A B C$ theo tỉ số k và AM, A’M’ lần lượt là các đường phân giác của $Δ A B C$ và $Δ A^{'} B^{'} C^{'}$ thì $\frac{A^{'} M^{'}}{A M} = k$