Tailieumoi.vn xin giới thiệu Bài tập Chứng minh hai tam giác đồng dạng lớp 8 được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Hình đồng dạng. Mời các bạn đón xem:
Bài tập Chứng minh hai tam giác đồng dạng lớp 8
A. Bài tập Chứng minh Hai tam giác đồng dạng
Bài 1: Cho tam giác ABC và các đường cao BH, CK. Chứng minh Δ ABH ∼ Δ ACK.
Lời giải:
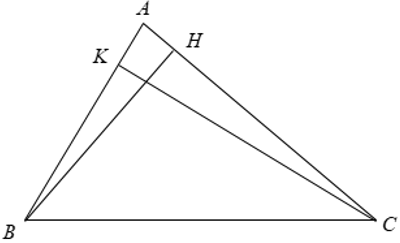
Xét Δ ABH và Δ ACK có 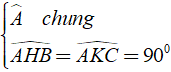
⇒ Δ ABH ∼ Δ ACK ( g - g )
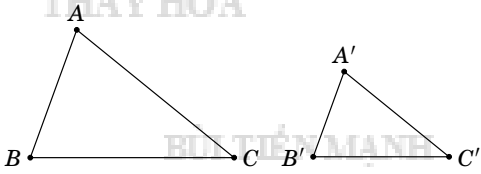
Bài 2: Cho Δ ABC,Δ A'B'C' có độ dài các cạnh như hình vẽ. Chứng minh Δ ABC ∼ Δ A'B'C'
Lời giải:
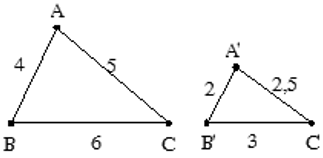
Xét Δ ABC,Δ A'B'C' có A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.
⇒ Δ ABC ∼ Δ A'B'C' ( c - c - c )
Bài 3: Cho góc 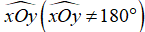 . Trên Ox lấy hai điểm A,B sao cho OA = 3cm, OB = 8cm. Trên Oy lấy hai điểm C,D sao cho OC = 4cm, OD = 6cm.
. Trên Ox lấy hai điểm A,B sao cho OA = 3cm, OB = 8cm. Trên Oy lấy hai điểm C,D sao cho OC = 4cm, OD = 6cm.
a. Chứng minh rằng hai tam giác ΔOAD và ΔOCB đồng dạng.
b. Gọi I là giao điểm của AD và BC. Chứng minh rằng hai tam giác ΔIAB và ΔICD có các góc bằng nhau từng đôi một.
Lời giải:
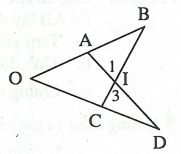
a. Với hai tam giác ΔOAD và ΔOCB, ta có :
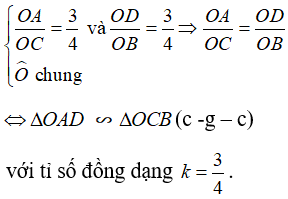
b. Vì ΔOAD và ΔOCB(cmt) 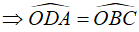 (hai góc tương ứng)
(hai góc tương ứng)
Với hai tam giác ΔIAB và ΔICD, ta có :
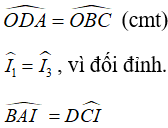
(dựa trên tính chất tổng ba góc trong tam giác bằng 1800).
Vậy, hai tam giác ΔIAB và ΔICD có các góc bằng nhau từng đôi một.
B. Lý thuyết Hai tam giác đồng dạng
1. Tam giác đồng dạng
a) Định nghĩa
Hai tam giác được gọi là đồng dạng với nhau nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Tam giác ABC gọi là đồng dạng với tam giác A'B'C' nếu
Kí hiệu: Δ ABC ∼ Δ A'B'C'
Tỉ số cách cạnh tương ứng A'B'/AB = A'C'/AC = B'C'/BC = k được gọi là tỉ số đồng dạng
b) Tính chất
Hai tam giác A'B'C' và ABC đồng dạng có một số tính chất:
+ Δ ABC ∼ Δ A'B'C'
+ Nếu Δ ABC ∼ Δ A'B'C' thì Δ A'B'C' ∼ Δ ABC.
+ Nếu Δ A'B'C' ∼ Δ A''B''C'' và Δ A''B''C'' ∼ Δ ABC thì Δ ABC ∼ Δ A'B'C'
2. Định lý
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
Tổng quát: Δ ABC,DE//BC ( D ∈ AB; E ∈ AC ).
Ta có: Δ ADE ∼ Δ ABC
Chú ý: Định lí cũng đúng cho trường hợp đường thẳng d cắt phần kéo dài của hai tam giác song song với cạnh còn lại.
C. Các dạng bài tập Tam giác đồng dạng
1. Chứng minh hai tam giác đồng dạng – trường hợp đồng dạng thứ nhất (C-C-C)
Phương pháp giải
 Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
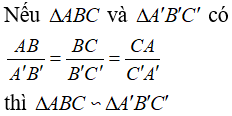
+) Xếp các cạnh của hai tam giác theo cùng một thứ tự (chẳng hạn từ nhỏ tới lớn).
+) Lập ba tỉ số, nếu chúng bằng nhau thì hai tam giác đồng dạng.
Ví dụ: Cho 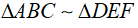 theo tỉ số
theo tỉ số 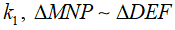 theo tỉ số k2. Chứng minh
theo tỉ số k2. Chứng minh 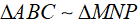 theo tỉ số
theo tỉ số 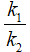 ?
?
Lời giải:
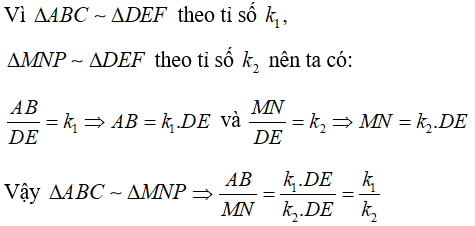
2. Chứng minh hai tam giác đồng dạng – trường hợp đồng dạng thứ hai (C–G–C)
Phương pháp giải
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
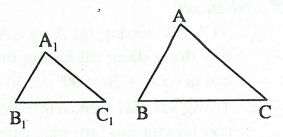 Như vậy, nếu hai tam giác ΔABC và ΔA1B1C1 thỏa mãn:
Như vậy, nếu hai tam giác ΔABC và ΔA1B1C1 thỏa mãn:
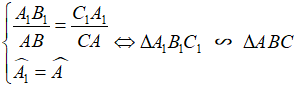
Và khi đó, ta có ngay :
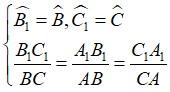
+) Xét hai tam giác, chọn ra hai góc bằng nhau, xét tỉ số hai cạnh tạo nên mỗi góc đó. Nếu hai tỉ số bằng nhau thì hai tam giác đồng dạng.
Ví dụ: Cho ΔABC có AB = 4cm, AC = 5cm, BC = 6cm. Trên tia đối của tia AB lấy điểm D sao cho AD = 5cm.
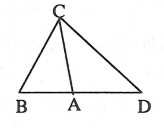 a. Tam giác ABC đồng dạng với tam giác nào ?
a. Tam giác ABC đồng dạng với tam giác nào ?
b. Tính độ dài CD.
c. Chứng minh rằng 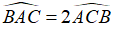 .
.
Lời giải:
a. Ta có :
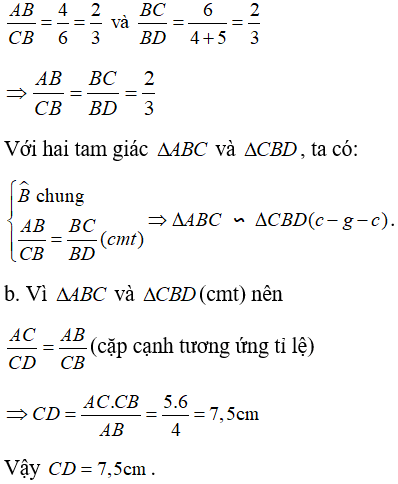

3. Chứng minh hai tam giác đồng dạng - trường hợp đồng dạng thứ ba (G-G)
Phương pháp giải
Định lí: Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đồng dạng.
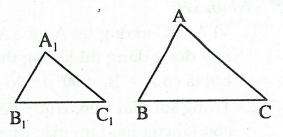 Như vậy, nếu hai tam giác ΔABC và ΔA1B1C1 thỏa mãn:
Như vậy, nếu hai tam giác ΔABC và ΔA1B1C1 thỏa mãn:
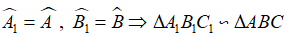
Và khi đó ta có:
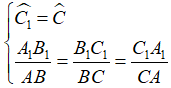
Ví dụ: Cho ΔABC vuông tại A, đường cao AD, đường phân giác BE. Giả sử AD cắt BE tại F. Chứng minh rằng 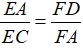 .
.
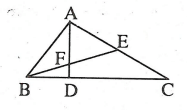
Lời giải:
Trong ΔABD có BF là phân giác suy ra:
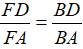 (tính chất) (1)
(tính chất) (1)
Với hai tam giác ΔABD và ΔABC, ta có nhận xét:
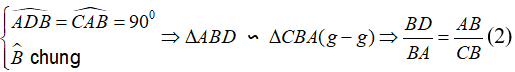
(cặp cạnh tương ứng)
Trong ΔABC có BE là phân giác suy ra:
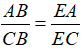 (3)
(3)
Từ (1), (2), (3) suy ra 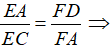 đpcm.
đpcm.