Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Hai tam giác đồng dạng được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Hai tam giác đồng dạng. Mời các bạn đón xem:
Bài tập Toán 8 Hai tam giác đồng dạng
A. Bài tập Hai tam giác đồng dạng
Bài 1: Hãy chọn câu đúng.
A. Hai tam giác bằng nhau thì đồng dạng.
B. Hai tam giác đồng dạng thì bằng nhau.
C. Hai tam giác bằng nhau thì không đồng dạng.
D. Hai tam giác vuông luôn đồng dạng với nhau.
Hướng dẫn giải:
Đáp án : A
+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên câu A đúng, câu C sai.
+ Hai tam giác đồng dạng thì chưa chắc bằng nhau nó chỉ bằng nhau khi tỉ số đồng dạng bằng 1 nên câu B sai.
+ Hai tam giác vuông chưa chắc đồng dạng (chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau) nên câu D sai.
Bài 2: Nếu theo tỉ số thì theo tỉ số
A. .
B. .
C. .
D. .
Hướng dẫn giải:
Đáp án : B
Vì theo tỉ số đồng dạng là theo tỉ số đồng dạng là
Bài 3: Cho . Biết . Hãy chọn đáp án đúng:
Hướng dẫn giải:
Đáp án : B
Vì (hai cạnh tương ứng)
Bài 4: Cho theo tỉ số và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.
Hướng dẫn giải:
Đáp án : D
Vì theo tỉ số
Bài 5: Cho tam giác ABC , lấy M trên cạnh BC sao cho Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là
Hướng dẫn giải:
Đáp án : A
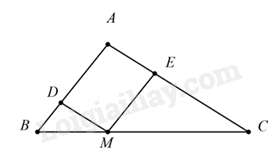
Vì MD // AC
Vì ME // AB
Mà chu vi tam giác MEC bằng 24 cm
Chu vi tam giác DBM bằng 24 : 2 = 12 (cm).
Bài 6: Cho theo tỉ số , theo tỉ số . Hỏi theo tỉ số nào ?
Vì theo tỉ số
Vì theo tỉ số
Bài 7: Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.

Vì AB // DE (định lí)
(các cạnh tương ứng)
Bài 8: Cho theo tỉ số và theo tỉ số 1 :3. Vậy theo tỉ số k bằng
Vì theo tỉ số
Vì theo tỉ số
Vậy theo tỉ số .
Bài 9: Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
, tỉ số đồng dạng
, tỉ số đồng dạng
, tỉ số đồng dạng
Chọn câu đúng:

Xét có (gt) theo tỉ số đồng dạng
Vì ABCD là hình bình hành nên
+
+ (so le trong)
+ (so le trong)
+ AD = BC ; AB = CD
Xét và có :
+
+
theo tỉ lệ đồng dạng
Xét có :
EN//CD (gt) mà AB//CD (cmt)
Mà
theo tỉ lệ đồng dạng (Vì
Vậy khẳng định (I), (II), (III) đều đúng.
Bài 10: Cho theo tỉ số 2. Khẳng định nào sau đây là đúng
Vì theo tỉ số 2 (gt)
B. Lý thuyết Hai tam giác đồng dạng
1. Định nghĩa
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
Kí hiệu: (viết theo thứ tự cặp đỉnh tương ứng).
Tỉ số là tỉ số đồng dạng của với .
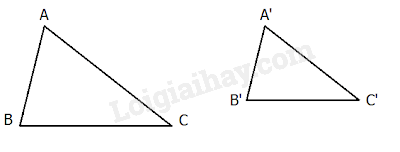
Nhận xét:
- với tỉ số đồng dạng k thì với tỉ số đồng dạng . Ta nói hai tam giác A’B’C’ và ABC đồng dạng với nhau.
- Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng k = 1. Mọi tam giác đồng dạng với chính nó.
- với tỉ số đồng dạng k và với tỉ số đồng dạng m thì với tỉ số đồng dạng k.m.
2. Định lí
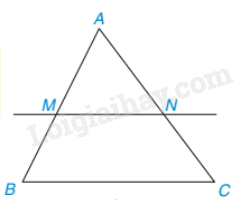
Nếu một đường thẳng cắt hai cạnh của một tam giác là song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
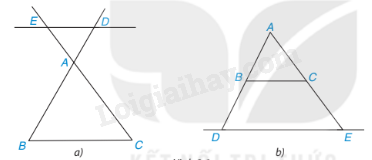
Chú ý. Định lí trên vẫn đúng nếu thay bằng đường thẳng cắt phần kéo dài của hai cạnh tam giác.
Sơ đồ tư duy Hai tam giác đồng dạng
