Giải SBT Toán 8 trang 97 Tập 1 Cánh diều

Nguyễn Mạnh Tài Ngày: 17-11-2023 Lớp 8

790

Với lời giải SBT Toán 8 trang 97 Tập 1 Bài 5: Hình chữ nhật sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 5: Hình chữ nhật

Bài 21 trang 97 SBT Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Hình thang có hai cạnh góc vuông là hình chữ nhật

b) Hình thang cân có một góc vuông là hình chữ nhật

c) Hình bình hành có một góc vuông là hình chữ nhật

d) Tứ giác có hai góc vuông là hình chữ nhật.

Lời giải:

a) Sai

b) Đúng

c) Đúng

d) Sai

Bài 22 trang 97 SBT Toán 8 Tập 1: Hình 20 mô tả mặt phẳng cắt ngang tầng trệt của một ngôi nhà. Biết $A B ⊥ B C, C D ⊥ B C$ và $A B = 4 m, C D = 7 m, A D = 11 m$ . Tính độ dài $B C$ (làm tròn kết quả đến hàng phần mười của mét).

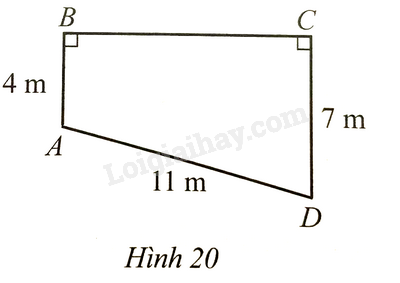
Sách bài tập Toán 8 Bài 5 (Cánh diều): Hình chữ nhật (ảnh 1)

Lời giải:

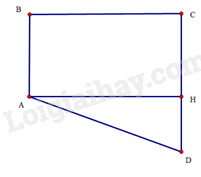
Sách bài tập Toán 8 Bài 5 (Cánh diều): Hình chữ nhật (ảnh 2)

Kẻ $A H$ vuông góc với $C D$ tại $H$ (Hình 42)

Tứ giác $A B C H$ có $\hat{A B C} = \hat{B C H} = \hat{C H A} = 90^{\circ}$ nên $A B C H$ là hình chữ nhật. Suy ra $C H = A B = 4 m$

Do đó $D H = C D - C H = 3 m$

Trong tam giác $A D H$ vuông tại $H$ , ta có:

$A D^{2} = A H^{2} + D H^{2}$

Suy ra $A H^{2} = A D^{2} - D H^{2} = 112$

Do đó $A H = \sqrt{112} m$

Ta có: $B C = A H$ (vì $A B C H$ là hình chữ nhật) nên $B C = \sqrt{112} \approx 10, 6 (m)$

Bài 23 trang 97 SBT Toán 8 Tập 1: Cho hình chữ nhật $A B C D$ có hai đường chéo $A C$ và $B D$ cắt nhau tại $O$ . Lấy điểm $M$ thuộc đoạn thẳng $O C$ . Gọi $E, F$ lần lượt là hình chiếu của điểm $M$ trên đường thẳng $A B, A D$ . Chứng minh:

a) Tứ giác $A E M F$ là hình chữ nhật.

b) $B D / / E F$ .

Lời giải:

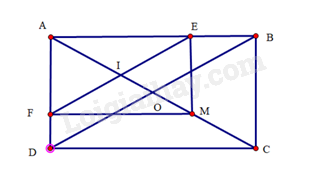
Sách bài tập Toán 8 Bài 5 (Cánh diều): Hình chữ nhật (ảnh 3)

Gọi $I$ là giao điểm của $A M$ và $E F$

a) Tứ giác $A E M F$ có $\hat{F A E} = \hat{A E M} = \hat{M F A} = 90^{\circ}$ nên $A E M F$ là hình chữ nhật.

b) Do $A B C D$ và $A E M F$ là hình chữ nhật nên $O A = O B$ và null. Suy ra tam giác $O A B$ cân tại $O$ và tam giác $I A E$ cân tại $I$ .

Do đó $\hat{O B A} = \hat{O A B}$ và $\hat{I E A} = \hat{I A E}$ hay $\hat{O B A} = \hat{I E A}$ .

Mà $\hat{O B A}$ và $\hat{I E A}$ nằm ở vị trí đòng vị, suy ra $B D / / E F$ .

Bài 24 trang 97 SBT Toán 8 Tập 1: Cho tam giác $A B C$ cân tại $A$ có các đường trung tuyến $B M, C N$ cắt nhau tại $G$ . Trên tia đối của tia $G B, G C$ lần lượt lấy các điểm $D, E$ sao cho $G D = G B, G E = G C$ . Tứ giác $B E D C$ là hình gì? Vì sao?

Lời giải:

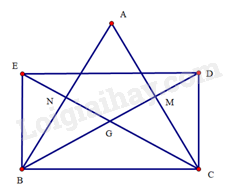
Sách bài tập Toán 8 Bài 5 (Cánh diều): Hình chữ nhật (ảnh 4)

Tứ giác $B E D C$ có hai đường chéo $B D$ và $C E$ cắt nhau tại trung điểm $G$ của mỗi đường nên $B E D C$ là hình bình hành.

Ta có: $A B = A C, A M = C M, A N = B N$ nên $B N = C M$ .

$Δ B C M = Δ C B N$ (c.g.c). Suy ra $B M = C N$ .

Do $G$ là trọng tâm của tam giác $A B C$ nên

$B G = \frac{2}{3} B M$ và $C G = \frac{2}{3} C N$

Do đó $B G = C G$ . Mà $G$ là trung điểm của $B D$ và $C E$ , suy ra $B D = C E$

Hình bình hành $B E D C$ có $B D = C E$ nên $B E D C$ là hình chữ nhật.

Bài 25 trang 97 SBT Toán 8 Tập 1: Cho tam giác $A B C$ vuông cân tại $A$ . Lấy điểm $M$ thuộc cạnh huyền $B C$ . Gọi $D, E$ lần lượt là hình chiếu của điểm $M$ trên đường thẳng $A B, A C$ .

a) Tứ giác $A D M E$ là hình gì? Vì sao?

b) Gọi $I$ là trung điểm của $D E$ . Chứng minh ba điểm $A, I, M$ thẳng hàng

c) Chứng minh khi điểm $M$ thay đổi vị trí trên cạnh $B C$ thì chu vi của tứ giác $A D M E$ không đổi.

Lời giải:

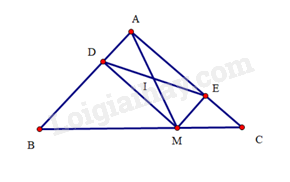
Sách bài tập Toán 8 Bài 5 (Cánh diều): Hình chữ nhật (ảnh 5)

a) Tứ giác $A D M E$ có $\hat{D A E} = \hat{A E M} = \hat{M D A} = 90^{\circ}$ nên $A D M E$ là hình chữ nhật.

b) Do $A D M E$ là hình chữ nhật nên hai đường chéo $D E$ và $A M$ cắt nhau tại trung điểm của mỗi đường.

Mà $I$ là trung điểm của $D E$ , suy ra $I$ là trung điểm của $A M$ . Vậy ba điểm $A < I, M$ thẳng hàng.

c) Do $A D M E$ là hình chữ nhật nên $D M / / A C$ . Suy ra $\hat{B M D} = \hat{A C B}$ (hai góc so le trong). Mà $\hat{A B C} = \hat{A C B} = 45^{\circ}$ (vì tam giác $A B C$ vuông cân tại $A$ , suy ra $\hat{B M D} = \hat{A B C} = 45^{\circ}$ . Do đó, tam giác $B D M$ cân tại $D$ . Suy ra $B D = D M$ .

Chu vi hình chữ nhật $A D M E$ là: $2 (A D + D M) = 2 (A D + B D) = D M$

Mà $A B$ không đổi nên chu vi của tứ giác $A D M E$ không đổi.

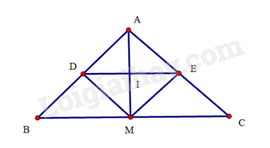
Sách bài tập Toán 8 Bài 5 (Cánh diều): Hình chữ nhật (ảnh 6)

Do $A D M E$ là hình chữ nhật nên $A M = D E$

Suy ra $D E$ có độ dài nhỏ nhất khi $A M$ có độ dài nhỏ nhất. vậy $M$ là hình chiếu của $A$ trên đường thẳng $B C$ .

Trong tam giác $A B C$ vuông cân tại $A$ ta có

$A C = A B = 2 c m$ và $B C^{2} = A B^{2} + A C^{2} = 8$

Suy ra $B C = \sqrt{8} c m$

$Δ A B M = Δ A C M$ (cạnh góc vuông – góc nhọn). Suy ra $B M = C M = \frac{B C}{2} = \sqrt{2} c m$

Tam giác $A B M$ vuông tại $M$ có $\hat{A B M} = 45^{\circ}$ nên $\hat{B A M} = \hat{A B M} = 45^{\circ}$ . Suy ra tam giác $A B M$ vuông cân tại $M$ . Do đó $A M = B M = \sqrt{2} c m$ . Vậy $D E = \sqrt{2} c m$ .