Với giải sách bài tập Toán 7 Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Giải Toán 7 trang 92 Tập 1

Bài 9 trang 92 Toán 7 Tập 1: Trong các hình 18a, 18b, 18c, 18d có hai hình lăng trụ đứng tứ giác. Chỉ ra các hình lăng trụ đứng tứ giác đó?

Lời giải

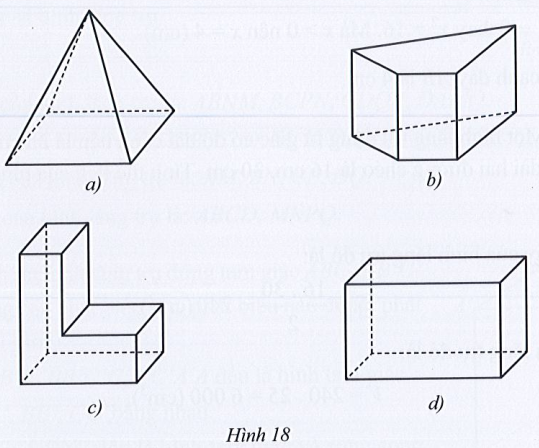
Quan sát Hình 18 ta thấy;

• Hình 18a có một mặt đáy nên không phải là hình lăng trụ đứng tứ giác.

• Hình 18b có 6 mặt (2 mặt đáy cùng là tứ giác và song song với nhau, các mặt bên đều là hình chữ nhật), 12 cạnh, 8 đỉnh nên là hình lăng trụ đứng tứ giác.

• Hình 18c có hai mặt bên không phải là hình tứ giác hoặc hình chữ nhật nên không phải là hình lăng trụ đứng tứ giác.

• Hình 18d là hình hộp chữ nhật nên cũng là hình lăng trụ đứng tứ giác.

Vậy hình 18b, 18d là hình lăng trụ đứng tứ giác.

Bài 10 trang 92 Toán 7 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Hình lăng trụ đứng tam giác có 4 cạnh, 6 đỉnh.

b) Hình lăng trụ đứng tam giác có 5 mặt, 5 đỉnh.

c) Hình lăng trụ đứng tam giác có 4 mặt, 5 đỉnh.

d) Hình lăng trụ đứng tam giác có 5 mặt, 6 đỉnh.

Lời giải

a) Hình lăng trụ đứng tam giác có 4 cạnh, 6 đỉnh là phát biểu sai vì hình lăng trụ đứng tam giác có 9 cạnh, 6 đỉnh.

b) Hình lăng trụ đứng tam giác có 5 mặt, 5 đỉnh là phát biểu sai vì hình lăng trụ đứng tam giác có 5 mặt, 6 đỉnh.

c) Hình lăng trụ đứng tam giác có 4 mặt, 5 đỉnh là phát biểu sai vì hình lăng trụ đứng tam giác có 5 mặt, 6 đỉnh.

d) Hình lăng trụ đứng tam giác có 5 mặt, 6 đỉnh là phát biểu đúng.

Vậy trong các phát biểu trên, phát biểu a, b, c là phát biểu sai; phát biểu d là phát biểu đúng.

Bài 11 trang 92 Toán 7 Tập 1: Cho hình lăng trụ đứng tứ giác ABCD.A'B'C'D'  có đáy là hình thang ABCD vuông tại B (AB song song với CD) với AB = 9 dm, DC = 6 dm, BC = 4 dm, AD = 5 dm và chiều cao AA' = 100 cm (Hình 19).

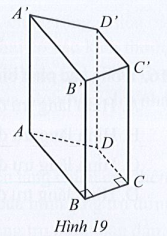
a) Tính diện tích xung quanh của hình lăng trụ ABCD.A'B'C'D'.

b) Tính thể tích của hình lăng trụ ABCD.A'B'C'D'.

c) Người ta dán giấy màu (bên ngoài) tất cả các mặt của hình lăng trụ. Tính số tiền người đó phải trả, biết rằng giá tiền dán giấy màu mỗi mét vuông (bao gồm tiền công và nguyên vật liệu) là 150 000 đồng.

Lời giải

a) Đổi 100 cm = 10 dm.

Chu vi của đáy ABCD của hình lăng trụ là:

9 + 6 + 4 + 5 = 24 (dm).

Diện tích xung quanh của hình lăng trụ ABCD.A'B'C'D' là:

24 . 10 = 240 (dm²).

Vậy diện tích xung quanh của hình lăng trụ ABCD.A'B'C'D' là 240 dm².

b) Diện tích đáy ABCD của hình lăng trụ là:

$\frac{\left(9+6\right).4}{2}$ = 30 (dm²).

Thể tích của hình lăng trụ ABCD.A'B'C'D' là:

30. 10 = 300 (dm³).

Vậy thể tích của hình lăng trụ ABCD.A'B'C'D' là 300 dm³.

c) Tổng diện tích tất cả các mặt của hình lăng trụ là:

240 + 2.30 = 300 (dm²) = 3 (m²).

Số tiền người đó phải trả là:

3. 150 000 = 450 000 (đồng).

Vậy người đó phải trả 450 000 đồng.

Giải Toán 7 trang 93 Tập 1

Bài 12 trang 93 Toán 7 Tập 1: Cho hình lăng trụ đứng tam giác ABC.DEG có đáy là tam giác ABC vuông tại B với cạnh đáy AB = 2 cm và cạnh bên AD = 5 cm (Hình 20). Tính độ dài cạnh BC, biết thể tích của hình lăng trụ đó bằng 25 cm³.

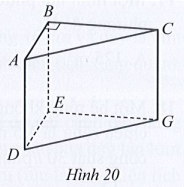
Lời giải

Diện tích đáy ABC của hình lăng trụ là:

25 : 5 = 5 (cm²).

Công thức tính diện tích đáy là tam giác ABC vuông tại B là:

S_ABC = $\frac{1}{2}$AB.BC

Do đó độ dài cạnh BC là:

BC = $\frac{2S_{ABC}}{AB}=\frac{2.5}{2}$ = 5 (cm).

Vậy độ dài cạnh BC là 5 cm.

Bài 13 trang 93 Toán 7 Tập 1: Cho hình lăng trụ đứng tứ giác ABCD.MNPQ có đáy là hình thang ABCD vuông tại B (AD song song với BC) với AB = 20 cm, AD = 11 cm, BC = 15 cm (Hình 21).

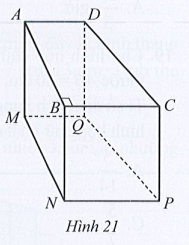
a) Tính tỉ số giữa thể tích của hình lăng trụ đứng tam giác ABC.MNP và thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ.

b) Tính tỉ số phần trăm giữa thể tích của hình lăng trụ đứng tam giác ABD.MNQ và thể tích của hình lăng trụ đứng tam giác BCD.NPQ.

c) So sánh thể tích của hai hình lăng trụ đứng tam giác ABD.MNQ và ACD.MPQ.

Lời giải

a) • Diện tích đáy tam giác ABC vuông tại B là:

S_ABC = $\frac{1}{2}$AB.BC = $\frac{1}{2}$.20.15 = 150 (cm²).

Thể tích của hình lăng trụ đứng tam giác ABC.MNP là:

S_ABC.BN (cm³).

• Diện tích đáy hình thang ABCD vuông tại B là:

S_ABCD = $\frac{1}{2}$(AD + BC).AB = $\frac{1}{2}$.(11 + 15).20 = 260 (cm²).

Thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ là:

S_ABCD.BN (cm³).

Tỉ số giữa thể tích của hình lăng trụ đứng tam giác ABC.MNP và thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ là:

$$\begin{gathered} \frac{V_{ABC.MNP}}{V_{ABCD.MNPQ}}=\frac{S_{ABC}.BN}{S_{ABCD}.BN} \\ =\frac{S_{ABC}}{S_{ABCD}}=\frac{150}{260}=\frac{15}{26}. \end{gathered}$$

Vậy tỉ số cần tìm bằng $\frac{15}{26}$

b) • Diện tích đáy tam giác ABD vuông tại A là:

S_ABD = $\frac{1}{2}$AB.AD = $\frac{1}{2}$.20.11 = 110 (cm²).

Thể tích của hình lăng trụ đứng tam giác ABD.MNQ là:

S_ABD.BN (cm³).

• Diện tích đáy tam giác BCD là:

S_ABCD = $\frac{1}{2}$h_D.BC = $\frac{1}{2}$.AB.BC = $\frac{1}{2}$.20.15 = 150 (cm²).

Thể tích của hình lăng trụ đứng tam giác BCD.NPQ là:

S_BCD.BN (cm³).

Tỉ số phần trăm giữa thể tích của hình lăng trụ đứng tam giác ABD.MNQ và thể tích của hình lăng trụ đứng tam giác BCD.NPQ là:

$\frac{V_{ABD.MNQ}}{V_{BCD.NPQ}}.100\%=\frac{S_{ABD}.BN}{S_{BCD}.BN}.100\%$

$$\begin{gathered} =\frac{S_{ABD}}{S_{BCD}}.100\%=\frac{110}{150}.100\% \\ =73,\left(3\right)\%. \end{gathered}$$

Vậy tỉ số phần trăm cần tìm bằng 73,(3)%.

c) Thể tích của hai hình lăng trụ đứng tam giác ABD.MNQ và ACD.MPQ bằng nhau do diện tích hai đáy ABD, ACD bằng nhau và chúng có cùng chiều cao BN.

Bài 14 trang 93 Toán 7 Tập 1: Sắp xếp các hình sau theo thứ tự thể tích giảm dần:

– Hình lăng trụ đứng tứ giác có độ dài cạnh bên bằng 10 cm và đáy là hình thang cân với độ dài đáy bé, đáy lớn, đường cao lần lượt bằng 2 cm, 8 cm, 4 cm;

– Hình lập phương có độ dài cạnh bằng 8 cm;

– Hình lăng trụ đứng tam giác có độ dài cạnh bên bằng 10 cm và đáy là tam giác có độ dài một cạnh, đường cao tương ứng cạnh đó lần lượt bằng 4 cm, 3 cm.

Lời giải

• Xét hình lăng trụ đứng tứ giác:

Diện tích hình lăng trụ đứng tứ giác là:

$\frac{1}{2}$.(2 + 8).4 = 20 (cm²).

Thể tích của hình lăng trụ đứng tứ giác là:

20.10 = 200 (cm³).

• Xét hình lập phương:

Thể tích của hình lập phương là:

8³ = 512 (cm³).

• Xét hình lăng trụ đứng tam giác:

Diện tích đáy tam giác là:

$\frac{1}{2}$.4.3 = 6 (cm²).

Thể tích của hình lăng trụ đứng tam giác là:

6.10 = 60 (cm³).

Do 512 > 200 > 60 nên sắp xếp các hình theo thứ tự thể tích giảm dần là: hình lập phương, hình lăng trụ đứng tứ giác, hình lăng trụ đứng tam giác.

Bài 15* trang 93 Toán 7 Tập 1: Người ta ghi một cách tuỳ ý vào ba mặt bên và hai mặt đáy của hình lăng trụ đứng tam giác các số tự nhiên lẻ từ 21 đến 29 (số được ghi ở mỗi mặt khác nhau). Chứng tỏ rằng không thể xảy ra trường hợp tổng các số trên ba mặt bên và tổng các số trên hai đáy của hình lăng trụ trên bằng nhau.

Lời giải

Do tổng của ba số lẻ là một số lẻ nên tổng các số trên ba mặt bên của hình lăng trụ là một số lẻ.

Mà tổng của hai số lẻ là một số chẵn nên tổng các số trên hai đáy của hình lăng trụ là một số chẵn.

Do đó không thể xảy ra trường hợp tổng các số trên ba mặt bên và tổng các số trên hai đáy của hình lăng trụ trên bằng nhau.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 1: Hình hộp chữ nhật. Hình lập phương

Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Bài ôn tập chương 3

Bài 1 : Góc ở vị trí đặc biệt

Bài 2 : Tia phân giác của một góc

Lý thuyết Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

1. Hình lăng trụ đứng tam giác

- Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.

- Hai mặt đáy cùng là tam giác và nằm trong hai mặt phẳng song song với nhau; Mỗi mặt bên là hình chữ nhật;

- Các cạnh bên bằng nhau;

- Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.

Ví dụ:

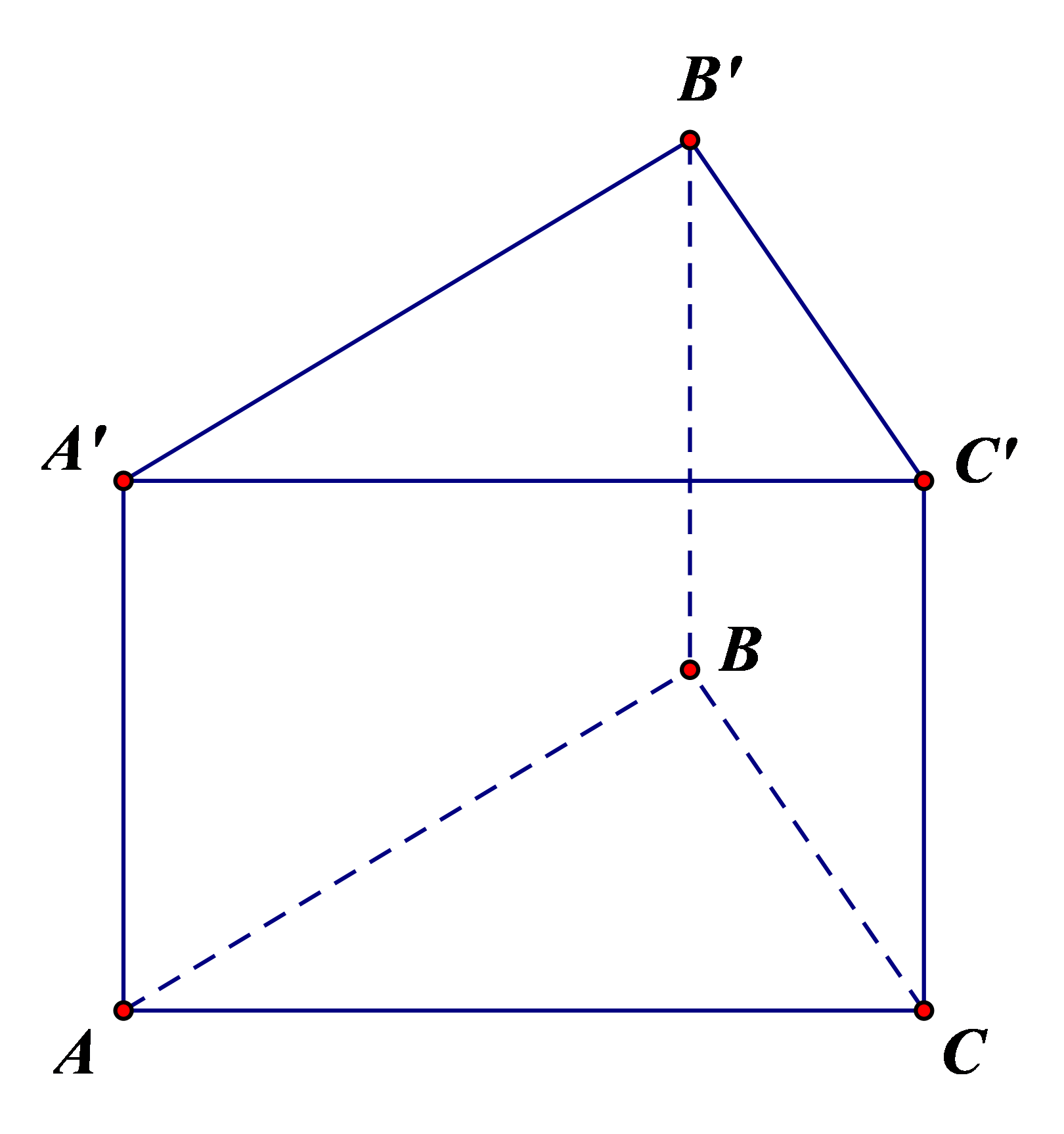
Hình lăng trụ đứng tam giác ABC.A'B'C' có:

- Đáy dưới là tam giác ABC, đáy trên là tam giác A'B'C';

Các mặt bên là các hình chữ nhật: AA'B'B, BB'C'C, CC'A'A;

- Các cạnh:

+ Cạnh đáy: AB, BC, CA, A'B', B'C', C'A'

+ Cạnh bên: AA', BB', CC';

- Các đỉnh: A, B, C, A', B', C'.

- Chiều cao là độ dài một cạnh bên: AA' hoặc BB' hoặc CC'.

2. Hình lăng trụ đứng tứ giác

- Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.

- Hai mặt đáy cùng là tứ giác và song song với nhau. Mỗi mặt bên là hình chữ nhật.

- Các cạnh bên bằng nhau.

- Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên.

Ví dụ:

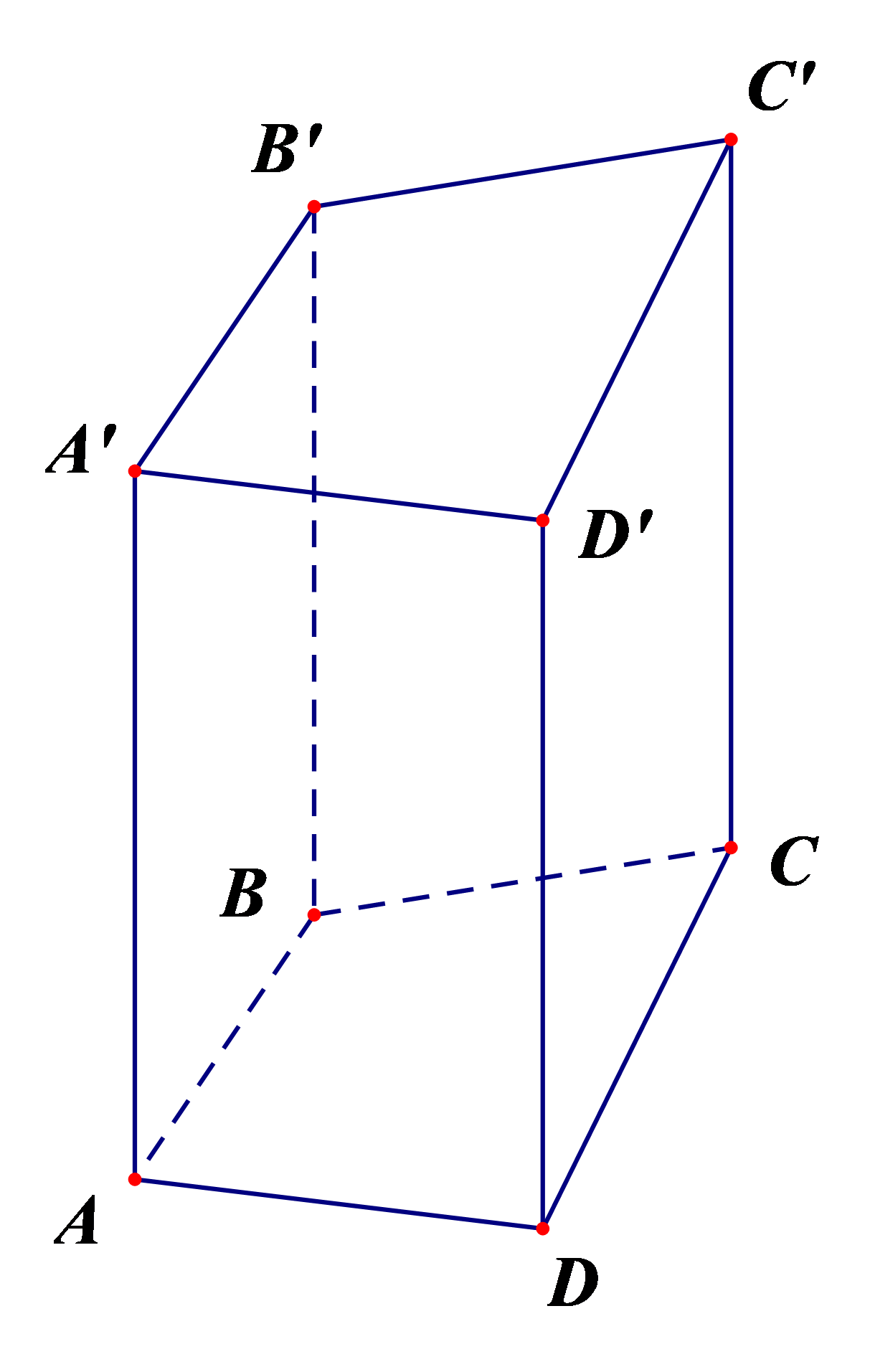
Hình lăng trụ đứng tứ giác ABCD.A'B'C'D' có:

- Đáy dưới là tứ giác ABCD, đáy trên là tứ giác A'B'C'D';

Các mặt bên là các hình chữ nhật:  AA'B'B, BB'C'C, CC'D'D, DD'A'A;

- Các cạnh:

+ Cạnh đáy: AB, BC, CD, DA, A'B', B'C', C'D', D'A'

+ Các cạnh bên: AA', BB', CC', DD' bằng nhau.

- Các đỉnh: A, B, C, D, A', B', C', D'.

- Chiều cao là độ dài một cạnh bên: AA' hoặc BB' hoặc CC' hoặc DD'.

Chú ý: Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác.

3. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

- Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.

Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác.

- Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.

Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác.

- Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.

Tức là S_xq = C . h, trong đó S_xq là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.

Ví dụ:

a) Cho hình lăng trụ đứng tam giác ABC.A'B'C'.

S_xq  = C . h, trong đó C là chu vi của tam giác ABC (hoặc tam giác A'B'C'), h là độ dài cạnh bên AA' (hoặc BB, hoặc CC').

V = S . h, trong đó S là diện tích tam giác ABC (hoặc A'B'C'), h là độ dài cạnh bên AA' (hoặc BB' hoặc CC').

b) Cho hình lăng trụ đứng tứ giác ABCD.A'B'C'D':

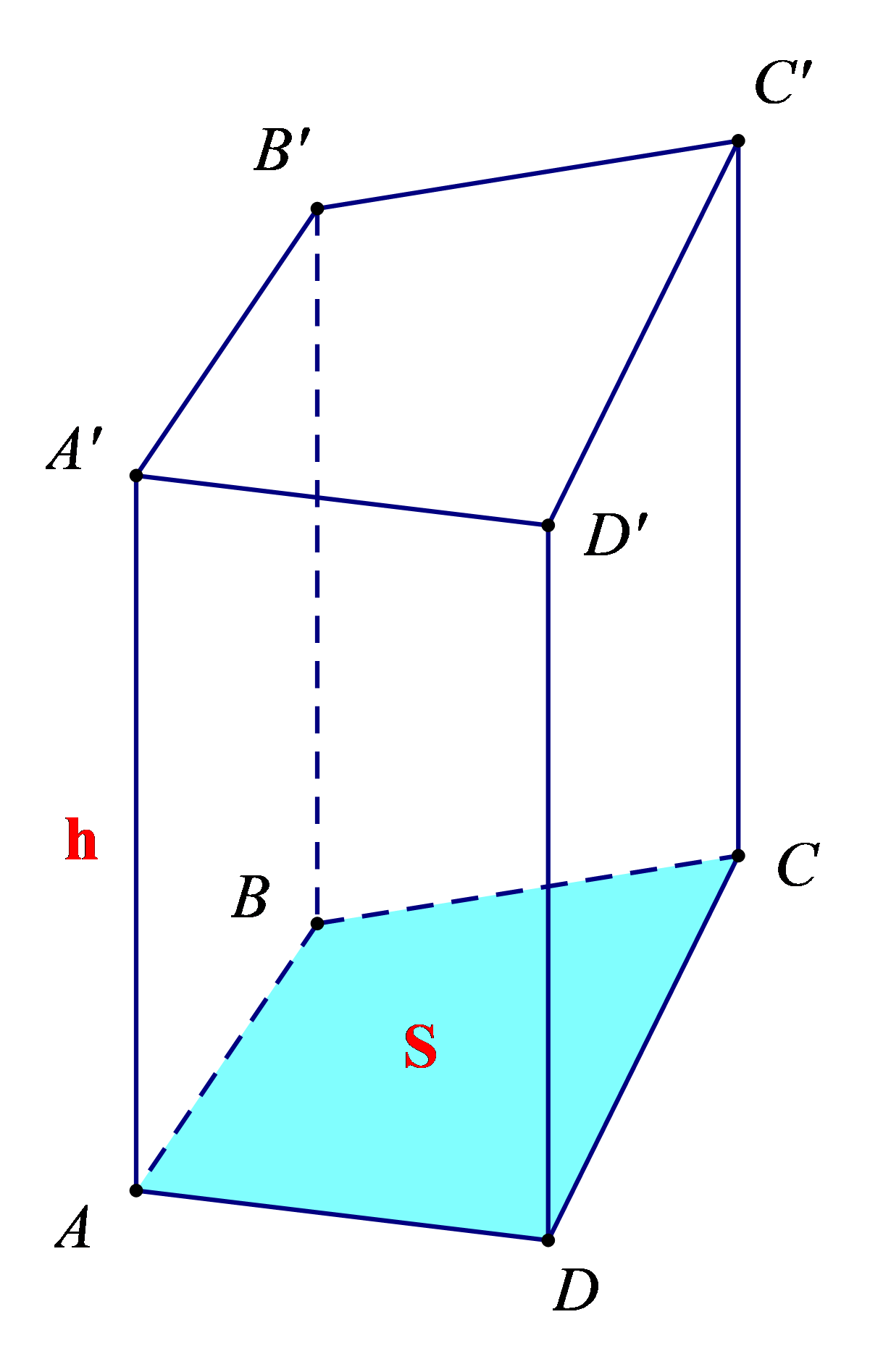
S_xq  = C . h, trong đó C là chu vi của tứ giác ABCD (hoặc tứ giác A'B'C'D'), h là độ dài cạnh bên AA' (hoặc BB, hoặc CC', hoặc DD').

V = S . h, trong đó S là diện tích tứ giác ABCD (hoặc A'B'C'D'), h là độ dài cạnh bên AA' (hoặc BB' hoặc CC', hoặc DD').