Với giải sách bài tập Toán 7 Bài 1: Hình hộp chữ nhật. Hình lập phương sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 1: Hình hộp chữ nhật. Hình lập phương

Giải Toán 7 trang 87 Tập 1

Bài 1 trang 87 Toán 7 Tập 1:

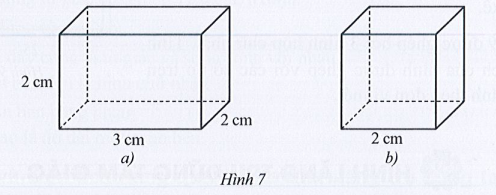
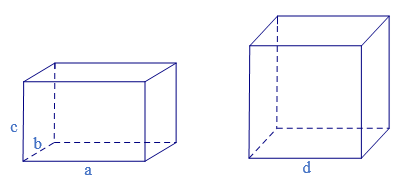
a) Tính thể tích và diện tích xung quanh của hình hộp chữ nhật ở Hình 7a.

b) Tính thể tích và diện tích xung quanh của hình lập phương ở Hình 7b.

Lời giải

– Hình 7a:

Hình hộp chữ nhật có ba kích thước: chiều dài là a, chiều rộng là b, chiều cao là c (a, b, c cùng đơn vị đo).

Công thức tính thể tích của hình hộp chữ nhật trên là:

V = abc (đơn vị thể tích).

Công thức tính diện tích xung quanh của hình hộp chữ nhật trên là:

S_xq = 2(a + b)c (đơn vị diện tích).

Do đó:

Thể tích của hình hộp chữ nhật này là:

V = 3.2.2 = 12 (cm³).

Diện tích xung quanh của hình hộp chữ nhật này là:

S_xq = 2.(3 + 2).2 = 20 (cm²).

Vậy V = 12 cm³ và S_xq = 20 cm².

– Hình 7b:

Hình lập phương có độ độ dài cạnh là d.

Công thức tính thể tích của hình lập phương trên là:

V = d³ (đơn vị thể tích).

Công thức tính diện tích xung quanh của hình lập phương trên là:

S_xq = 4d² (đơn vị diện tích).

Do đó:

Thể tích của hình hộp chữ nhật này là:

V = 2³ = 8 (cm³).

Diện tích xung quanh của hình hộp chữ nhật này là:

S_xq = 4.2² = 16 (cm²).

Vậy V = 8 cm³ và S_xq = 16 cm².

Bài 2 trang 87 Toán 7 Tập 1: Tính độ dài cạnh của hình lập phương, biết thể tích của hình lập phương đó bằng thể tích của hình hộp chữ nhật có ba kích thước: chiều dài là 8 dm, chiều rộng là 4 dm, chiều cao là 2 dm.

Lời giải

Thể tích của hình hộp chữ nhật có ba kích thước chiều dài là 8 dm, chiều rộng là 4 dm, chiều cao là 2 dm là:

8.4.2 = 64 (dm³).

Gọi d (dm) (d > 0) là độ dài cạnh của hình lập phương.

Khi đó thể tích của hình lập phương là: d³ (dm³).

Do thể tích của hình lập phương bằng thể tích của hình hộp chữ nhật trên nên ta có:

d³ = 64.

Suy ra d³ = 4³

Do đó d = 4 (dm).

Vậy độ dài cạnh của hình lập phương là 4 dm.

Bài 3 trang 87 Toán 7 Tập 1: Người ta xếp các hình lập phương có độ dài cạnh là 2 cm để được một hình hộp chữ nhật có ba kích thước: chiều dài là 12 cm, chiều rộng là 8 cm, chiều cao là 10 cm. Hỏi phải dùng tất cả bao nhiêu hình lập phương để xếp được hình hộp chữ nhật đó?

Lời giải

Thể tích của hình hộp chữ nhật có ba kích thước chiều dài là 12 cm, chiều rộng là 8 cm, chiều cao là 10 cm là:

12.8.10 = 960 (cm³).

Thể tích của hình lập phương có độ dài cạnh là 2 cm là:

2³ = 8 (cm³).

Số hình lập phương phải dùng tất cả để xếp được hình hộp chữ nhật đó là:

960 : 8 = 120 (hình).

Vậy phải dùng tất cả 120 hình lập phương để xếp được hình hộp chữ nhật đó.

Bài 4 trang 87 Toán 7 Tập 1: Cho hình hộp chữ nhật ABCD.A'B'C'D' (Hình 8). Diện tích của các mặt ABCD, BB'C'C và CC'D'D lần lượt là 2 cm², 6 cm², 3 cm². Tính thể tích hình hộp chữ nhật ABCD.A'B'C'D'.

Lời giải

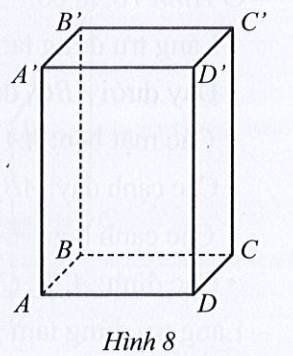
Gọi các kích thước của hình hộp chữ nhật ABCD.A'B'C'D' như sau: AB = a (cm), AD = b (cm), AA' = c (cm) (a > 0, b > 0, c > 0).

Khi đó thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là: V = abc (cm³).

• Diện tích của mặt ABCD là:

S_ABCD = ab (cm²)

Mà theo bài S_ABCD = 2 cm².

Do đó ab = 2.

Tương tự ta có:

• S_BB'C'C = bc = 6 (cm²). Do đó bc = 6.

• S_CC'D'D = ac = 3 (cm²). Do đó ac = 3.

Suy ra: (ab).(bc).(ac) = 2.6.3

Hay a²b²c² = 36

Suy ra (abc)² = 6²

Do đó abc = 6.

Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là 6 cm³.

Giải Toán 7 trang 88 Tập 1

Bài 5 trang 88 Toán 7 Tập 1: Một bể rỗng không chứa nước có dạng hình hộp chữ nhật với chiều dài là 2,2 m, chiều rộng là 1 m, chiều cao là 0,75 m. Người ta sử dụng một máy bơm nước có công suất 25 lít/phút để bơm đây bể đó. Hỏi sau bao nhiêu giờ thì bể đầy nước?

Lời giải

Thể tích của bể chính là thể tích của hình hộp chữ nhật có chiều dài là 2,2 m, chiều rộng là 1 m, chiều cao là 0,75 m.

Do đó thể tích của bể đó là:

2,2.1.0,75 = 1,65 (m³) = 1 650 (l).

Người ta sử dụng một máy bơm nước có công suất 25 lít/phút để bơm đây bể đó nên cứ một phút bể bơm được 25 lít nước.

Thời gian để bể đầy nước là:

1 650 : 25 = 66 (phút) = 1,1 (giờ).

Vậy sau 1,1 giờ thì bể đầy nước.

Bài 6 trang 88 Toán 7 Tập 1: Một căn phòng có dạng hình hộp chữ nhật với chiều dài là 5 m, chiều rộng là 3,2 m, chiều cao là 3 m. Người ta muốn sơn phía trong bốn bức tường và cả trần của căn phòng. Tính số tiền mà người đó phải trả, biết rằng diện tích các cửa của căn phòng đó là 7 m² và giá tiền sơn mỗi mét vuông (bao gồm tiền công và nguyên vật liệu) là 10 500 đồng.

Lời giải

Diện tích xung quanh hay diện tích bốn bức tường kể cả các cửa của căn phòng (diện tích xung quanh của hình hộp chữ nhật) là:

2. (5 + 3,2). 3 = 49,2 (m²).

Diện tích trần của căn phòng (diện tích mặt đáy hình hộp chữ nhật) là:

5.3,2 = 16 (m²).

Diện tích cần quét sơn của căn phòng là:

49,2 + 16 – 7 = 58,2 (m²).

Số tiền người đó phải trả để quét sơn căn phòng là:

58,2 . 10 500 = 611 100 (đồng).

Vậy người đó cần phải trả để quét sơn là 611 100 đồng.

Bài 7 trang 88 Toán 7 Tập 1: Một bể bơi có dạng hình hộp chữ nhật với chiều dài là 12 m, chiều rộng là 5 m, chiều sâu là 1,75 m. Người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh bể đó? Biết rằng mỗi viên gạch có dạng hình chữ nhật với chiều dài là 25 cm, chiều rộng là 20 cm và diện tích mạch vữa không đáng kể.

Lời giải

Diện tích đáy bể dạng hình hộp chữ nhật là:

12.5 = 60 (m²).

Diện tích xung quanh bể dạng hình hộp chữ nhật là:

2. (12 + 5). 1,75 = 59,5 (m²).

Diện tích cần lát gạch men là:

60 + 59,5 = 119,5 (m²).

Diện tích của mỗi viên gạch men là:

25.20 = 500 (cm²) = 0,05 (m²).

Số viên gạch men mà người thợ phải dùng để lát đáy và xung quanh thành bể đó là:

119,5 : 0,05 = 2 390 (viên).

Vậy người thợ phải dùng 2 390 viên gạch men để lát đáy và xung quanh bể đó.

Bài 8 trang 88 Toán 7 Tập 1: Hình 9 được ghép bởi 3 hình hộp chữ nhật. Tính thể tích của hình được ghép với các số đo trên hình tính theo đơn vị mét.

Lời giải

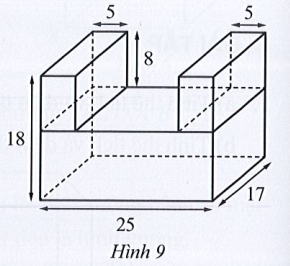
Hình 9 được ghép bởi:

–  Hai hình hộp chữ nhật nhỏ có chiều dài 17 m, chiều rộng 5 m và chiều cao 8 m;

• Thể tích của mỗi hình hộp chữ nhật nhỏ là:

17.5.8 = 680 (m³).

• Thể tích của hai hình hộp chữ nhật nhỏ là:

2.680 = 1 360 (m³).

– Một hình hộp chữ nhật lớn có chiều dài 25 m, chiều rộng 17 m và chiều cao 10 m.

• Thể tích của hình hộp chữ nhật lớn này là:

25.17.10 = 4 250 (m³).

Do đó thể tích của hình được ghép là:

1 360 + 4 250 = 5 610 (m³).

Vậy thể tích của hình được ghép là 5 610 m³.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 2

Bài 1: Hình hộp chữ nhật. Hình lập phương

Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Bài ôn tập chương 3

Bài 1 : Góc ở vị trí đặc biệt

Lý thuyết Hình hộp chữ nhật. Hình lập phương

1. Hình hộp chữ nhật

- Hình hộp chữ nhật có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.

- Các mặt đều là hình chữ nhật.

- Các cạnh bên bằng nhau.

Chú ý: Để nhận dạng tốt hơn hình hộp chữ nhật, người ta vẽ các cạnh không nhìn thấy bằng nét đứt.

Ví dụ:

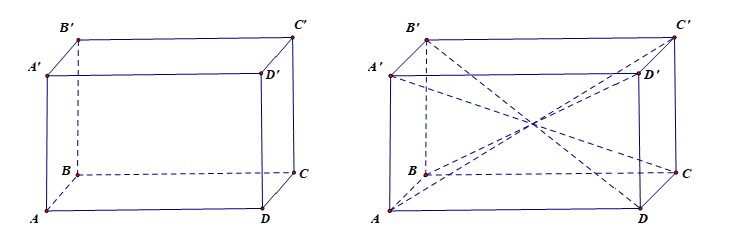
Hình hộp chữ nhật ABCD.A'B'C'D':

- Có 6 mặt đều là hình chữ nhật gồm hai mặt đáy và bốn mặt bên là:

+ Đáy dưới: ABCD, đáy trên A'B'C'D';

+ Mặt bên: AA'B'B, BB'C'C, CC'D'D, DD'A'A;

- Có 12 cạnh gồm 8 cạnh đáy và 4 cạnh bên:

+ Các cạnh đáy là: AB, BC, CD, DA, A'B', B'C', C'D', D'A';

+ Các cạnh bên: AA', BB', CC', DD' đều bằng nhau.

- Có 8 đỉnh: A, B, C, D, A', B', C', D'.

- Có 4 đường chéo: A'C, B'D, C'A, D'B.

2. Hình lập phương

- Hình lập phương có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.

- Các mặt đều là hình vuông.

- Các cạnh đều bằng nhau.

Ví dụ: Hình lập phương ABCD.A'B'C'D'

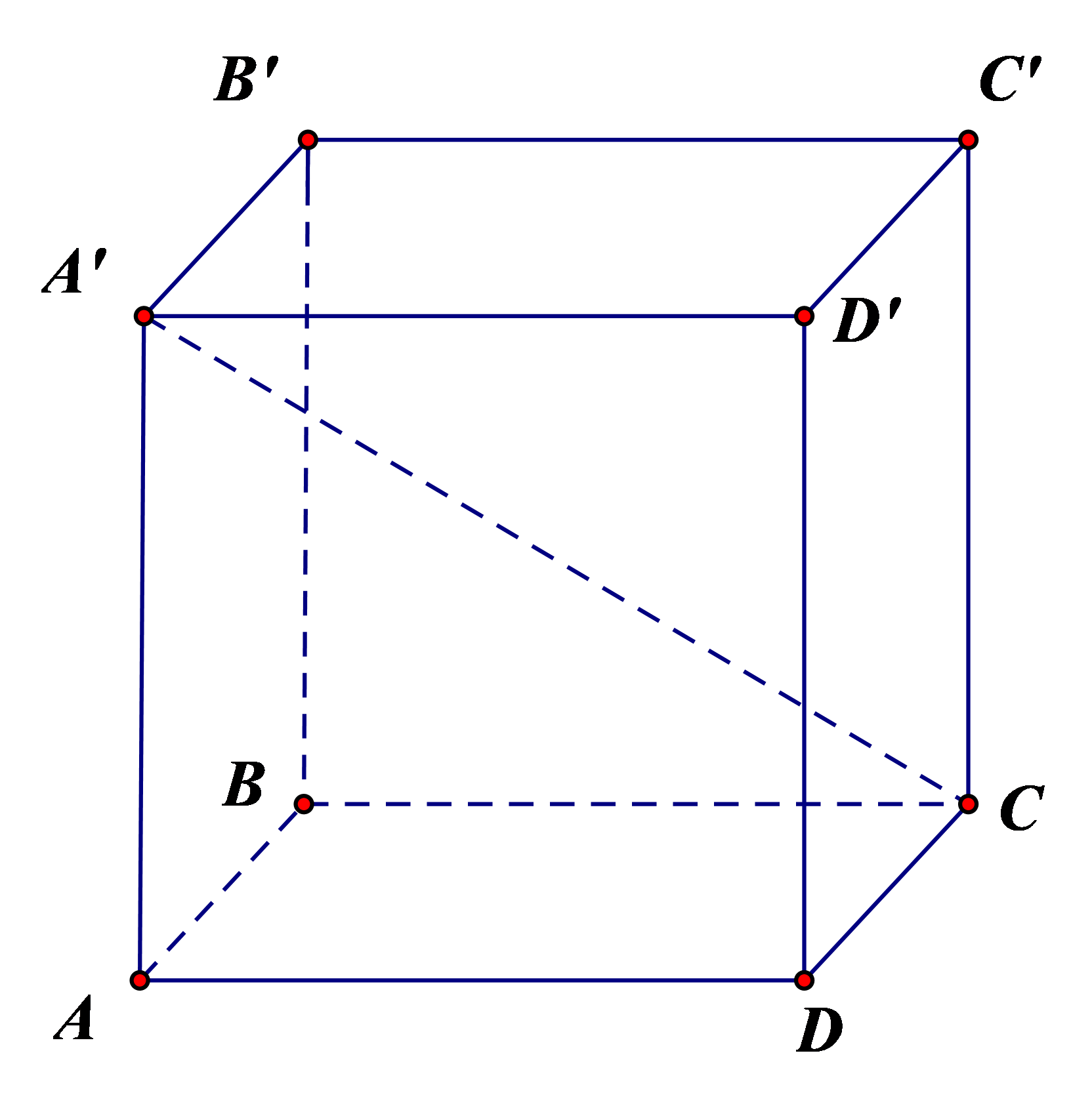
- Có 6 mặt đều là hình vuông, gồm hai đáy và hai mặt bên là:

+ Đáy dưới: ABCD, đáy trên A'B'C'D';

+ Mặt bên: AA'B'B, BB'C'C, CC'D'D, DD'A'A;

- Có 12 cạnh bằng nhau, gồm 8 cạnh đáy và 4 cạnh bên:

+ Các cạnh đáy là: AB, BC, CD, DA, A'B', B'C', C'D', D'A';

+ Các cạnh bên:  AA', BB', CC', DD'.

- Có 8 đỉnh: A, B, C, D, A', B', C', D'.

- Có 4 đường chéo: A'C, B'D, C'A, D'B.

3. Diện tích xung quanh và thể tích của hình hộp chữ nhật và hình lập phương

Cho hình hộp chữ nhật có ba kích thước: chiều dài a, chiều rộng là b, chiều cao là c (a, b, c cùng đơn vị đo). Cho hình lập phương có độ dài cạnh là d.

Ta có một số công thức sau:

Ví dụ:

a) Cho hình hộp chữ nhật có chiều dài 20 m, chiều rộng 7 m, chiều cao 10 m. Tính diện tích xung quanh và thể tích của hình hộp chữ nhật đó.

b) Cho hình lập phương có cạnh là 5 m. Tính diện tích xung quanh và thể tích của hình lập phương đó.

Hướng dẫn giải

a) Áp dụng công thức tính S_xq và thể tích của hình hộp chữ nhật, ta có:

- Diện tích xung quanh của hình hộp chữ nhật là: S_xq = 2.(20 + 7) . 10 = 540 (m²).

- Thể tích của hình hộp chữ nhật là:  V = 20 .7 . 10 = 1400 (m³).

b) Áp dụng công thức tính S_xq và thể tích của hình lập phương, ta có:

- Diện tích xung quanh của hình lập phương là: S_xq = 4 . 5² = 100 (m²).

- Thể tích của hình lập phương là: V = 5³ = 125 (m³).