Với giải sách bài tập Toán 11 Bài 2: Biến cố hợp và quy tắc cộng xác suất sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 2: Biến cố hợp và quy tắc cộng xác suất
a) Gặp ngẫu nhiên 1 đoàn viên trong cuộc gặp mặt, tính xác suất của biến cố “Đoàn viên được gặp đến từ miền Nam hoặc miền Trung”.
b) Gặp ngẫu nhiên 2 đoàn viên trong cuộc gặp mặt, tính xác suất của biến cố “Hai đoàn viên được gặp cùng đến từ miền Bắc hoặc cùng đến từ miền Nam”.
Lời giải:
a) Không gian mẫu của phép thử là .
Xác suất của biến cố “Đoàn viên được gặp đến từ miền Nam” là .
Xác suất của biến cố “Đoàn viên được gặp đến từ miền Trung” là .
Xác suất của biến cố “Đoàn viên được gặp đến từ miền Nam hoặc miền Trung” là: .
b) Không gian mẫu của phép thử là
Số trường hợp xảy ra của biến cố “ Hai đoàn viên được gặp cùng đến từ miền Bắc” là .
Xác suất của biến cố “ Hai đoàn viên được gặp cùng đến từ miền Bắc” là .
Số trường hợp xảy ra của biến cố “ Hai đoàn viên được gặp cùng đến từ miền Nam” là .
Xác suất của biến cố “ Hai đoàn viên được gặp cùng đến từ miền Nam” là .
Xác suất của biến cố “Hai đoàn viên được gặp cùng đến từ miền Bắc hoặc cùng đến từ miền Nam” là .
a) “Cả 3 viên bi lấy ra đều có cùng màu”.
b) “Có không quá 1 viên bi xanh trong 3 viên bi lấy ra”.
c) “Có đúng 2 màu trong 3 viên bi lấy ra”.
Lời giải:
a) Không gian mẫu của phép thử là
Số trường hợp xảy ra của biến cố “Cả 3 viên bi lấy ra đều có màu đỏ” là .
Xác suất của biến cố “Cả 3 viên bi lấy ra đều có màu đỏ” là .
Số trường hợp xảy ra của biến cố “Cả 3 viên bi lấy ra đều có màu đỏ” là .
Xác suất của biến cố “Cả 3 viên bi lấy ra đều có màu vàng” là .
Xác suất của biến cố “Cả 3 viên bi lấy ra đều có cùng màu” là .
b) Số trường hợp xảy ra của biến cố “Không có viên bi xanh nào được lấy ra” là .
Xác suất của biến cố “Không có viên bi xanh nào được lấy ra” là
.
Số trường hợp xảy ra của biến cố “Không có viên bi xanh nào được lấy ra” là .
Xác suất của biến cố “Chỉ có một viên bi xanh được lấy ra” là .
Xác suất của biến cố “Có không quá 1 viên bi xanh trong 3 viên bi lấy ra” là .
c) Gọi A là biến cố “Có đúng 2 màu trong 3 viên bi lấy ra”; B là biến cố “Cả 3 viên bi lấy ra có cùng màu” và C là biến cố “3 viên bi lấy ra có cả 3 màu”.
Ta thấy . Khi đó: ;
Số trường hợp xảy ra của biến cố C là .
.
Do B và C là hai biến cố xung khắc nên
.
Vậy xác suất của biến cố “Có đúng 2 màu trong 3 viên bi lấy ra” là .
Lời giải:
Không gian mẫu của phép thử là (số).
Gọi B là biến cố “Số tạo thành chia hết cho 2”, C là biến cố “Số tạo thành chia hết cho 3”.
Do đó, BC là biến cố “Số tạo thành chia hết cho 6”.
Biến cố B xảy ra khi chữ số hàng đơn vị của số tạo thành là 4, có thể xếp được số chia hết cho 2 nên .
Biến cố B xảy ra khi 3 chữ số của số tạo thành là 1, 4, 7, có thể xếp được số chia hết cho 3 nên .
Có thể tạo thành 2 số chia hết cho 6 là 714 và 174 nên .
Vậy.
Bài 4 trang 100 SBT Toán 11 Tập 2: Cho A và B là hai biến cố độc lập với nhau.
a) Biết P(A) = 0,4 và P() = 0,3. Tính xác suất của các biến cố B và .
b) Biết P() = 0,4 và P() = 0,9. Tính xác suất của các biến cố A, B và AB.
Lời giải:
Vì A và B là hai biến cố độc lập nên và B; A và ; và cũng độc lập.
a) Ta có .
• và B độc lập nên .
•A và B độc lập nên
.
b) Vì và B độc lập nên
Hay .
Khi đó
.
Với; .
Lời giải:
Không gian mẫu của phép thử là .
Sơ đồ hình cây số trường hợp của các biến cố:
Khi đó, xác suất của biến cố “Có ít nhất 3 quả bóng xanh trong 5 quả bóng lấy ra” là: .
Vậy xác suất của biến cố “Có ít nhất 3 quả bóng xanh trong 5 quả bóng lấy ra” là
Lời giải:
Sơ đồ hình cây:
Xác suất của biến cố “Châu phải gieo không quá 3 lần để xuất hiện mặt 6 chấm” là:
.
Vậy xác suất của biến cố “Châu phải gieo không quá 3 lần để xuất hiện mặt 6 chấm” là .
A: “Không có số may mắn nào trong 5 số Dương đã chọn”;
B: “Có đúng 1 số may mắn trong 5 số Dương đã chọn”.
Lời giải:
Không gian mẫu của phép thử là
Biến cố A xảy ra khi 3 số may mắn nằm trong 95 số mà Dương không chọn. Số trường hợp xảy ra của biến cố A là .
Do đó xác suất của biến cố A là: .
Biến cố B xảy ra khi trong 3 số may mắn, có 1 số Dương đã chọn, 2 số còn lại nằm trong 95 số mà Dương không chọn. Số trường hợp xảy ra của biến cố B là .
Do đó, xác suất của biến cố B là: .
Lời giải:
Gọi n là số quả bóng đỏ trong hộp. Tổng số quả bóng trong hộp là n+3 quả.
Không gian mẫu của phép thử là
Số trường hợp xảy ra của biến cố “Lấy được 2 quả bóng xanh” là .
Xác suất lấy được 2 quả bóng xanh là .
Số trường hợp xảy ra của biến cố “Lấy được 2 quả bóng đỏ” là .
Xác suất lấy được 2 quả bóng đỏ là .
Theo đề bài, ta có:
(chọn) hoặc n = 5 (loại).
Khi đó, xác suất của biến cố “Lấy được 2 quả bóng có cùng màu” là
.
Vậy xác suất của biến cố “Lấy được 2 quả bóng có cùng màu” là 0,5.
Lời giải:
Gọi B là biến cố “Tích số chấm xuất hiện trên mỗi con xúc xắc không chia hết cho 5”, C là biến cố “Tích số chấm xuất hiện trên mỗi con xúc xắc không chia hết cho 3”.
Khi đó A là biến cố đối của biến cố .
• Các số chấm không chia hết cho 5 là 1, 2, 3, 4, 6 nên .
• Các số chấm không chia hết cho 3 là 1, 2, 4, 5 nên .
• Các số chấm không chia hết cho 3 và 5 là 1, 2, 4 nên .
Ta có
.
Do đó xác suất của biến cố A là
a) “Tổng các số ghi trên 2 thẻ lấy ra nhỏ hơn 4 hoặc lớn hơn 76”;
b) “Tích các số ghi trên 2 thẻ lấy ra chia hết cho 10”.
Lời giải:
a) Gọi A là biến cố “Tổng các số ghi trên 2 thẻ lấy ra nhỏ hơn 4 hoặc lớn hơn 76”. A1 là biến cố “Tổng các số ghi trên 2 thẻ lấy ra nhỏ hơn 4” và A2 là biến cố “Tổng các số ghi trên 2 thẻ lấy ra lớn hơn 76”.
Khi đó .
Không gian mẫu của phép thử là .
Biến cố A1 xảy ra khi 2 tấm thẻ được chọn ghi số 1 và 2. Do đó số trường hợp xảy ra của biến cố A1 là 1. Từ đó
.
Biến cố A2 xảy ra khi 2 tấm thẻ được chọn ghi số 37 và 40; 38 và 40; 39 và 40; 38 và 39. Do đó số trường hợp xảy ra của biến cố A2 là 4. Từ đó .
Do A1 và A2 là hai biến cố xung khắc nên
.
b) Gọi B là biến cố “Tích các số ghi trên 2 thẻ lấy ra chia hết cho 10”, B1 là biến cố “Tích các số ghi trên 2 thẻ lấy ra không chia hết cho 5” và B2 là biến cố “Tích các số ghi trên 2 thẻ lấy ra không chia hết cho 2”.
Khi đó B là biến cố đối của .
Từ 1 đến 40 có 8 số chia hết cho 5 và 32 số không chia hết cho 5 nên
Từ 1 đến 40 có 20 số chia hết cho 2 và 20 số không chia hết cho 2 nên
.
Từ 1 đến 40 có 4 số chia hết cho 10 nên số các số không chia hết cho 2 và 5 là số. Từ đó ta có
.
Ta có
.
Vậy xác suất của biến cố B “Tích các số ghi trên 2 thẻ lấy ra chia hết cho 10” là
Xem thêm các bài giải SBT Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Khoảng cách trong không gian
Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 1: Biến cố giao và quy tắc nhân xác suất
Bài 2: Biến cố hợp và quy tắc cộng xác suất
Lý thuyết Biến cố hợp và quy tắc cộng xác suất
1. Biến cố hợp
Cho hai biến cố A và B. Biến cố: “A hoặc B xảy ra”, kí hiệu là được gọi là biến cố hợp của A và B.
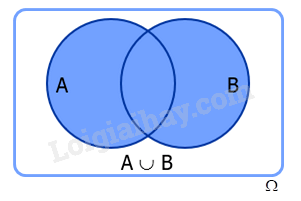
Chú ý: Biến cố xảy ra khi có ít nhất một trong hai biến cố A và B xảy ra. Tập hợp mô tả biến cố là hợp của hai tập hợp mô tả biến cố A và biến cố B.
2. Công thức cộng xác suất
Quy tắc cộng cho hai biến cố xung khắc:
Cho hai biến cố xung khắc A và B. Khi đó .
Quy tắc cộng cho hai biến cố bất kì:
Cho hai biến cố A và B. Khi đó .